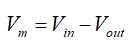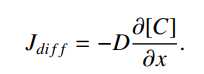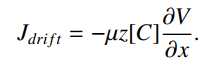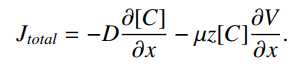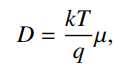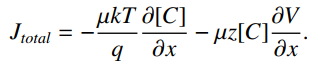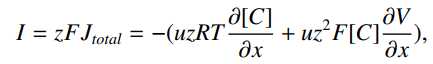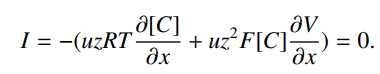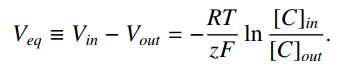计算神经科学（二）

神经元的生物物理特性（一）

神经元或脑细胞与体内的其他细胞相似，两者均具有细胞核、都能够进行细胞的基本活动、都有细胞膜将周围液体和细胞隔开。细胞膜内外的离子浓度不同， 根据热力学理论可知膜电位差会引起离子浓度内外差，反之离子浓度差也会造成膜电位差，这样就建立了一个平衡状态。 因此，对于神经元细胞来说，膜内部和外部之间的每种离子的浓度差产生其独立的平衡能斯特势能。

然而，与体细胞相比神经元最大的不同在于其具体很多离子通道，这些离子通道由特定的蛋白质受体组成。除了允许被动流动的离子通道外，还有一种称为离子泵的门，它主动将离子从一侧传输到另一侧。不同的离子同时影响着膜电压的变化，这导致通过被动和主动运输的所有离子流中的电势处于动态平衡状态。动态平衡状态下的膜电压称为静息电位，约为-65mV。霍奇金和赫胥黎通过研究特定离子流的动力学揭示了动作电位的产生机制。动作电位，即所谓神经元活动的spike。Spike作为信息单元起着重要作用，用于通过突触与相邻神经元的通信。神经网络特定通路中的通信在“生命世界”中产生各种行为，形成简单动物的反射行为，达到了人类的高级认知行为。

静息电位

所有神经元细胞在其细胞膜的内部和外部之间均具有电势差。 静息电位是指细胞处于静止状态下跨膜的电位。

其中Vin是细胞内部的电位，而Vout是外部电位（之后，我使用V来表示膜电压而非Vm）。神经元和其他可兴奋细胞与体内大多数细胞的区别在于，这种静息膜电位可以改变，因此可以作为信号传导机制。例如，典型的神经元具有约-65毫伏的静息电位。向内电流对应于进入电池的带正电荷的离子，例如Na +。 这提高了膜电压；也就是说，它使膜电位更接近于零。 这种情况，我们称之为细胞是去极化的。 向外的电流对应于带正电的离子，例如K +离开细胞或带负电的离子（例如Cl-）进入细胞，这种情况，我们称之为细胞的超极化。

细胞膜的磷脂双分子层是离子电流的不良导体，因为它不能渗透离子。 然而，膜却包含通道蛋白质，其允许离子穿过它。 膜中有两种类型的离子通道：门控和非门控。 非门控离子通道始终是打开的，而门控通道可以打开或关闭状态，打开的可能性通常取决于膜电位——称为电压型门控通道。门控通道通常只对特定类型的离子开放。膜对特定离子的渗透性取决于对该离子有选择性的开放通道的数量。大多数门控通道在静息状态下处于关闭状态。 因此，非离子通道主要负责建立静息电位。而当产生动作地位时，门控通道除以打开状态，允许离子通过细胞膜。

由于浓度差异，钠离子和氯离子倾向于扩散到细胞内，而钾离子倾向于向外扩散。 注意，由于细胞膜内外的正负电荷会产生电场，所以离子不会彻底的从细胞内扩散到细胞外，反之亦然。

例如，假设细胞只能透过K +。 K +的浓度梯度将K +离子移出细胞。 然而，K +的持续外流在电池外部积聚了过量的正电荷，并在内部留下了过量的负电荷。 负电荷主要由不可渗透的有机阴离子A-组成，这种电荷的积累阻碍了K +进一步流出，从而达到平衡。在这种平衡状态下，电和化学驱动力相等。K +离子在膜上平衡的膜电位称为钾离子的能斯特电位或平衡电位或反转电位。

钾离子的能斯特电位表达式如下所示：

这里，EK是钾离子的能斯特电位，R是气体常数，T是温度，z是钾离子的化合价，F是法拉第常数，[K +] out和[K +] in是K +离子在细胞内外的浓度。该公式也同样适用于其他的离子。

除了K +之外，静息状态下的神经元对Na +和Cl-也是可渗透的。由于它们的各自的细胞内外浓度差异，Na +和Cl-离子趋向于进入细胞而K +离子趋向于向细胞外移动。Na +离子的流入倾向于使细胞去极化，而K +的流出和Cl-的流入具有相反的效果。细胞的静息电位取决于细胞内外的离子浓度，以及细胞膜对每种离子的渗透性。 另外，在静息状态下，K +和Cl-通道开放的很多。因此，可以推出细胞的静息电位主要由K +和Cl-能斯特电位决定。

能斯特方程（Nernst Equation）

假设细胞膜只能渗透一种离子，那么该离子的能斯特势就是电和化学驱动力平衡的静息电位。在下文中，[C]（x）为某些离子的浓度，V（x）为跨越膜的点x处的电位。 根据菲克扩散定律可知，扩散通量J_diff为：

负责离子被动运动的另一个物理力是欧姆定律的微观形式所描述的电漂移：

电场E是电压V的梯度（以伏特为单位测量），因此具有伏特/厘米的单位。 z是离子的化合价（±1;±2等）。参数μ是迁移率，[C]为浓度。浓度越高，漂移越大。

穿过膜的总通量由这两者的总和为J_total：

爱因斯坦关系将迁移率与扩散系数联系起来：

其中k是玻尔兹曼常数，T是绝对温度，q是电荷（以库仑计）。因此，我们可以将总通量写为：

通过除以阿伏加德罗的数字，将该等式转换为单个分子的数量为其摩尔当量是方便的。用RT=F代替kT=q，其中R是理想气体常数，F是法拉第常数。 这将产生每摩尔的通量。 将此通量乘以化合价z的平方和法拉第常数F得到电流通量：

通过将电流设置为零来获得能斯特方程。也就是说，对于给定的离子种类，在平衡时，扩散和电效应平衡：

综上可以推出能斯特方程：

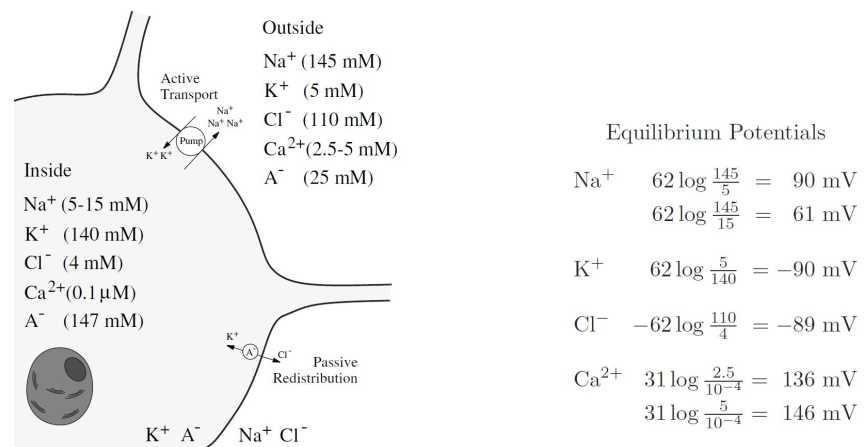
也就是说，当所有通量平衡时发生的平衡或能斯特电势取决于细胞内部和外部离子浓度比的对数。

典型哺乳动物神经元中的离子浓度和它们的能斯特平衡电位图

参考文献
[1]: Izhikevich, E. M. 2007 Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting. The MIT press.
[2]: https://baike.baidu.com/item/脑细胞/2760506?fr=aladdin
[3]: Wulfram Gerstner，Neuronal Dynamics – From Single Neurons to Networ.[M],Cambridge University Press.

今天的文章计算神经科学（二）分享到此就结束了，感谢您的阅读。