1.从两个角度理解

（1）信息论中交叉熵

$$H(p,q)=-\sum _{x}p(x)log(q(x))=H(p)+D_{KL}(p||q)$$
p是指真实的分布，q是估计的分布。式中$H(p)$是真实分布的熵，当给定分布，熵就确定；$D_{KL}(p||q)$是相对熵。
softmax分类器就是要最小化估计分类概率和真实分布之间的交叉熵。
交叉熵用于评估两个分布的相似度。

（2）概率的角度

softmax函数$P(y_i|x_i,w)=\frac{e^{f_{y_i}}}{{\sum }_j{e}^{f_j}}$
给定输入$x_i$和参数w，分配给正确分类标签的归一化概率。

2. softmax在实际应用中的问题

softmax函数中分子和分母都做指数运算，当数值很大的时候，会出现指数爆炸等问题。
常用的处理方法是分子分母同时乘以一个常数C，
$$\frac{e^{f_{y_i}}}{{\sum }_j{e}^{f_j}}=\frac{C{e}^{f_{y_i}}}{C{\sum }_j{e}^{f_j}}=\frac{e^{f_{y_i}+logC}}{{\sum }_j{e}^{f_j+logC}}$$
C通常取值为$-max(f_j)$,使最大的值为0.

# python实现
 f -= np.max(f)
 p = np.exp(f)/np.sum(np.exp(f))

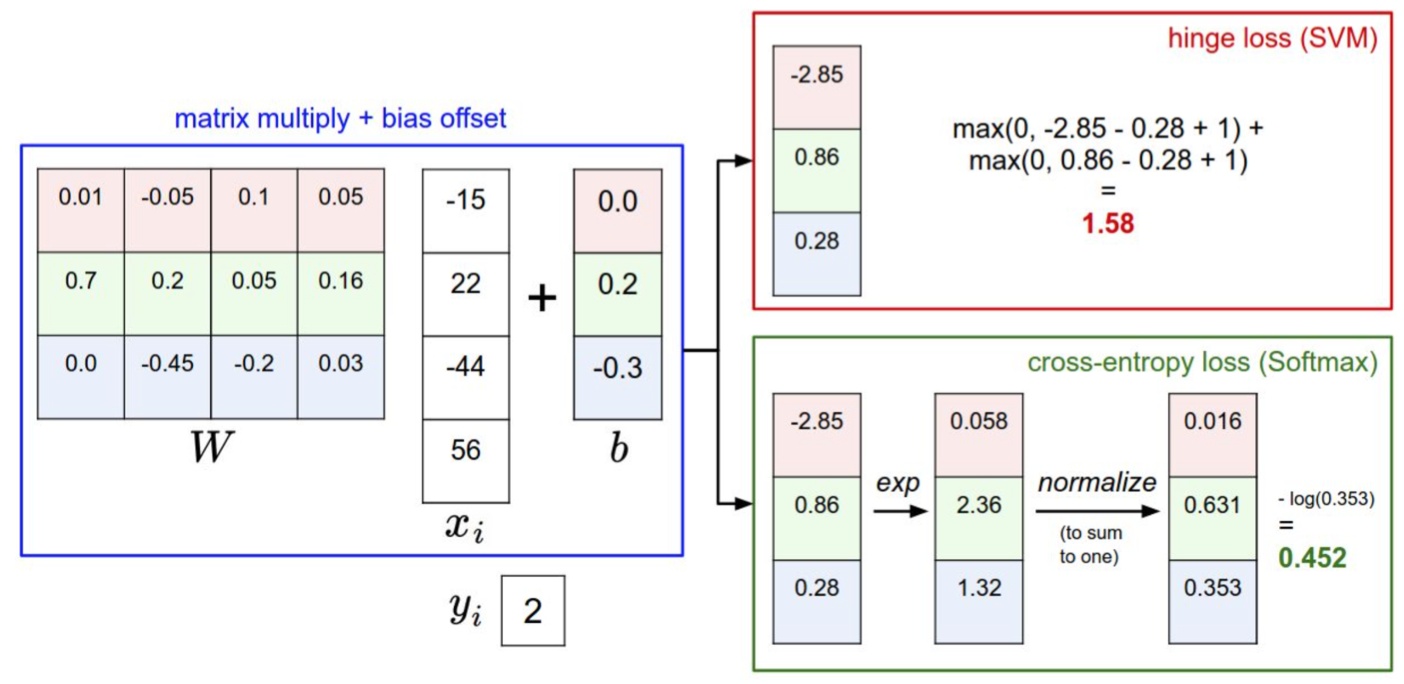
3. 一个简单的示例

这里需要强调的是：最后的输出直接由权重上一层的输出+偏置求得，并没有经过sigmoid函数，所以上图输出结果是$[-2.85,0.86,0.28]$。
(1) 先求$e^{f_j}$,
$$[e^{-0.285},e^{0.86},e^{0.28}]=[0.058,2.36,1.32]$$
(2) 求${\sum }_j{e}^{f_j}$
$$e^{-0.285}+e^{0.86}+e^{0.28}=0.058+2.36+1.32=3.738$$
(3) 求输出概率
$$P(y_1|x_1,w)=\frac{e^{f_{y_1}}}{{\sum }_j{e}^{f_j}}=\frac{0.058}{3.738}=0.016$$
$$P(y_2|x_1,w)=\frac{e^{f_{y_2}}}{{\sum }_j{e}^{f_j}}=\frac{2.36}{3.738}=0.631$$
$$P(y_3|x_1,w)=\frac{e^{f_{y_3}}}{{\sum }_j{e}^{f_j}}=\frac{1.32}{3.738}=0.0353$$

给一个类别的打分为$[1,-2,0]$,softmax通过上述的计算，得到概率输出$[0.7,0.04,0.26]$。
进一步考虑正则项的影响，假设惩罚使得得分的输出变为原来的$\frac{1}{2}$，即$[1,-2,0]$=>$[0.5,-1,0]$时，最终得到的输出为$[0.55,0.12,0.33]$。
softmax分类器会使正确的分类获得更大的概率，使错误的分类得到更小的概率。

（1）CS231n课程笔记翻译：线性分类笔记（下）
https://zhuanlan.zhihu.com/p/21102293?refer=intelligentunit
（2）cs231n-assignment1-SVM/Softmax/two-layer-nets梯度求解
https://blog.csdn.net/pjia_1008/article/details/66972060
（3）CS231n课程学习笔记（三）——Softmax分类器的实现
https://blog.csdn.net/stalbo/article/details/79379078
（4）斯坦福大学深度学习公开课cs231n学习笔记（9）softmax分类和神经网络分类代码实现
https://blog.csdn.net/piaoxuezhong/article/details/78818572

今天的文章softmax 分类器分享到此就结束了，感谢您的阅读。