分治法——合并排序（归并排序）

合并排序（归并排序）

合并排序是成功应用分治技术的一个完美例子。对于一个需要排序的数组A[0…n-1],合并排序把它一分为二：$A[0..\lfloor n/2\rfloor -1]和A[\lfloor n/2\rfloor ..n-1]$，并对每个子数组递归排序，然后把这两个排好序的子数组合并为一个有序数组。对两个有序数组的合并(merging)可以通过merge的算法完成。初始状态下，两个指针（数组下标)分别指向两个待合并数组的第一个元素。然后比较这两个元素的大小，将较小的元素添加到一个新创建的数组中。接着，被复制数组中的指针后移，指向该较小元素的后继元素。上述操作一直持续到两个数组中的一个被处理完为止。然后，在未处理完的数组中，剩下的元素被复制到新数组的尾部。
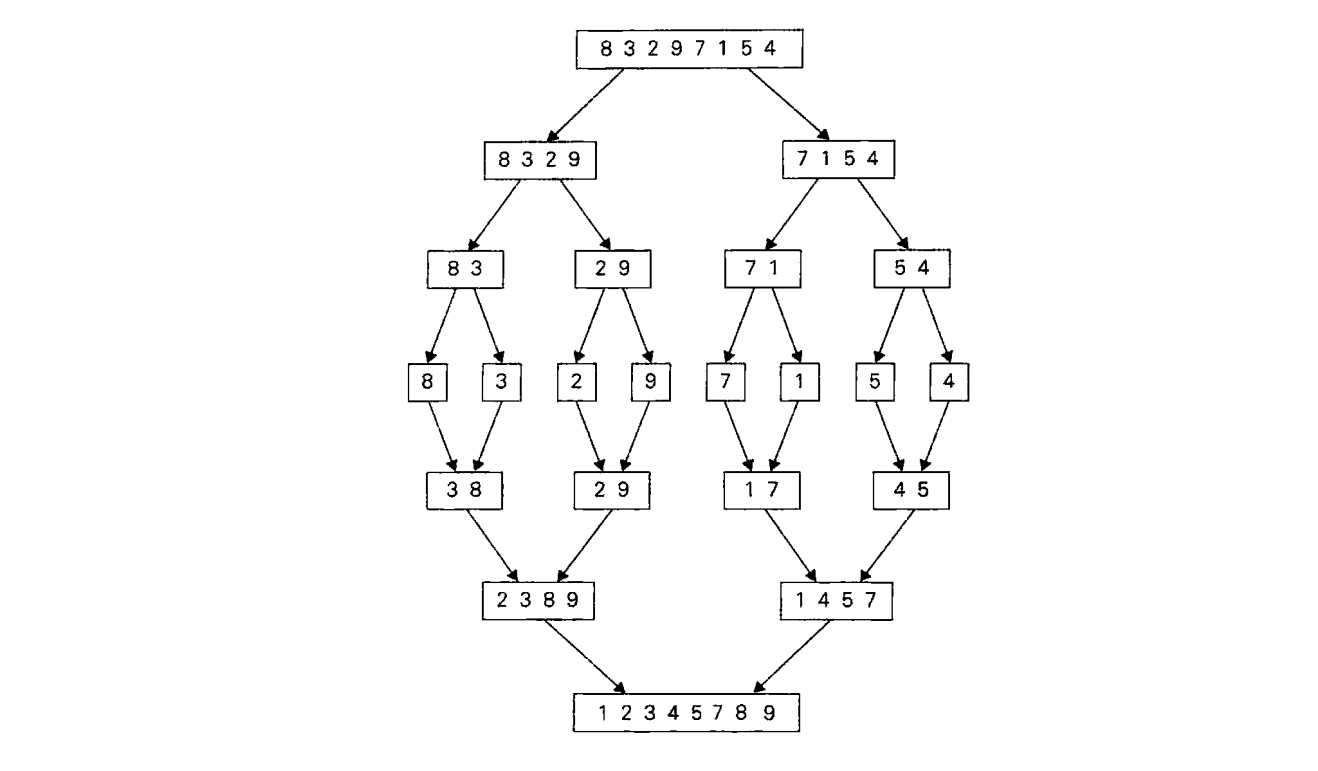
下图是对数列8，3，2，9，7，1，5，4进行排序的操作过程：

伪代码

MergeSort(A[0..n-1])
	//递归调用mergesort来对数组A[0..n-1]排序
	//输入：一个可排序数组A[0..n-1]
	//输出：非降序排列的数组A[0..n-1]
	if n > 1
		copy A[0..⌊n/2⌋−1] to B[0..⌊n/2⌋−1]
		copy A[⌊n/2⌋..n−1] to C[0..⌊n/2⌋−1]
		MergeSort(B[0..⌊n/2⌋−1])
		MergeSort(C[⌊n/2⌋..n−1])
		Merge(B,C,A)

Merge(B[0-.p-1],C[0..q-1],A[0..p+q-1]）
	//将两个有序数组合并为一个有序数组
	//输入：两个有序数组B[0..p-1]和C[0..q-1]
	//输出：A[0..p+q-1]中已经有序存放了B和C中的元素<-
	i <- 0;j <- 0;k <- 0
	while i < p and j < q do
		if B[i] <= C[j]
			A[k]<-B[i];i <- i+1
		else A[k] <- C[j]; j <- j+1
		k <- k + 1
	if i = p copy C[j..q-1] to A[A..p+q-1]
	else copy B[i..p-1] to A[A..p+q-1]

Java代码实现

package com.算法.分治法;

import java.util.Arrays;

/** * @Author Lanh **/
public class 合并排序 { 
   
    public static void main(String[] args) { 
   
        int[] arr = { 
   8,3,2,9,7,1,5,4};
        mergeSort(arr);
        System.out.println(Arrays.toString(arr));
    }

    public static void mergeSort(int[] arr){ 
   
        if (arr.length>1){ 
   
            int len = arr.length;
            int mid = len/2;
            int[] A = new int[mid];
            int[] B = new int[len-mid];
            System.arraycopy(arr,0,A,0,mid);
            System.arraycopy(arr,mid,B,0,len-mid);
            mergeSort(A);
            mergeSort(B);
            merge(A,B,arr);
        }
    }

    public static void merge(int[] A,int[] B ,int[] arr){ 
   
        int p = A.length;
        int q = B.length;
        int i = 0;
        int j = 0;
        int k = 0;
        while (i<p&&j<q){ 
   
            if (A[i]<B[j]) { 
   
                arr[k] = A[i];
                i++;
            }else { 
   
                arr[k] = B[j];
                j++;
            }
            k++;
        }
        if (i==p){ 
   
            System.arraycopy(B,j,arr,k,q-j);
        }else System.arraycopy(A,i,arr,k,p-i);
    }
}

今天的文章分治法——合并排序（归并排序）分享到此就结束了，感谢您的阅读。