控制工程基础学习笔记-第3章 时域瞬态响应分析

第3章 时域瞬态响应分析

3.1 时域响应及典型输入信号

稳态响应：系统在时间上趋于无穷大时的输出状态。
瞬态响应：输入信号作用下，输出量从初始状态到稳定状态的响应过程。
典型的输入信号有阶跃信号，斜坡信号，加速度信号，脉冲信号以及正弦信号，这些在第二章都已经提到过了，这里就不过多赘述了。
值得一提的是，由于单位脉冲函数拉式变换后它的象函数等于1，因此当系统输入为单位脉冲脉冲函数时，系统的脉冲响应函数等于系统的传递函数。
当系统输入任一时间函数时，我们可以利用脉冲函数这一良好的性质，把输入信号分割为n个脉冲。然后把输出函数通过这种方法再叠加起来就好了。
按比例和时间平移的方法，可得${\tau }_k$时刻的响应为$x({\tau }_k)g(t-{\tau }_k)\Delta \tau$
所以
$$\begin{array}{rl}y(t)& =\underset{n\to \infty }{\lim }\sum _{k=0}^{n}x({\tau }_k)g(t-{\tau }_k)\Delta \tau \\ & ={\int }_0^{t}x(\tau )g(t-\tau )\mathrm{d}\tau \end{array}$$
也就是说，输出响应为输入函数与脉冲函数的卷积，脉冲响应函数由此又得名权函数。这一结论其实也可以通过拉式变换的卷积定理来印证。

3.2 一阶系统的瞬态响应

能够用一阶微分方程描述的系统。它的典型形式是一阶惯性环节。
$$\frac{X_o(s)}{X_i(s)}=\frac{1}{Ts+1}$$

3.2.1 一阶系统的单位阶跃响应

单位阶跃输入为$x_i(t)=1(t)$。象函数为$X_i(s)=\frac{1}{s}$。则：
$$X_o(s)=\frac{1}{Ts+1}\cdot \frac{1}{s}=\frac{1}{s}-\frac{T}{Ts+1}=\frac{1}{s}-\frac{1}{s+\frac{1}{T}}$$
经过拉式反变换：
$$x_o(t)=\left(1-{\mathrm{e}}^{-\frac{1}{T}t}\right)1(t)$$
值得记住的特点只有一条，一阶系统的单位阶跃响应的调整时间为$(3-4)T$。

3.2.2 一阶系统的单位斜坡响应

单位斜坡输入为$x_i(t)=t\cdot 1(t)$。它的象函数为$X_i(s)=\frac{1}{s^2}$。由此得：
$$X_o(s)=\frac{1}{Ts+1}\cdot \frac{1}{s^2}=\frac{1}{s^2}-\frac{T}{s}+\frac{T}{s+\frac{1}{T}}$$
经过拉式反变换后：
$$x_o(t)=(t-T+T{\mathrm{e}}^{-\frac{1}{T}t})1(t)$$
对输入和输出做差可以得到误差函数$e(t)=x_i(t)-x_o(t)=T-T{\mathrm{e}}^{-t/T}$

3.2.3 一阶系统的单位脉冲响应

单位脉冲输入$x_i(t)=\delta (t)$。象函数为$X_i(s)=1$。
经过简单的计算可以的得到：
$$x_o(t)=\left(\frac{1}{T}{\mathrm{e}}^{-\frac{1}{T}t}\right)1(t)$$
一阶系统的瞬态响应小结

我们分析一下输入和输出的关系不难得出如下的结论。对于线性定常系统：输入微分（或积分）的输出等于原输出的微分（或积分）。
我们可以简单地说明一下理由。设一个系统的传递函数为$G(s)$，对于$x_i(t)$的响应为$x_o(t)$。也就是说$x_o(t)=L^{-1}[X_o(s)]=L^{-1}[G(s)X_i(s)]$。而如果输入为${\dot{x}}_i(t)$，则$输出=L^{-1}[G(s)s{X}_i(s)]=L^{-1}[sG(s)X_i(s)]=L^{-1}[s{X}_o(s)]={\dot{x}}_o(t)$。

3.3 二阶系统的瞬态响应

我们通常有两种形式来描述二阶系统：
形式一：
$$\frac{X_o(s)}{X_i(s)}=\frac{{\omega }_n^2}{s^2+2\zeta {\omega }_{n}s+{\omega }_n^2}$$
形式二：
$$\frac{X_o(s)}{X_i(s)}=\frac{1}{T^2{s}^2+2\zeta Ts+1}$$
其中$T=1/{\omega }_n$

3.3.1 二阶系统的单位阶跃响应

响应的象函数为：
$$X_o(s)=\frac{{\omega }_n^2}{s^2+2\zeta {\omega }_{n}s+{\omega }_n^2}\cdot \frac{1}{s}$$
下面我们要根据二阶系统的极点分布特点，分五种情况进行讨论。
下面开始顺便一起复习机械振动。如果想要按照机械振动的语境来研究这个问题，可以看我这一篇博客

3.3.1.1 欠阻尼$0<\zeta <1$

我们对传递函数进行变形：
$$\frac{X_o(s)}{X_i(s)}=\frac{{\omega }_n^2}{(s+\zeta {\omega }_n+\mathrm{j}{\omega }_d)(s+\zeta {\omega }_n-\mathrm{j}{\omega }_d)}$$
式中，${\omega }_d={\omega }_n\sqrt{1-{\zeta }^2}$，我们称${\omega }_d$为阻尼自振角频率。
把单位阶跃输入代入其中得到：（我这么和你说吧，这一波计算，我算了半个小时，所以建议下面的结论还是记住比较好）
$$X_o(s)=\frac{1}{s}-\frac{s+\zeta {\omega }_n}{(s+\zeta {\omega }_n{)}^2+{\omega }_d^2}-\frac{\zeta {\omega }_n}{(s+\zeta {\omega }_n{)}^2+{\omega }_d^2}$$
经过拉式反变换得到：
$$x_o(t)=\left(1-{\mathrm{e}}^{-\zeta {\omega }_{n}t}\mathrm{c}\mathrm{o}\mathrm{s}({\omega }_{d}t)-\frac{\zeta }{\sqrt{1-{\zeta }^2}}{\mathrm{e}}^{-\zeta {\omega }_{n}t}\mathrm{s}\mathrm{i}\mathrm{n}({\omega }_{d}t)\right)1(t)$$
不建议直接记忆拉式反变换的结论，可以记忆一下这个式子：
$$X_o(s)=\frac{1}{s}-\frac{s+2\zeta {\omega }_n}{(s+\zeta {\omega }_n{)}^2+{\omega }_d^2}$$
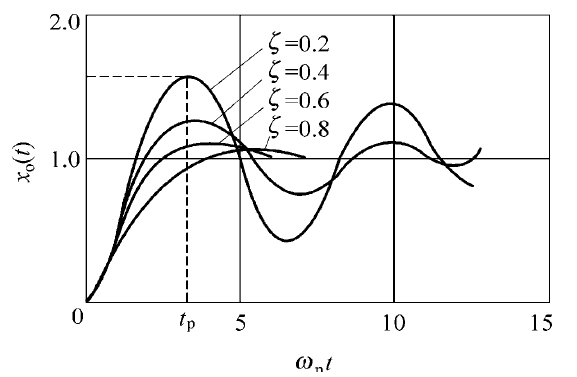
对于欠阻尼系统有如下特点：

1. 以${\omega }_d$为角频率衰减振荡；
2. 随着$\zeta$的减小，振荡幅度加大。
   画在一张图上如下所示：
   

3.3.1.2 临界阻尼$\zeta =1$

运用刚才我们需要记住的式子进行变形：
$$X_o(s)=\frac{1}{s}-\frac{s+2\zeta {\omega }_n}{(s+\zeta {\omega }_n{)}^2+{\omega }_d^2}$$
代入$\zeta =1$得到${\omega }_d=0$，进一步得到：
$$\begin{array}{rl}{X}_o(s)& =\frac{1}{s}-\frac{s+2{\omega }_n}{(s+{\omega }_n{)}^2}\\ & =\frac{1}{s}-\frac{s+{\omega }_n}{(s+{\omega }_n{)}^2}-\frac{{\omega }_n}{(s+{\omega }_n{)}^2}\\ & =\frac{1}{s}-\frac{1}{(s+{\omega }_n)}-\frac{{\omega }_n}{(s+{\omega }_n{)}^2}\end{array}$$
对之进行拉式反变换：
可以得到结论：
$$x_o(t)=(1-{\mathrm{e}}^{-{\omega }_{n}t}-{\omega }_{n}t{\mathrm{e}}^{-{\omega }_{n}t})1(t)$$

3.3.1.3 过阻尼$\zeta >1$

式子特别长，但是我觉得考试不会考这种情况，过阻尼好像大家一般都不太研究它。
记住它没有超调，过渡时间长就好了。超调是什么马上就来解释。

3.3.1.4 零阻尼$\zeta =0$

同样利用我们之前记住的式子：
$$X_o(s)=\frac{1}{s}-\frac{s+2\zeta {\omega }_n}{(s+\zeta {\omega }_n{)}^2+{\omega }_d^2}$$
代入$\zeta =0$，可得${\omega }_d={\omega }_n$，由此可得：
$$X_o(s)=\frac{1}{s}-\frac{s}{s^2+{\omega }_n^2}$$
经过拉式反变换可得：
$$x_o(t)=(1-\mathrm{c}\mathrm{o}\mathrm{s}({\omega }_{n}t))1(t)$$
零阻尼情况下，输入信号后维持等幅振荡。

3.3.1.4 负阻尼$\zeta <0$

系统是发散不稳定的，一般机械系统不会遇到这种情况。
可能存在两种情况：

3.3.2 二阶系统的单位脉冲响应

单位脉冲响应输入的原函数为$x_i(t)=\delta (t)$象函数为$X_i(s)=1$。由此可以得到$X_o(s)=\frac{{\omega }_n^2}{s^2+2\zeta {\omega }_{n}s+{\omega }_n^2}\cdot 1$。我们分三种情况来讨论这个问题。

3.3.2.1 欠阻尼$0<\zeta <1$

我们将原来的式子进行变形可以得到：
$$X_o(s)=\frac{{\omega }_n^2}{(s+\zeta {\omega }_n+\mathrm{j}{\omega }_d)(s+\zeta {\omega }_n-\mathrm{j}{\omega }_d)}=\frac{\frac{{\omega }_n}{\sqrt{1-{\zeta }^2}}{\omega }_d}{(s+\zeta {\omega }_n{)}^2+{\omega }_d^2}$$
上面这步变形并没有用到第二章提到的那些方法，就是简单的把分母配成完全平方，把分子的${\omega }_n^2$变形成一个${\omega }_n$乘以一个${\omega }_d$和一个系数的形式。这样一来我们就可以简单地进行一个拉氏变换，得到：
$$x_o(t)=\left(\frac{{\omega }_n}{\sqrt{1-{\zeta }^2}}{\mathrm{e}}^{-\zeta {\omega }_{n}t}\mathrm{s}\mathrm{i}\mathrm{n}({\omega }_{d}t)\right)1(t)$$
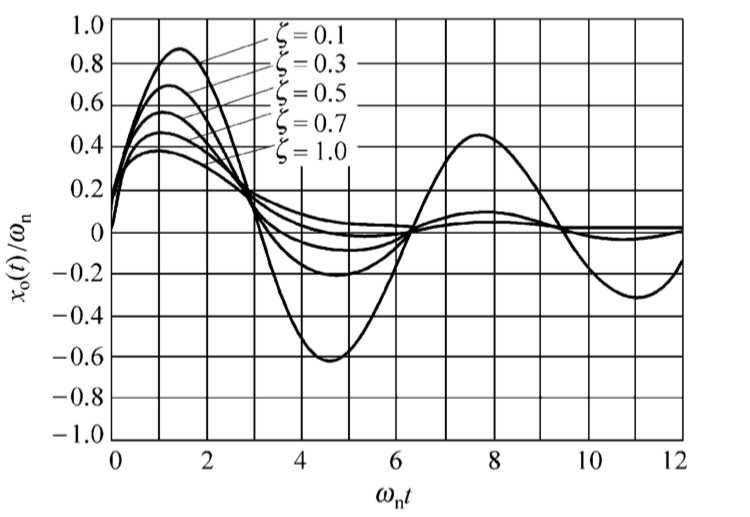
响应的图像和阶跃响应类似，但是有所不同：

特点和阶跃响应类似。

3.3.2.2 临界阻尼$\zeta =1$

响应的象函数为：
$$X_o(s)=\frac{{\omega }_n^2}{(s+{\omega }_n{)}^2}$$
那么利用衰减定理和斜坡函数的拉氏变换我们可以得到这个象函数的原函数为：
$$x_o(t)=({\omega }_n^{2}t{\mathrm{e}}^{-{\omega }_{n}t})1(t)$$

3.3.2.3 过阻尼$\zeta >1$

式子特别长，打了也记不住。下面把三种情况下的响应图像汇总到一张图上看一下：

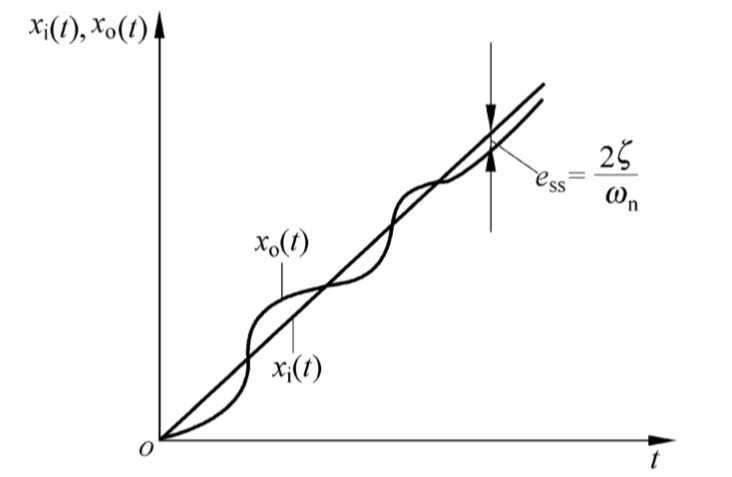
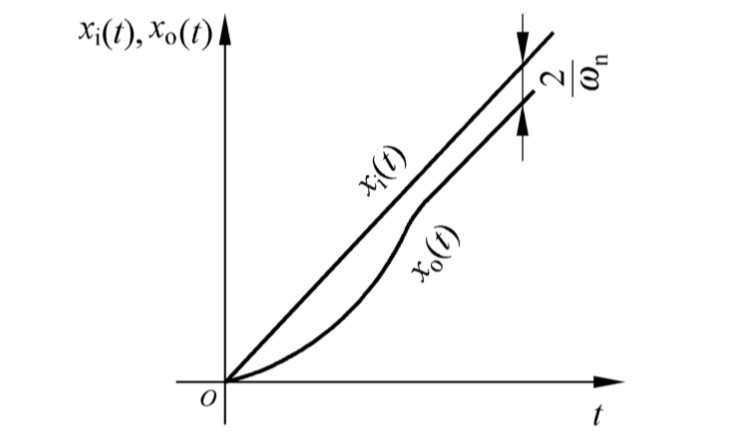
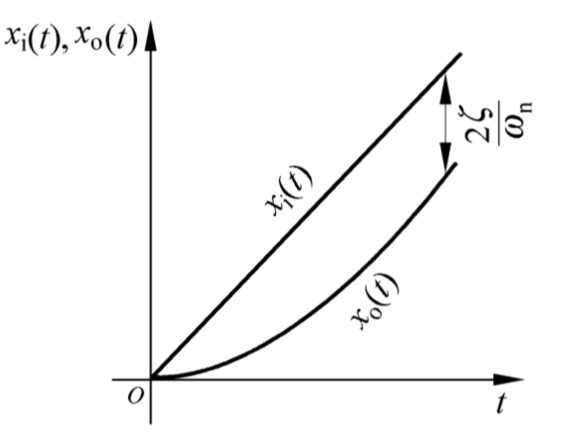
3.3.3 二阶系统的单位斜坡响应

单位斜坡函数的象函数为$\frac{1}{s^2}$。这个系统的响应为：
$$X_o(s)=\frac{{\omega }_n^2}{s^2+2\zeta {\omega }_{n}s+{\omega }_n^2}\cdot \frac{1}{s^2}$$
这里上课的时候老师好像也没有讨论它响应的数学表达式。想想也是，一对重极点，一对共轭极点，zu kompliziert。
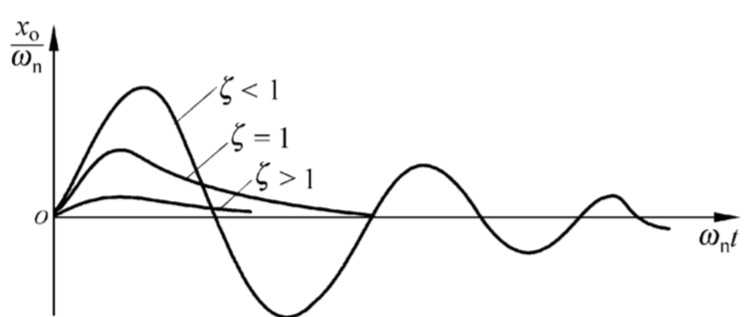
我们就看看图吧：
欠阻尼：

临界阻尼：

过阻尼：

3.3这一部分基本上和机械振动的内容的重合度非常高可以对比着开展学习。

3.4 时域分析性能指标

据说老师考研面试的时候问过控制系统性能的三大特性，值得注意一下。