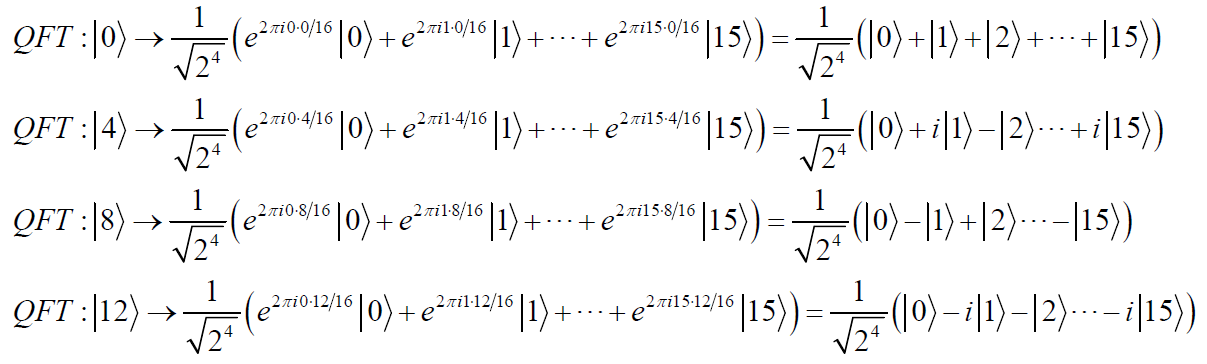《基于张量网络的机器学习入门》学习笔记8
Shor算法
来源
1994 1994 1994年,应用数学家 S h o r Shor Shor提出了 一个实用的量子算法,通常称为 S h o r Shor Shor算法。其思想是将整数质因子分解问题转化为求解量子傅里叶变换的周期, 将多个输入制备为量子态叠加, 进行并行处理和操作, 从而达到了量子加速的目的,可以在多项式时间内完成大整数质因数分解。所以 S h o r Shor Shor算法从诞生之时,就和以 R S A RSA RSA算法为根基的加密技术形成了不可调和的矛盾。
Shor算法的大致流程
完整的 S h o r Shor Shor算法需要经典计算机和量子计算机协作完成。其中量子计算机实现一个周期查找的函数,经典计算机负责整个算法流程的控制,以及调用量子算法。我们可以简单的讲 S h o r Shor Shor算法分成两个部分:
1.第一部分是讲因子分解问题转化为成周期问题,这部分可以用传统方式实现。
2.第二部分则是使用量子手段来搜寻这个周期,这一部分是 S h o r Shor Shor算法中体现量子加速的主要部分!
因数分解
假设待分解的整数为 N N N,分解步骤为:
1.选择任意数字 1 < a < N 1<a<N 1<a<N;
2.计算 g c d ( a , N ) gcd(a,N) gcd(a,N),要满足 g c d ( a , N ) = 1 gcd(a,N)=1 gcd(a,N)=1,即 a a a与 N N N互质,否则返回第一步;
3.构造函数 f ( x ) = a x m o d N f(x)=a^xmodN f(x)=axmodN,并且寻找最小周期 r r r,使得 f ( x + r ) = f ( x ) f(x+r)=f(x) f(x+r)=f(x);(此为量子计算步骤)
4.若 r r r为奇数,则返回第一步;
5.若 a r 2 m o d N = − 1 a^{\frac{r}{2}}modN=-1 a2rmodN=−1,返回第一步;若 a r 2 m o d N ≠ − 1 a^{\frac{r}{2}}modN\ne-1 a2rmodN=−1,则 g c d ( a r 2 ± 1 , N ) gcd(a^{\frac{r}{2}}\pm1,N) gcd(a2r±1,N)所求的质因数为 p = g c d ( g c d ( a r 2 + 1 , N ) , q = g c d ( g c d ( a r 2 − 1 , N ) p=gcd(gcd(a^{\frac{r}{2}}+1,N),q=gcd(gcd(a^{\frac{r}{2}}-1,N) p=gcd(gcd(a2r+1,N),q=gcd(gcd(a2r−1,N),至此,完成分解。
下面我们看一个具体的例子:
例用 S h o r Shor Shor算法对 N = 15 N=15 N=15进行分解。
不妨取 a = 7 a=7 a=7,其满足 g c d ( 7 , 15 ) = 1 gcd(7,15)=1 gcd(7,15)=1,因此,构造函数为 f ( x ) = 7 x m o d 15 f(x)=7^xmod15 f(x)=7xmod15,有:
f ( 0 ) = 7 0 m o d 15 = 1 , f ( 1 ) = 7 1 m o d 15 = 7 , f ( 2 ) = 7 2 m o d 15 = 4 , f ( 3 ) = 7 3 m o d 15 = 13 , f ( 4 ) = 7 4 m o d 15 = 1 , f ( 5 ) = 7 5 m o d 15 = 7 , f ( 6 ) = 7 6 m o d 15 = 4 , f ( 7 ) = 7 7 m o d 15 = 13 , f ( 85 ) = 7 8 m o d 15 = 1 , f ( 9 ) = 7 9 m o d 15 = 7 , f ( 10 ) = 7 10 m o d 15 = 4 , f ( 11 ) = 7 11 m o d 15 = 13. f(0)=7^0mod15=1,f(1)=7^1mod15=7,f(2)=7^2mod15=4,f(3)=7^3mod15=13,\\ f(4)=7^4mod15=1,f(5)=7^5mod15=7,f(6)=7^6mod15=4,f(7)=7^7mod15=13,\\ f(85)=7^8mod15=1,f(9)=7^9mod15=7,f(10)=7^{10}mod15=4,f(11)=7^{11}mod15=13. f(0)=70mod15=1,f(1)=71mod15=7,f(2)=72mod15=4,f(3)=73mod15=13,f(4)=74mod15=1,f(5)=75mod15=7,f(6)=76mod15=4,f(7)=77mod15=13,f(85)=78mod15=1,f(9)=79mod15=7,f(10)=710mod15=4,f(11)=711mod15=13.
不难看出,周期 r = 4 r=4 r=4,且 a r 2 m o d N = 7 4 2 m o d 15 = 4 ≠ − 1 a^{\frac{r}{2}}modN=7^{\frac{4}{2}}mod15=4\ne-1 a2rmodN=724mod15=4=−1,那么有
p = g c d ( 50 , 15 ) = 5 , q = g c d ( 48 , 15 ) = 3 p=gcd(50,15)=5,q=gcd(48,15)=3 p=gcd(50,15)=5,q=gcd(48,15)=3
传统计算机储存的是数据,而量子计算机储存的是分解后的结果,这一步不需要任何计算成本。量子计算机再分解的时候其实就是储存的过程,每个正交状态对应一个素数,存储的过程天然就分解了这个数。尽量不要把 1 , 0 1,0 1,0的传统概念套上去,并不利于理解。比如 15 15 15怎么在量子态下表示?首先找到对应的正交态,则自然是素数了, 15 = 3 × 5 15=3\times5 15=3×5,那么, ∣ 15 ⟩ = ∣ 3 ⟩ + ∣ 5 ⟩ |15\rangle=|3\rangle+|5\rangle ∣15⟩=∣3⟩+∣5⟩就可以了,这里的正交态对应的就是传统的 1 , 0 1,0 1,0。
周期求取与量子傅里叶变换(QFT)
对两组有 m m m个量子比特的存储器进行幺正变换得到纠缠状态:
∑ i = 0 2 m − 1 ∣ x i ⟩ ⊗ ∣ f ( x i ) ⟩ , f ( x ) = a x m o d N \sum\limits_{i=0}^{2^m-1}|x_i\rangle\otimes|f(x_i)\rangle,f(x)=a^xmodN i=0∑2m−1∣xi⟩⊗∣f(xi)⟩,f(x)=axmodN
对量子位进行傅里叶变换,即:
Q F T : ∣ x ⟩ → 1 2 m ∑ k = 0 2 m − 1 e 2 π k x / 2 m ∣ k ⟩ QFT:|x\rangle\to\frac{1}{\sqrt{2^m}}\sum\limits_{k=0}^{2^m-1}e^{2\pi kx/2^m}|k\rangle QFT:∣x⟩→2m1k=0∑2m−1e2πkx/2m∣k⟩
可以看出,量子傅里叶变换就是将态前面的叠加系数变为原叠加系数的离散傅里叶变换。
将两个寄存器 R 1 R_1 R1和 R 2 R_2 R2初始化为 0 0 0,即:
∣ Ψ 0 ⟩ = ∣ R 1 ⟩ ∣ R 2 ⟩ = ∣ 0 ⟩ ∣ 0 ⟩ = ∣ 00 … ⟩ ∣ 00 … ⟩ |\Psi_0\rangle=|R_1\rangle|R_2\rangle=|0\rangle|0\rangle=|00\dots\rangle|00\dots\rangle ∣Ψ0⟩=∣R1⟩∣R2⟩=∣0⟩∣0⟩=∣00…⟩∣00…⟩
其中, R 1 R_1 R1存放函数的输入变量, R 2 R_2 R2存放计算结果。接着,对 R 1 R_1 R1中的每一位作 H H H变换,有:
H : ∣ Ψ 0 ⟩ → ∣ Ψ 1 ⟩ = 1 2 m ∑ x = 0 2 m − 1 ∣ x ⟩ ∣ 0 ⊗ f ( x ) ⟩ = 1 2 m ∑ x = 0 2 m − 1 ∣ x ⟩ ∣ a x m o d N ⟩ H:|\Psi_0\rangle\to|\Psi_1\rangle=\frac{1}{\sqrt{2^m}}\sum\limits_{x=0}^{2^m-1}|x\rangle|0\otimes f(x)\rangle=\frac{1}{\sqrt{2^m}}\sum\limits_{x=0}^{2^m-1}|x\rangle|a^xmodN\rangle H:∣Ψ0⟩→∣Ψ1⟩=2m1x=0∑2m−1∣x⟩∣0⊗f(x)⟩=2m1x=0∑2m−1∣x⟩∣axmodN⟩
此时, R 1 R_1 R1和 R 2 R_2 R2处于纠缠状态。
测量 ∣ R 2 ⟩ |R_2\rangle ∣R2⟩,并假设其态坍缩为 z = a l m o d N z=a^lmodN z=almodN。因为 f ( x ) f(x) f(x)的周期为 r r r,所以 a l m o d N = a l + j r m o d N ( l < r , j = 0 , 1 , ⋯ , A ) , A a^lmodN=a^{l+jr}modN(l<r,j=0,1,\cdots,A),A almodN=al+jrmodN(l<r,j=0,1,⋯,A),A是小于 ( 2 m − l ) / r (2^m-l)/r (2m−l)/r的最大整数,因此有:
x = l , l + r , ⋯ , l + A r x=l,l+r,\cdots,l+Ar x=l,l+r,⋯,l+Ar
∣ R 2 ⟩ |R_2\rangle ∣R2⟩坍缩时, ∣ R 1 ⟩ |R_1\rangle ∣R1⟩相对应地坍缩为:
∣ R 1 ⟩ = 1 A + 1 ∑ j = 0 A ∣ l + j r ⟩ |R_1\rangle=\frac{1}{\sqrt{A+1}}\sum\limits_{j=0}^A|l+jr\rangle ∣R1⟩=A+11j=0∑A∣l+jr⟩
可见, ∣ R 1 ⟩ |R_1\rangle ∣R1⟩是以 r r r为周期的一组态的叠加。若 2 m 2^m 2m是 r r r的整数倍,设 A = 2 m / r − 1 A=2^m/r-1 A=2m/r−1,有:
∣ R 1 ⟩ = r 2 m ∑ j = 0 2 m / r − 1 ∣ l + j r ⟩ = ∑ x = 0 2 m / r − 1 f ( x ) ∣ x ⟩ |R_1\rangle=\sqrt{\frac{r}{2^m}}\sum\limits_{j=0}^{2^m/r-1}|l+jr\rangle=\sum\limits_{x=0}^{2^m/r-1}f(x)|x\rangle ∣R1⟩=2mrj=0∑2m/r−1∣l+jr⟩=x=0∑2m/r−1f(x)∣x⟩
其中,若 x − l x-l x−l为 r r r的整数倍,那么 f ( x ) = r / 2 m f(x)=\sqrt{r/2^m} f(x)=r/2m;否则, f ( x ) = 0 f(x)=0 f(x)=0.
此时,对 ∣ R 1 ⟩ |R_1\rangle ∣R1⟩作量子傅里叶变换,有:
∣ R 1 ⟩ Q F T = ∑ c ∼ f ( c ) ∣ c ⟩ , f ~ ( c ) = r 2 m ∑ j = 0 2 m / r − 1 e 2 π ( l + j r ) c / 2 m = r 2 m e 2 π j r c / 2 m c |R_1\rangle_{QFT}=\sum_c\nolimits^{\sim}f(c)|c\rangle,\tilde{f}(c)=\frac{\sqrt{r}}{2^m}\sum\limits_{j=0}^{2^m/r-1}e^{2\pi(l+jr)c/2^m}=\frac{\sqrt{r}}{2^m}e^{2\pi jrc/2^m}c ∣R1⟩QFT=∑c∼f(c)∣c⟩,f~(c)=2mrj=0∑2m/r−1e2π(l+jr)c/2m=2mre2πjrc/2mc
当 c c c为 2 m / r 2^m/r 2m/r的整数倍时, r 2 m ∑ j = 0 2 m / r − 1 e 2 π ( l + j r ) c / 2 m = 2 m r \frac{\sqrt{r}}{2^m}\sum\limits_{j=0}^{2^m/r-1}e^{2\pi(l+jr)c/2^m}=\frac{2^m}{r} 2mrj=0∑2m/r−1e2π(l+jr)c/2m=r2m,否则 r 2 m ∑ j = 0 2 m / r − 1 e 2 π ( l + j r ) c / 2 m = 0 \frac{\sqrt{r}}{2^m}\sum\limits_{j=0}^{2^m/r-1}e^{2\pi(l+jr)c/2^m}=0 2mrj=0∑2m/r−1e2π(l+jr)c/2m=0
量子傅里叶变换增强了所需要的结果,使不需要的结果的概率为 0 0 0。由此可得,若 c c c为 2 m / r 2^m/r 2m/r的整数倍 k k k时,有:
∣ R 1 ⟩ Q F T = 1 r ∑ k = 0 r − 1 e 2 π l k ∣ k 2 m r ⟩ |R_1\rangle_{QFT}=\frac{1}{\sqrt{r}}\sum\limits_{k=0}^{r-1}e^{2\pi lk}|\frac{k2^m}{r}\rangle ∣R1⟩QFT=r1k=0∑r−1e2πlk∣rk2m⟩
即周期从 r r r变为 2 m / r 2^m/r 2m/r
此时测量 ∣ R 1 ⟩ |R_1\rangle ∣R1⟩_{QFT},得到 c ′ = k 2 m r c^{‘}=\frac{k2^m}{r} c′=rk2m,故 c ′ 2 m = k r \frac{c^{‘}}{2^m}=\frac{k}{r} 2mc′=rk。因为 c ′ c^{‘} c′和 2 m 2^m 2m均已知,若 g c d ( k , r ) = 1 gcd(k,r)=1 gcd(k,r)=1,则可求出 r r r。最大的 r r r记为所求的 f ( x ) f(x) f(x)的周期。
将 S h o r Shor Shor算法用于例 1 1 1可得:
∣ Ψ 3 ⟩ = 1 2 4 ∑ x = 0 2 4 − 1 ∣ x ⟩ ∣ a x m o d N ⟩ = 1 2 4 ( ∣ 0 , 1 ⟩ + ∣ 1 , 7 ⟩ + ∣ 2 , 4 ⟩ + ∣ 3 , 13 ⟩ + ∣ 4 , 1 ⟩ + ⋯ + ∣ 15 , 13 ⟩ ) = 1 2 4 [ ( ∣ 0 ⟩ + ∣ 4 ⟩ + ∣ 8 ⟩ + ∣ 12 ⟩ ) ⊗ ∣ 1 ⟩ + ⋯ ] |\Psi_3\rangle=\frac{1}{\sqrt{2^4}}\sum\limits_{x=0}^{2^4-1}|x\rangle|a^xmodN\rangle=\frac{1}{\sqrt{2^4}}(|0,1\rangle+|1,7\rangle+|2,4\rangle+|3,13\rangle+|4,1\rangle+\cdots+|15,13\rangle)\\ =\frac{1}{\sqrt{2^4}}[(|0\rangle+|4\rangle+|8\rangle+|12\rangle)\otimes|1\rangle+\cdots] ∣Ψ3⟩=241x=0∑24−1∣x⟩∣axmodN⟩=241(∣0,1⟩+∣1,7⟩+∣2,4⟩+∣3,13⟩+∣4,1⟩+⋯+∣15,13⟩)=241[(∣0⟩+∣4⟩+∣8⟩+∣12⟩)⊗∣1⟩+⋯]
投影算符 P ∣ 1 ⟩ = ∣ 1 ⟩ ⟨ 1 ∣ P_{|1\rangle}=|1\rangle\langle1| P∣1⟩=∣1⟩⟨1∣,有:
∣ Ψ 4 ⟩ = 1 2 4 = 1 2 4 ( ∣ 0 ⟩ + ∣ 4 ⟩ + ∣ 8 ⟩ + ∣ 12 ⟩ ) ⊗ ( ∣ 1 ⟩ ⟨ 1 ∣ ) ∣ 1 ⟩ |\Psi_4\rangle=\frac{1}{\sqrt{2^4}}=\frac{1}{2^4}(|0\rangle+|4\rangle+|8\rangle+|12\rangle)\otimes(|1\rangle\langle1|)|1\rangle ∣Ψ4⟩=241=241(∣0⟩+∣4⟩+∣8⟩+∣12⟩)⊗(∣1⟩⟨1∣)∣1⟩
已知,对 ∣ x ⟩ |x\rangle ∣x⟩作傅里叶变换为:
Q F T : ∣ x ⟩ → 1 2 m ∑ k = 0 2 m − 1 e 2 π i k x / 2 m ∣ k ⟩ = 1 2 4 ∑ k = 0 2 4 − 1 e 2 π i k x / 16 ∣ k ⟩ QFT:|x\rangle\to\frac{1}{\sqrt2^m}\sum\limits_{k=0}^{2^m-1}e^{2\pi ikx/2^m}|k\rangle=\frac{1}{\sqrt{2^4}}\sum\limits_{k=0}^{2^4-1}e^{2\pi ikx/16}|k\rangle QFT:∣x⟩→2m1k=0∑2m−1e2πikx/2m∣k⟩=241k=0∑24−1e2πikx/16∣k⟩
那么对 ∣ 0 ⟩ , ∣ 4 ⟩ , ∣ 8 ⟩ , ∣ 12 ⟩ |0\rangle,|4\rangle,|8\rangle,|12\rangle ∣0⟩,∣4⟩,∣8⟩,∣12⟩分别做傅里叶变换,有:
将上述四个式子相加可得:
1 4 ( ∣ 0 ⟩ + ∣ 4 ⟩ + ∣ 8 ⟩ + ∣ 12 ⟩ ) \frac{1}{\sqrt{4}}(|0\rangle+|4\rangle+|8\rangle+|12\rangle) 41(∣0⟩+∣4⟩+∣8⟩+∣12⟩)
由此,可以得到周期为 r = 4 r=4 r=4,且 a r 2 m o d N = 7 4 2 m o d 15 = 4 ≠ 1 a^{\frac{r}{2}}modN=7^{\frac{4}{2}}mod15=4\ne1 a2rmodN=724mod15=4=1,那么有 p = g d c ( 50 , 15 ) = 5 , q = g c d ( 48 , 15 ) = 3 p=gdc(50,15)=5,q=gcd(48,15)=3 p=gdc(50,15)=5,q=gcd(48,15)=3。
S h o r Shor Shor算法不能保证每次运行都能得到正确的结果。假设成功的概率是 1 − j 1-j 1−j,通过重复 k k k次实验,至少成功一次的概率为 1 − j k 1-j^k 1−jk。不难看出,可以通过增加实验的次数来提高实验成功的概率。所以 S h o r Shor Shor算法是一种随机算法。
今天的文章《基于张量网络的机器学习入门》学习笔记8(Shor算法)分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/6370.html