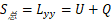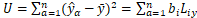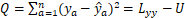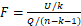非线性函数模型（多项式拟合）预测土壤侵蚀模数

某地区各地理单元的土壤侵蚀模数（x）与土壤含氮量1（y）的数据见（实验1数据中的“题目3”sheet）。

1. 画出二者之间的散点图并确定是什么样的相关形式；
2. 试用一个非线性函数模型拟合该地区土壤侵蚀模数（x）与土壤含氮量（y）的关系；
3. 检验该模型的显著性，并预测当土壤侵蚀模数x=8000t/(km2*a)时的土壤含氮量y。

1.	# coding=utf-8  
2.	import matplotlib.pyplot as plt  
3.	from matplotlib.font_manager import FontProperties  
4.	import numpy as np  
5.	from scipy.optimize import leastsq  
6.	plt.rcParams['font.sans-serif']=['SimHei'] #显示中文标签  
7.	plt.rcParams['axes.unicode_minus']=False   #这两行需要手动设置  
8.	myfont = FontProperties(fname="C:\Windows\Fonts\msyh.ttc")  
9.	Soil = [0.8, 1.4, 2, 2.7, 3.3, 4.1, 5.6, 6.5, 7.1, 7.7, 8.3, 9.2]  
10.	nitrogen = [6.6, 5.2, 4.8, 3.9, 3.7, 3.2, 2.4, 2.3, 2.1, 2.3, 1.7,1.5]  
11.	plt.figure(figsize=(12, 12), dpi=100)  
12.	plt.xticks(range(0, 10, 1))  
13.	plt.yticks(range(0, 10, 1))  
14.	plt.scatter(Soil, nitrogen,c='r')  
15.	plt.xlabel(u"土壤侵蚀模数x/103t.km-2.a-1",fontsize=24)  
16.	plt.ylabel(u"土壤含氮量y/g.m-2", fontsize=24)  
17.	plt.title(u"土壤侵蚀模数（x）与土壤含氮量（y）散点图", fontsize=36)  
18.	#plt.legend(loc='best')  
19.	plt.show() 

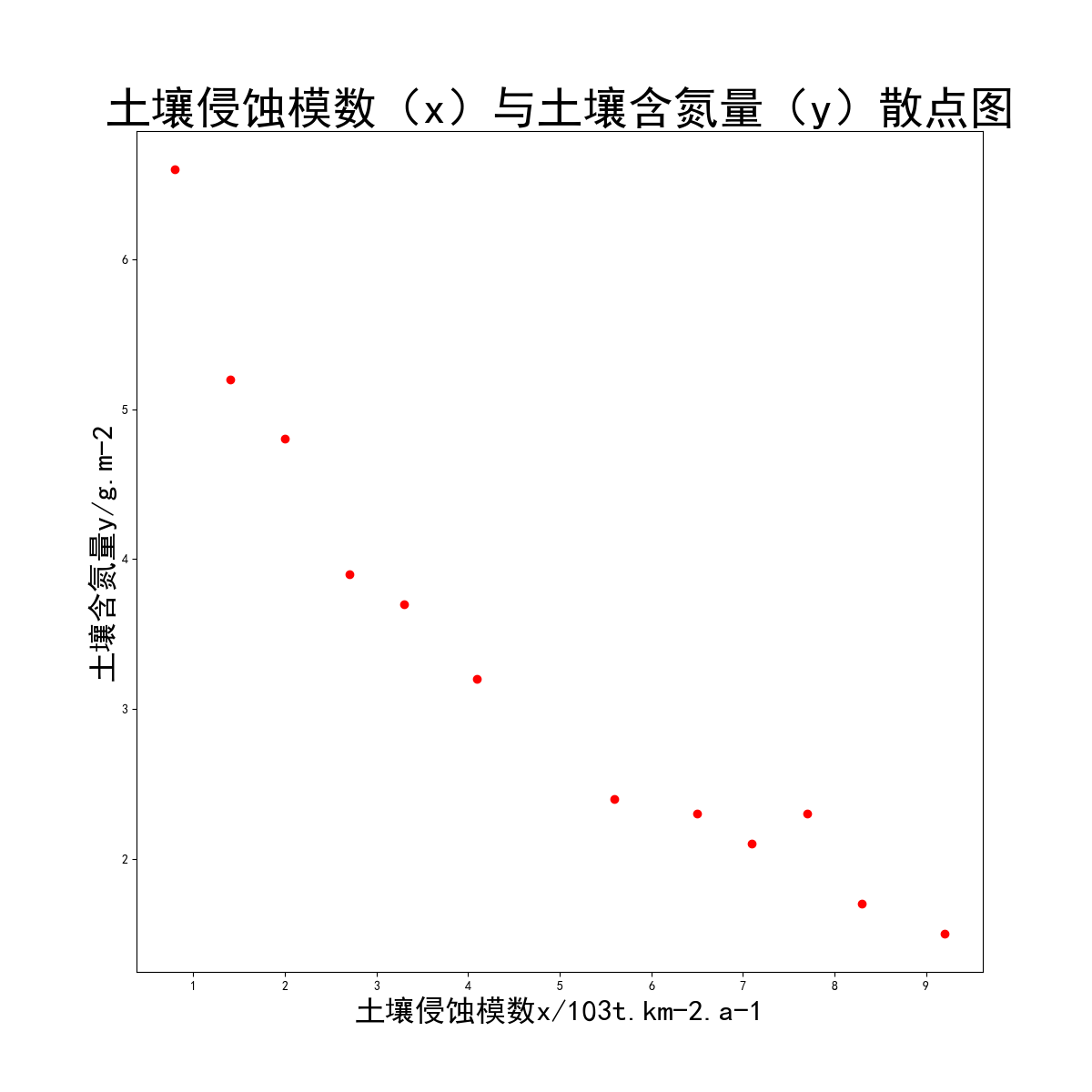
       由散点图可以看出，随着土壤侵蚀模数的增大，土壤含氮量减少，因此土壤侵蚀模数与土壤含氮量呈负相关关系。

多项式拟合

1.	import matplotlib.pyplot as plt  
2.	from matplotlib.font_manager import FontProperties  
3.	import numpy as np  
4.	from scipy.optimize import leastsq  
5.	plt.rcParams['font.sans-serif']=['SimHei'] #显示中文标签  
6.	plt.rcParams['axes.unicode_minus']=False   #这两行需要手动设置  
7.	myfont = FontProperties(fname="C:\Windows\Fonts\msyh.ttc")  
8.	  
9.	x = np.array([0.8, 1.4, 2, 2.7, 3.3, 4.1, 5.6, 6.5, 7.1, 7.7, 8.3, 9.2],dtype='float')  
10.	y = np.array([6.6, 5.2, 4.8, 3.9, 3.7, 3.2, 2.4, 2.3, 2.1, 2.3, 1.7,1.5], dtype='float')  
11.	  
12.	z1 = np.polyfit(x, y, 4) # 用4次多项式拟合，可改变多项式阶数；  
13.	p1 = np.poly1d(z1) #得到多项式系数，按照阶数从高到低排列  
14.	z2 = np.polyfit(x, y, 3) # 用3次多项式拟合，可改变多项式阶数；  
15.	p2 = np.poly1d(z2) #得到多项式系数，按照阶数从高到低排列  
16.	z3 = np.polyfit(x, y, 2) # 用2次多项式拟合，可改变多项式阶数；  
17.	p3 = np.poly1d(z3) #得到多项式系数，按照阶数从高到低排列  
18.	print(p1)  #显示多项式  
19.	print(p2)  #显示多项式  
20.	print(p3)  #显示多项式  
21.	yvals1=p1(x)  
22.	yvals2=p2(x)  
23.	yvals3=p3(x)  
24.	plt.plot(x, y, '*',label='original values')  
25.	plt.plot(x, yvals1, 'r',label='Quartic polynomial values')  
26.	plt.plot(x, yvals2, 'b',label='Cubic polynomial values')  
27.	plt.plot(x, yvals3, 'g',label='Quadratic polynomial')  
28.	plt.xlabel(u"土壤侵蚀模数x/103t.km-2.a-1",fontsize=12)  
29.	plt.ylabel(u"土壤含氮量y/g.m-2", fontsize=12)  
30.	plt.title(u"土壤侵蚀模数（x）与土壤含氮量（y）拟合图", fontsize=20)  
31.	plt.legend(loc=1) # 指定legend在图中的位置，类似象限的位置  
32.	plt.show()  
33.	  
34.	#利用相关系数矩阵计算R方  
35.	correlation1 = np.corrcoef(y, yvals1)[0,1]  
36.	correlation2 = np.corrcoef(y, yvals2)[0,1]  
37.	correlation3 = np.corrcoef(y, yvals3)[0,1]  
38.	  
39.	print(correlation1**2)  
40.	print(correlation2**2)  
41.	print(correlation3**2)  

四次拟合多项式为：y=0.00104×4 – 0.03558×3 + 0.4291×2- 2.472x +8.186 (R2= 0.9896)

三次拟合多项式为：y= -0.01473 x3 + 0.2913 x2 – 2.138 x + 7.957(R2=0.9892)

二次拟合多项式为：y=0.0707 x2 – 1.215 x + 7.02(R2=0.9695)

由此可以看出四次多项式R2最大，达0.9896，拟合效果最好，因此取拟合方程：y=0.00104×4 – 0.03558×3 + 0.4291×2- 2.472x +8.186

 F显著性检验：根据多元统计理论，若取Xi=xi，则实际模型的一元多项式非线性回归问题简化为多元线性回归问题，可根据多元线性回归方程的显著性检验多项式回归方程的显著性。y=0.00104×4 – 0.03558×3 + 0.4291×2- 2.472x +8.186转化为y=0.00104×4 – 0.03558×3 + 0.4291×2- 2.472×1

回归平方和U与剩余平方和Q:

回归平方和: 

剩余平方和为:    

F 统计量为:   

1.	#回归平方和U  
2.	U=np.sum((yvals1-ymean)**2)  
3.	Q=np.sum((y-yvals1)**2)  
4.	#剩余平方和Q  
5.	#F检验  
6.	k=4  
7.	n=12  
8.	F=(U/k)/(Q/(n-k-1))  
9.	print(U)  
10.	print(Q)  
11.	print(F)  
12.	print(0.00104*(8**4) - 0.03558*(8**3) + 0.4291*(8**2)- 2.472*8 +8.186) 

答1：在置信水平=0.005上查F分布表知：F0.005(4,12)=6.52。由于166.542>>6.52，所以，土壤侵蚀模数与土壤含氮量之间的四阶回归方程式是显著的。

答2：预测当土壤侵蚀模数x=8000t/(km2*a)时的土壤含氮量:

y=0.00104*(8**4) – 0.03558*(8**3) + 0.4291*(8**2)- 2.472*8 +8.186=1.915(g.m-2)

今天的文章非线性函数模型（多项式拟合）预测土壤侵蚀模数分享到此就结束了，感谢您的阅读。