目标识别的方法和分类_目标识别的方法和分类

现在目标检测、语义分割太火了，方法很重要，但是如何测评不同方法之间的好坏也是需要注意的问题，一个比较完备的任务可以在“水”文章的时候更快（高被引的文章需要量变引起质变…）。一般在各大榜单上采用相同的指标进行比较，本文就来看看都有哪些计算指标，以及其是如何计算的。

前序

几个名词：
TP:真阳类，FP:假阳类，FN:假阴类，TN:真阴类

• Precision,Recall,F1 Score,iou,map都是越大越好，PR曲线越靠近右上角越好。

目标检测中的算法性能评估指标

• 判断标准就是靠IOU的阈值判断，如果IOU大于设定的阈值，判定为positive；

TP:某类被正确检测出来
FP:错分为某类
FN:某类没有被检测出来
TN:目标检测没有这个属性

Precision

$$Precision=\frac{TP}{TP+FP}$$

Recall

$$Recall=\frac{TP}{TP+FN}$$

PR曲线

Accuracy

$$Accuracy=\frac{TP+TN}{TP+TN+FP+FN}$$

IOU

推荐一篇博客，我觉着写的很好传送门
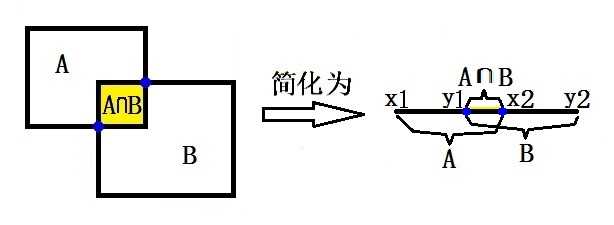
C++代码，参考的Yolo开源代码中的实现方式，由于bbox中记录到的信息是不同的，因此实现方式略有不同。
一维原理图：

C++代码实现：

struct BoundingBox {
	float x1, y1, x2, y2;
	BoundingBox (float a, float b, float c, float d) :x1(a), y1(b), x2(c), y2(d) {}
};
float box_iou(BoundingBox a, BoundingBox b) {
	float xx1 = max(a.x1, b.x1);
	float yy1 = max(a.y1, b.y1);
	float xx2 = min(a.x2, b.x2);
	float yy2 = min(a.y2, b.y2);
	float areaa = (a.x2 - a.x1)*(a.y2 - a.y1);
	float areab = (b.x2 - b.x1)*(b.y2 - b.y1);
	float ovr = max(float(0), xx2 - xx1)*max(float(0), yy2 - yy1);
	return ovr / (areaa + areab - ovr);
}

mAP

直接看一个经典目标检测比赛“The Pascal Visual Object Classes (VOC) Challenge”中如何定义的：

Recall is defined as the proportion of all positive examples ranked above a given rank. Precision is the proportion of all examples above that rank which are from the positive class. The AP summarises the shape of the precision/recall curve, and is defined as the mean precision at a set of eleven equally spaced recall levels [0, 0.1,…,1]:
A P = 1 11 ∑ r ∈ { 0 , 0.1 , . . . , 1 } p i n t e r p ( r ) AP= \frac{1}{11}\sum_{r \in \{0,0.1,…,1\}} p_{interp}(r) AP=111​r∈{
0,0.1,…,1}∑​pinterp​(r)
The precision at each recall level r is interpolated by taking the maximum precision measured for a method for which the corresponding recall exceeds r:
$$p_{interp}(r)=\underset{\tilde{r}:\tilde{r}\ge r}{\max }p(\tilde{r})$$
where $p(\tilde{r})$ is the measured precision at recall $\tilde{r}$.
The intention in interpolating the precision/recall curve in this way is to reduce the impact of the “wiggles” in the precision/recall curve, caused by small variations in the ranking of examples.

全称是：mean average precision，因此为了求解mAP就需要知道每个类别的AP，以及每个类别在不同IOU阈值下的精度的总和，再求均值。
除此之外，还有$mA{P}_{25},mA{P}_{50}$分别表示在IOU阈值为0.25和0.5的条件下的平均精度。

• 代码实现：这里，这里，yolo中应该也有，但是我没找到。其他常见的目标检测框架，COCO中应该也有相应的集成好的实现了！

F1 Score

$$F_1=2\times \frac{P\times R}{P+R}=\frac{2\times TP}{2\times TP+FP+FN}$$

语义分割算法性能评估指标

在语义分割中相当于是多分类的任务，每个点都有自己的类别，那么TP表示的就是真的被分为某类的概率，其他同理。在某个场景中，这里的TP就是正确分割的点数。

Precision

同目标检测的Precision

Recall

同目标检测的Recall

F1 Score

同目标检测的F1 Score

IOU

$$IOU=\frac{正确分为某类的}{被分为该类\cup 被错分成其他类的}=\frac{TP}{TP+FP+FN}$$

检索、位置识别算法性能评估指标

Recall@N

给定一个query的数据，在database中进行搜索（即kdtree，从Scikit-learn或者faiss中都可以），返回N个值，如果在真值文件中存在一个，便认为query是检索正确。
$$Recall@N=\frac{N_{search\_succeed}}{N_{total\_number\_of\_query}}$$

Recall@1%

1%即全部query中的1%个，在不同的database中，其值是动态变化的，在RobotCar中一班Recall@1%就是Recall@5左右的值。

点云配准算法性能评估指标

如果是刷榜，那么两个点云之间是有真值的，$T^{gt}$, $\hat{T}$是算法得到的估计值。两个变换矩阵之间的偏差可以用如下指标来衡量：
$$\Delta T=\hat{T}(T^{gt}{)}^{-1}=\left[\begin{array}{cc}\Delta R& \Delta t\\ 0^T& 1\end{array}\right]$$

旋转误差

$$Erro{r}_R=arccos(\frac{tr(\Delta R)-1}{2}),tr表示矩阵的迹$$

平移误差

$$Erro{r}_t=||\Delta t|{|}_2,||\cdot |{|}_2表示2范数$$

相对平移误差Relative Translational Error(RTE)

RRE是另外一种计算误差的方式，相比于上面计算的旋转误差，应该是等价的。RRE是在Euler角三个分量的绝对误差之和。
$$E_R={\Sigma }_{i=1}^3|\gamma (i)|$$
where $\gamma =F(R_{gt}^{-1}{R}_E)$ is the euler angle of rotation matrix $R_{gt}^{-1}{R}_E$.

相对旋转误差Relative Rotational Error (RRE)

$$E_t=\Vert {\mathbf{t}}_{gt}-{\mathbf{t}}_E{\Vert }_2$$

References

• https://www.cnblogs.com/Tom-Ren/p/11054605.html

今天的文章目标识别的方法和分类_目标识别的方法和分类分享到此就结束了，感谢您的阅读。