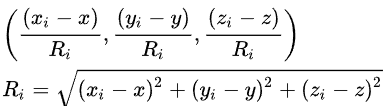精度衰减因子(DOP,Dilution of precision)或精度几何衰减度 (GDOP,geometric dilution of precision)是位置质量的指示器。导航学中,一般用精度因子(DOP)这个概念来表示误差的放大倍数,而GPS接收机通常也会将精度因子随同定位结果一起输出,以供用户参考。它是考虑每颗卫星相对于星座(几何位置)中其它卫星的位置来预计用该星座能得到的位置精度的计算结果。小的DOP值表示强的卫星几何位置和精度的较高概率。高的DOP值表示弱的卫星几何位置和精度的较低概率。
DOP值的通常计算类型如下列出。
- RDOP:相对(relative)位置误差
- PDOP:位置观测值(3D,纬度,经度,高度)
- VDOP:水平观测值(纬度,经度)
- HDOP:高度观测值
- TDOP:时钟差
DOP的值
| DOP | 等级 | 说明 |
|---|---|---|
| 1 | 理想 | 这是用于始终要求尽可能高精度的应用的最高置信水平。 |
| 1~2 | 优秀 | 在此置信水平下,位置测量被认为足够准确,可以满足除最敏感应用之外的所有应用。 |
| 2~5 | 良好 | 表示一个级别,该级别标志着适合于做出业务决策的最低级别。位置测量可用于向用户提供可靠的路线导航建议。 |
| 5~10 | 中等 | 中等位置测量可用于计算,但修复质量仍然可以提高。建议更开阔的天空视图。 |
| 10~20 | 公平 | 位置测量可用于计算,但修复质量仍然可以提高。建议更开阔的天空视图。 |
| >20 | 差 | 在这个级别上,使用精度为6米的设备(50 DOP×6米)测量误差高达300米,应丢弃。 |
DOP值的计算
作为计算 DOP 的第一步,考虑从接收机到卫星 i 的单位向量:
其中 ( x , y , z ) (x,y,z ) (x,y,z)表示接收机的位置, ( x i , y i , z i ) ({ x _{ i } ,y_ { i } ,z_ { i }}) (xi,yi,zi)表示卫星 i 的位置:
A = [ x 1 − x R 1 y 1 − y R 1 z 1 − z R 1 − 1 x 2 − x R 2 y 2 − y R 2 z 2 − z R 2 − 1 x 3 − x R 3 y 3 − y R 3 z 3 − z R 3 − 1 x 4 − x R 4 y 4 − y R 4 z 4 − z R 4 − 1 ] \begin{align} A= \begin{bmatrix} \frac{x_1-x}{R_1} & \frac{y_1-y}{R_1} &\frac{z_1-z}{R_1}&-1\\ \frac{x_2-x}{R_2} & \frac{y_2-y}{R_2} &\frac{z_2-z}{R_2}&-1\\ \frac{x_3-x}{R_3} & \frac{y_3-y}{R_3} &\frac{z_3-z}{R_3}&-1\\ \frac{x_4-x}{R_4} & \frac{y_4-y}{R_4} &\frac{z_4-z}{R_4}&-1\\ \end{bmatrix} \end{align} A=
R1x1−xR2x2−xR3x3−xR4x4−xR1y1−yR2y2−yR3y3−yR4y4−yR1z1−zR2z2−zR3z3−zR4z4−z−1−1−1−1
矩阵 A A A 每行 的前三个元素是从接收器到指示卫星的单位向量的组成部分。每一行的最后一个元素是指伪距 w.r.t. 接收器的偏导数偏差。用最小二乘正规矩阵的协方差矩阵来表示矩阵 Q:
Q = ( A T A ) − 1 Q=(A^TA)^{-1} Q=(ATA)−1
通常情况下: Q = ( J x T ( J d C d J d T ) − 1 J x ) − 1 Q=(J{^T_x}(J_dC_dJ{^T_d})^{-1}J_x)^{-1} Q=(JxT(JdCdJdT)−1Jx)−1其中 J x J_x Jx是传感器测量残差方程 f i f _i fi({ x ‾ \underline{ x } x, d ‾ \underline { d } d) = 0的雅可比(Jacobian)矩阵,对于未知的 x x x, j d \displaystyle j _ { d } jd是传感器测量残差方程相对于测量量 d ‾ { \displaystyle { \underline { d }}} d的雅可比矩阵, C d \displaystyle C_ { d } Cd是测量量中噪声的相关矩阵。对于前面的4个量程测量残差方程:
x ‾ = ( x , y , z , τ ) T {\underline {x}}=(x,y,z,\tau )^{T} x=(x,y,z,τ)T
d ‾ = ( τ 1 , τ 2 , τ 3 , τ 4 ) T {\displaystyle {\underline {d}}=(\tau _{1},\tau _{2},\tau _{3},\tau _{4})^{T}} d=(τ1,τ2,τ3,τ4)T,
τ = c t {\displaystyle \tau =ct} τ=ct, τ i = c t i {\displaystyle \tau _{i}=ct_{i}} τi=cti,
R i = ∣ τ i − τ ∣ = ( τ i − τ ) 2 {\displaystyle R_{i}=|\tau _{i}-\tau |={\sqrt {(\tau _{i}-\tau )^{2}}}} Ri=∣τi−τ∣=(τi−τ)2,
f i ( x ‾ , d ‾ ) = ( x i − x ) 2 + ( y i − y ) 2 + ( z i − z ) 2 − ( τ i − τ ) 2 {\displaystyle f_{i}({\underline {x}},{\underline {d}})={\sqrt {(x_{i}-x)^{2}+(y_{i}-y)^{2}+(z_{i}-z)^{2}}}-{\sqrt {(\tau _{i}-\tau )^{2}}}} fi(x,d)=(xi−x)2+(yi−y)2+(zi−z)2−(τi−τ)2
J x = A , J d = − I {\displaystyle J_{x}=A}, {\displaystyle J_{d}=-I} Jx=A,Jd=−I
并且假设不同 τ i { \displaystyle \tau _{ i }} τi的测量噪声是独立的,这使得测量噪声具有较强的相关性 C d = I {\displaystyle C_{d}=I} Cd=I,这个公式来源于对传感器测量残差方程的一个线性化版本应用最佳线性无偏估计,这个版本是关于当前解 Δ x ‾ = − Q ∗ ( J x T ( J d C d J d T ) − 1 f ) {\displaystyle \Delta {\underline {x}}=-Q*(J_{x}^{T}(J_{d}C_{d}J_{d}^{T})^{-1}f)} Δx=−Q∗(JxT(JdCdJdT)−1f) ,除了 b.l.u.e. C d {\displaystyle C_{d}} Cd是一个噪声协方差矩阵,而不是 DOP 中使用的噪声相关矩阵,DOP 进行这种置换是为了得到一个相对误差。当 C d {\displaystyle C_{d}} Cd是噪声协方差矩阵时, Q Q Q是未知数中由于测量量中的噪声所产生的噪声协方差矩阵的估计。一阶二阶矩(First Order Second Moment,f.o.s.m.)不确定性量化技术是20世纪80年代最先进的估计方法。为了使 f.o.s.m 理论严格适用,要么输入噪声分布必须是高斯分布,要么测量噪声标准差必须相对于解附近输出的变化率小。在这种情况下,第二个标准通常是满足的标准。
这(即对于4次到达/距离测量残差方程)的计算符合[6] ,其中加权矩阵 P = ( J d C d J d T ) − 1 {\displaystyle P=(J_{d}C_{d}J_{d}^{T})^{-1}} P=(JdCdJdT)−1恰好简化为单位矩阵。
注意 : P P P仅仅简化为单位矩阵,因为所有的传感器测量残差方程都是TOA到达时间(伪距)方程。在其他情况下,例如,当试图定位某人在国际遇险频率上的广播时, P P P不会简化为单位矩阵,在这种情况下,除了 TDOP 组成部分或替代 TDOP 组成部分之外,还会有一个“ Frequency DOP”或 FDOP 组成部分。(关于”替代 TDOP 部分”: 由于传统的国际科斯帕斯搜索和营救卫星方案 LEO 卫星的时钟远不如 GPS 时钟准确,放弃其时间测量实际上会提高地理定位解决方案的准确度.
Q {\displaystyle Q} Q的元素被指定为:
Q = [ σ x 2 σ x y σ x z σ x t σ x y σ y 2 σ y z σ y t σ x z σ y z σ z 2 σ z t σ x t σ y t σ z t σ t 2 ] \begin{align} {\displaystyle Q={\begin{bmatrix}\sigma _{x}^{2}&\sigma _{xy}&\sigma _{xz}&\sigma _{xt}\\\sigma _{xy}&\sigma _{y}^{2}&\sigma _{yz}&\sigma _{yt}\\\sigma _{xz}&\sigma _{yz}&\sigma _{z}^{2}&\sigma _{zt}\\\sigma _{xt}&\sigma _{yt}&\sigma _{zt}&\sigma _{t}^{2}\end{bmatrix}}} \end{align} Q=
σx2σxyσxzσxtσxyσy2σyzσytσxzσyzσz2σztσxtσytσztσt2
PDOP、 TDOP 和 GDOP 如下:
P D O P = σ x 2 + σ y 2 + σ z 2 T D O P = σ t 2 G D O P = P D O P 2 + T D O P 2 {\displaystyle {\begin{aligned}PDOP&={\sqrt {\sigma _{x}^{2}+\sigma _{y}^{2}+\sigma _{z}^{2}}}\\TDOP&={\sqrt {\sigma _{t}^{2}}}\\GDOP&={\sqrt {PDOP^{2}+TDOP^{2}}}\\\end{aligned}}} PDOPTDOPGDOP=σx2+σy2+σz2=σt2=PDOP2+TDOP2
注意 GDOP 是 Q Q Q矩阵跟踪的平方根。
水平和垂直精度因子:
H D O P = σ n 2 + σ e 2 {\displaystyle HDOP={\sqrt {\sigma _{n}^{2}+\sigma _{e}^{2}}}} HDOP=σn2+σe2
V D O P = σ u 2 {\displaystyle VDOP={\sqrt {\sigma _{u}^{2}}}} VDOP=σu2
都取决于坐标系的使用。与当地的地平面和当地的垂直方向相对应,分别在北面、东面和坐标系上方。
今天的文章DOP:精度衰减因子( Dilution of Precision)分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/64071.html