泛函分析笔记(十五) Hahn-Banach 定理、闭值域定理

1. Hahn-Banach 定理

实向量空间中： X是实向量空间，p是X上的 次线性泛函 ，即一个满足 $p(\alpha x) = \alpha p(x) \forall a>0,\forall x\in X;p(x+y) \le p(x)+p(y),\forall x,y\in X $ （就是叠加的部分变成小于等于了，所以次了）的函数 $p:X\to \mathbb{R}$ 。
设Y是X的子空间， $l:Y\to \mathbb{R}$ 是Y上的线性泛函，它满足
$$l(y)\le p(y),\forall y\in Y$$
则存在线性泛函 $\tilde{l}:X\to \mathbb{R}$ 满足
$\forall y\in Y,\tilde{l}(t)=l(t),\forall x\in X,\tilde{l}(x)\le p(x)$

赋范向量空间中： X是赋范向量空间，Y是X的子空间，设 $l:Y\to \mathbb{K}$ 是连续线性泛函。
则存在一个连续线性泛函 $\tilde{l}:X\to \mathbb{K}$ 满足 $\tilde{l}(y)=l(y),\forall y\in Y且||\tilde{l}|{|}_{X^{\prime }}=||l|{|}_{Y^{\prime }}$

emmm这个变成范数相等了。

Taylor-Foguel 定理： X是赋范向量空间，则所有定义在X子空间上的连续线性泛函有到X上的唯一保范延拓，其充分必要条件是X的对偶空间 X’是严格凸的。

(知乎这个大佬的对偶空间讲的好形象啊！
怎么形象地理解对偶空间（Dual Vector Space）？ – 马同学的回答 – 知乎
https://www.zhihu.com/question/38464481/answer/235672121)

Bishop-Phelps 定理： X是实Banach空间，设
Y ′ : = { x ′ ∈ X ′ ; ∃ x 0 , ∣ ∣ x 0 ∣ ∣ = 1 且 s u p ∣ ∣ x ∣ ∣ = 1 ∣ x ′ ( ) x ∣ = ∣ ∣ x ′ ( x 0 ) } Y’:=\{x’\in X’;\exists x_0,||x_0||=1 且 sup_{||x||=1}|x'()x|=||x'(x_0)\} Y′:={
x′∈X′;∃x0​,∣∣x0​∣∣=1且sup∣∣x∣∣=1​∣x′()x∣=∣∣x′(x0​)}
则Y’在X’中稠密

(复习一下稠密：

• 如果一个集合与一个元素属于的任意一个开集的交集都非空，那么我们称这个集合对于该元素稠密。
• 如果一个集合是一个空间的子集且对于该空间的任意元素都稠密，那么我们称这个集合在这个空间中稠密。)

1.1. 几何形式的Hahn-Banach定理：凸集的分离

在实赋范向量空间X中，非零线性连续泛函 $l:X\to \mathbb{R}$ 以及一个 $\gamma \in R$ 集合
{ x ∈ X ; l ( x ) = γ } \{x\in X;l(x)=\gamma\} {
x∈X;l(x)=γ}
称作闭仿射超平面，而集合 { x ∈ X ; l ( x ) ≥ γ } \{x\in X;l(x)\ge \gamma\} {
x∈X;l(x)≥γ} 是闭半空间， { x ∈ X ; l ( r ) > γ } \{x\in X;l(r)>\gamma\} {
x∈X;l(r)>γ} 是开半空间。

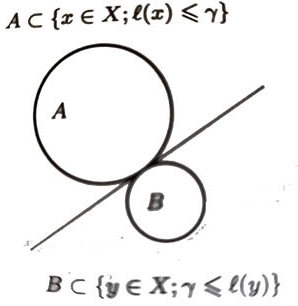
X中有A、B两集合，如果存在一个非0的 $l\in X^{\prime }$ 和 $\gamma \in \mathbb{R}$ 使得
A ⊂ { x ∈ X , l ( x ) ≤ γ } , B ⊂ { y ∈ X ; γ ≤ l ( y ) } A\subset \{x\in X,l(x)\le \gamma\},B\subset \{y\in X;\gamma\le l(y)\} A⊂{
x∈X,l(x)≤γ},B⊂{
y∈X;γ≤l(y)}
即它们被包含在两个闭半空间内，其交集是闭仿射超平面 { y ∈ X ; l ( y ) = γ } \{y\in X;l(y)=\gamma\} {
y∈X;l(y)=γ}
这是集合A和集合B被超平面分离。

凸集的分离： 设A和B是实赋范向量空间X的两个非空子集，满足 $A是开凸集，B是凸集；A\cap B=\varnothing$ 那么存在非零的 $l\in X^{\prime },y\in \mathbb{R}$ 使得 $l(x)\le \gamma \le l(y),\forall x\in A,y\in B$

所有就是说如果两个集合的交集是空集，那么就能找到一个非0的连续泛函使其映射结果不相交。

如果是复向量空间，则存在非零的 $l\in X^{\prime },\gamma \in R$ 使得 $Rel(x)<\gamma \le Rel(y)$

凸集的严格分离： 若A与K是实赋范向量空间X的两个非空子集，满足 A是凸集且是闭集，K是凸集且是紧集，二者交集为空集 ，那么一定存在非零的 $l\in X^{\prime },\gamma \in R,\delta >0$ 使得
$$l(x)\le \gamma -\delta <\gamma +\delta <l(y)$$

依然是分离，而且不能取到恰好等于 $\gamma$

如果是复向量空间，则存在非零的 $l\in X^{\prime },\gamma \in R,\delta >0$ 使得
$$Rel(x)\le \gamma -\delta <\gamma +\delta \le Rel(y)$$

2. Banach 闭值域定理

对偶算子： X和Y是同一数域上的两个赋范向量空间，给定任意算子 $A\in \mathcal{L}(X;Y)$ ，存在唯一的算子 $A^{\prime }\in \mathcal{L}(Y^{\prime };X^{\prime })$ ,称为A的对偶算子或者简称A的对偶，使得
$$A^{\prime }{y}^{\prime }(x)=y^{\prime }(Ax)$$
$$||A^{\prime }|{|}_{\mathcal{L}(Y^{\prime };X^{\prime })}=||A|{|}_{\mathcal{L}(X;Y)}$$

如果一个算子是紧的，那么它的对偶算子也是紧的。

Banach 闭值域定理：

1. 设X与Y是同一数域上的Banach空集， $A\in \mathcal{L}(X;Y)$ 则以下条件等价
   • 算子 $A:X\to Y$ 有闭值域，即 Im A 是Y中的闭集
   • 对偶算子 $A^{\prime }:Y^{\prime }\to X^{\prime }$ 有闭值域，即 $Im{A}^{\prime }$ 是X’中的闭集。
2. X和Y是在同一数域上的Banach空集， $A\in \mathcal{L}(X;Y)$ 则以下条件等价
   • 算子 $A:X\to Y$ 是漫射，即 Im A=Y
   • 存在常数C使得对偶算子 $A^{\prime }:Y^{\prime }\to X^{\prime }$ 满足 $||y^{\prime }||\le C||A^{\prime }{y}^{\prime }||$
   • 对偶算子 A’ 是单射且 Im A’在X’中是闭合的。

今天的文章泛函分析笔记(十五) Hahn-Banach 定理、闭值域定理分享到此就结束了，感谢您的阅读。