洛谷1436棋盘分割

题目描述

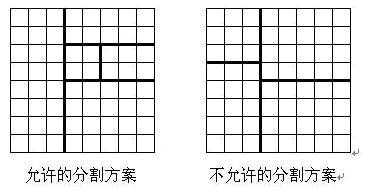
将一个８*８的棋盘进行如下分割：将原棋盘割下一块矩形棋盘并使剩下部分也是矩形，再将剩下的两部分中的任意一块继续如此分割，这样割了(n-1)次后，连同最后剩下的矩形棋盘共有n块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行)

原棋盘上每一格有一个分值，一块矩形棋盘的总分为其所含各格分值之和。现在需要把棋盘按上述规则分割成n块矩形棋盘，并使各矩形棋盘总分的平方和最小。

请编程对给出的棋盘及n，求出平方和的最小值。

输入输出格式

输入格式：

第1行为一个整数n(1 < n < 15)。

第2行至第9行每行为8个小于100的非负整数，表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。

输出格式：

仅一个数，为平方和。

输入输出样例

输入样例#1：

3
1 1 1 1 1 1 1 3
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0
1 1 1 1 1 1 0 3

输出样例#1：

1460

思路：

​ 主要是考验思维吧，只要想到用五维dp就可以很快的推出dp推导式。dp【i】【j】【p】【q】【m】代表左上角坐标（i，j），右下角坐标（p，j）的矩形切m刀的最大值。

然后dp推导式在代码中

代码：

#include <stdio.h>
#include <algorithm>
#include <string.h>
using namespace std;

int maps[10][10];
int sum[10][10] = {0};
int dp[10][10][10][10][15] = {0};

int main () {
    int n;
    scanf("%d", &n);
    memset(dp, 0x3f3f3f3f, sizeof(dp));
    for (int i = 1; i <= 8; i++) {
        for (int j = 1; j <= 8; j++) {
            scanf("%d", &maps[i][j]);
            sum[i][j] = sum[i][j - 1] + maps[i][j];
        }
    }
    for (int i = 1; i <= 8; i++) {
        for (int j = 1; j <= 8; j++) {
            for (int p = i; p <= 8; p++) {
                for (int q = j; q <= 8; q++) {
                    int suu = 0;
                    for (int o = i; o <= p; o++) {
                        suu += sum[o][q] - sum[o][j - 1];
                    }
                    dp[i][j][p][q][0] = suu * suu;
                }
            }
        }
    }
    for (int o = 1; o < n; o++) {
        for (int i = 1; i <= 8; i++) {
            for (int j = 1; j <= 8; j++) {
                for (int p = i; p <= 8; p++) {
                    for (int q = j; q <= 8; q++) {
                        for (int k = i; k < p; k++) {
                            dp[i][j][p][q][o] = min(dp[i][j][p][q][o], dp[i][j][k][q][o - 1] + dp[k + 1][j][p][q][0]);
                            dp[i][j][p][q][o] = min(dp[i][j][p][q][o], dp[i][j][k][q][0] + dp[k + 1][j][p][q][o - 1]);
                        }
                        for (int k = j; k < q; k++) {
                            dp[i][j][p][q][o] = min(dp[i][j][p][q][o], dp[i][j][p][k][o - 1] + dp[i][k + 1][p][q][0]);
                            dp[i][j][p][q][o] = min(dp[i][j][p][q][o], dp[i][j][p][k][0] + dp[i][k + 1][p][q][o - 1]);
                        }
                    }
                }
            }
        }
    }
    printf("%d\n", dp[1][1][8][8][n - 1]);
    return 0;
}

转载请注明出处！！！

如果有写的不对或者不全面的地方 可通过主页的联系方式进行指正，谢谢

今天的文章洛谷1436棋盘分割分享到此就结束了，感谢您的阅读。