【代数语言学巡礼】Lambda-演算在形式语义学的中应用II

【代数语言学巡礼】Lambda-演算在形式语义学的中应用II

现在我们开始讲述$\lambda$-演算的基础知识,包括PC上的$\lambda$-演算和类型论上的$\lambda$-演算;

$\lambda$-演算

$\lambda$-演算最早是由Church(1941)在(The Calculi of Lambda-Conversion. Princeton University)中提出来的,但却是 Montague(1970)才使得它在自然语言的形式语义学研究 发挥重要作用.

我们知道自然语言的语法结构和一阶逻辑结构并非一一对应.通过前面的介绍,我们也 已经知道组合原则是形式语义学的基本要求, 否则根本无法对语义进行形式化的研究.然而,Montague之前的生成语义学家(generative semanticists)以及其它的语义学家们都一直无法 找到合适的方法使得语义学也符合组合原则.因此,尽管形式化方法在自然语言的语法研究 方面取得了很大的进步,在语义学方面却基本是不在场的.这一现象基本持续到Montague(1970).在这篇文章中,Montague在Churuch,Tarski等人工作的基础上,提出了 他自己的类型论的内涵逻辑(Montague’s typed intensional logic),并且把$\lambda$-演算应用到各种 语义组合问题的分析中.可以说,在Montague把$\lambda$-演算引进到自然语言语义学的研究之前, 是不存在现在广为人知的形式语义学这一学科领域.但是,$\lambda$-演算在自然语言问题中的引进, 却带来了语义学研究的革命,并为形式语义学的形成和发展奠定了基础.由此也可知,lambda-演算在形式语义学中有非常重要的地位.

下面将具体介绍$\lambda$-演算中的几个关键概念和步骤,即$\lambda$-抽象($\lambda$-abstraction)规则、$\lambda$还原($\lambda$-reduction 或者说$\lambda$-contraction)以及$\lambda$-转换(\lambda-conversion).这又分为PC上简单的$\lambda$-演算和类型论上的$\lambda$-演算.

PC 上的$\lambda$-演算

简单的$\lambda$-抽象规则

从实质上讲,$\lambda$-抽象一个通过$\lambda$-算子从已给定的谓词或者公式中产生新的复杂谓词的过程.通过增加$\lambda$-抽象规则,PC就可以对表示前面提到的各种词组进行处理.当然,这里的有些词组是需要更复杂的$\lambda$-抽象规则(即用到类型论的抽象规则)才可以表示的.简单的$\lambda$抽象具体如下:

R9:如果 $\phi \in$Form且$v$是一个变元,那么$\lambda v[\phi ]\in$Pred-1.
S9:$\Vert \lambda v[\phi ]{\Vert }^{M,g}$ 是集合S,$D$中所有使得 $\Vert \phi {\Vert }^{M,g[d/v]}=1$成立的d所组成的集合.

这里的$\lambda v[\phi ]$也可以读成“the property of being an v such that $\phi$”,即指使得$\phi$成立的那些个体所具有的性质.当$\lambda$-算子作用的辖域非常清楚时,也可以省略[ ]而记作$\lambda v\phi$ .在 Chruch(1941)中,则记为$\lambda v.\phi$;

注意这里的$\lambda$-算子是应用在个体上的,而它对变元的约束方式也类似于全称量词和存 在量词.同一个$\lambda$-算子不可以同时约束两个不同的变元,而应该再重新引进新的$\lambda$-算子. 如$\lambda xP(x,y)$只对$x$进行约束,如想对$y$也进行约束,则应该再引入一个$\lambda$-算子,如

$$\lambda y[\lambda x[P(x,y)]]$$

例:在下面所有的例子中,我们假定有赋值$g(y)=\text{John}$和解释$I(b)=\text{Bill},I(m)=\text{Mary}$;

i) $\Vert \lambda x[\mathrm{run}(x)]{\Vert }^{M,g}=$ 由所有有跑这个动作的个体所组成的集合;
ii) $\Vert \lambda x[\mathrm{like}(x,b)]{\Vert }^{M,g}=$ 由所有喜欢$\Vert b{\Vert }^{M,g[dx]}($ 即 $I(b),$ 即Bill $)$ 的个体所组成的集合;
iii) $\Vert \lambda x[\mathrm{like}(x,y)]{\Vert }^{M,g}=$ 由所有喜欢 $\Vert \mathbf{y}{\Vert }^{M,g[dx]}($ 即 $g(\mathbf{y}),$ 即John $)$ 的个体所组成的集合;
iv) $\Vert \lambda x[$ fish $(x)\wedge \mathrm{like}(x,b)]{\Vert }^{M,g}=$ 由所有喜欢Bill的鱼所组成的集合;
v) 表示 walks and talks”: $\lambda y[($ walk $(y)\wedge \mathrm{talk}(y))]$;
**vi)**用与表层语法对应的成分表示“Mary walks and talks”:

$$\lambda y[(\mathrm{walk}(y)\wedge \mathrm{talk}(y))](m)$$

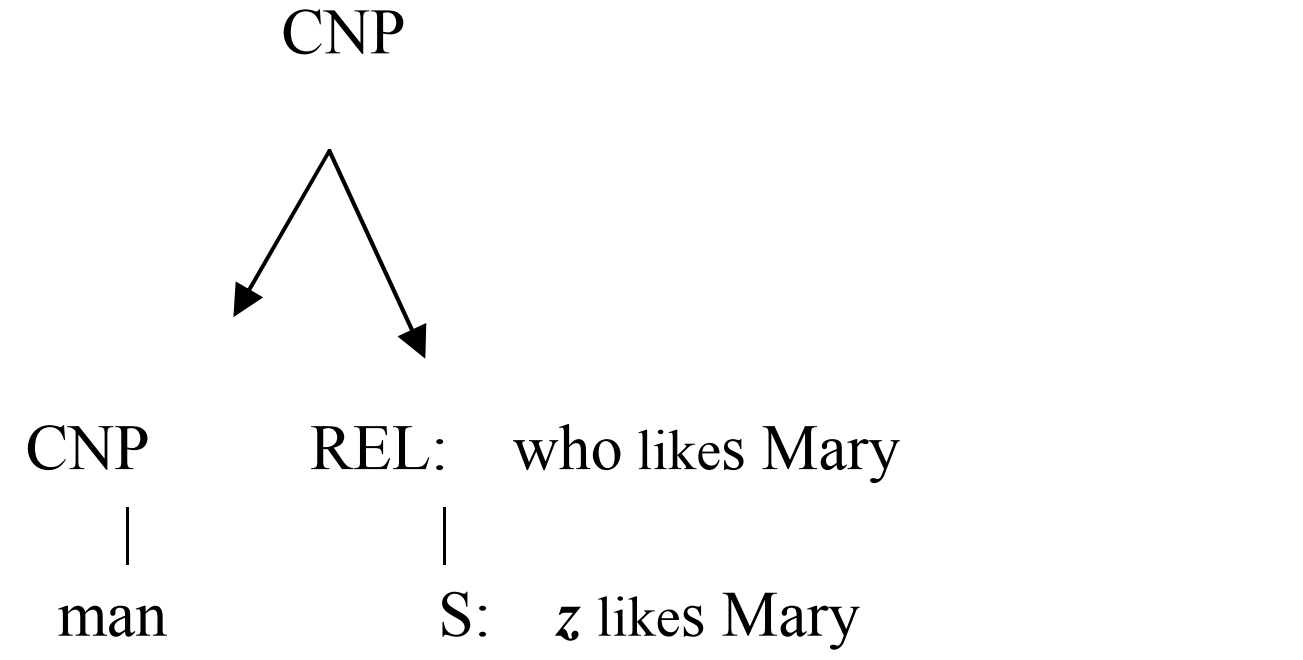
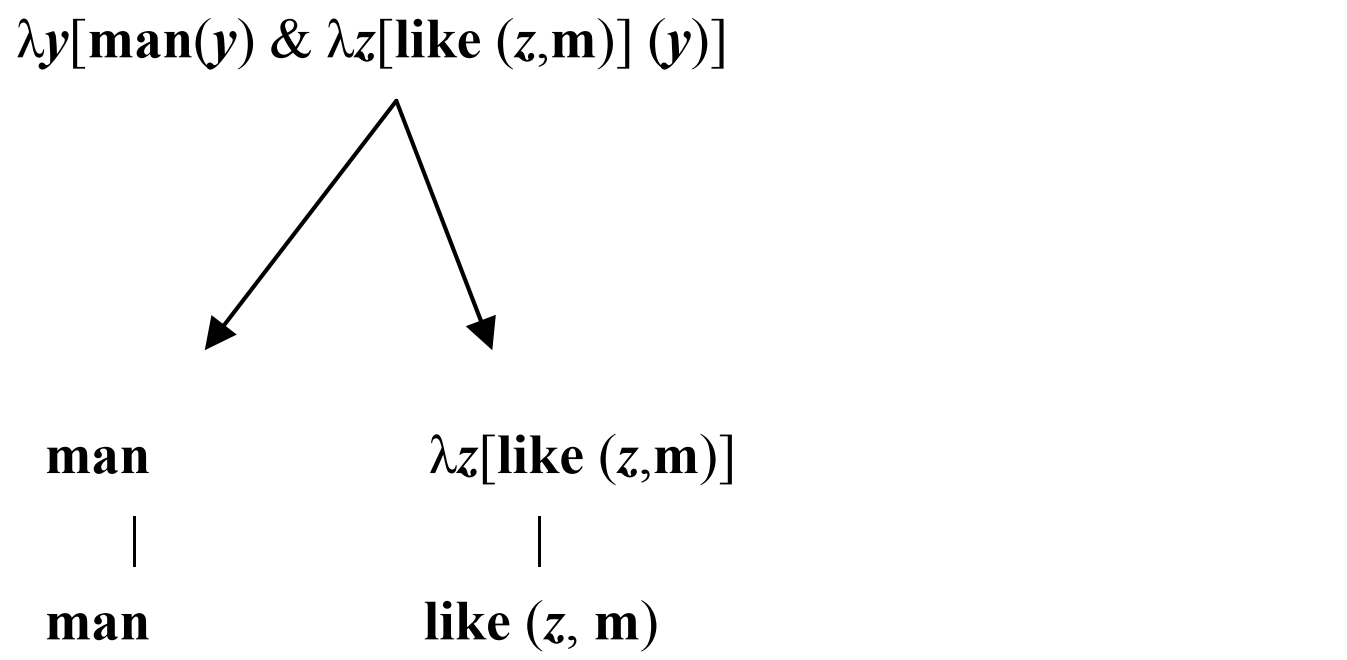
vii) 表示CNP(通名的名词短语)“man who likes Mary”,语法结构如下:

结合CNP与REL(关系从句)的规则:$\lambda y[{CNP}^{\prime }(\mathbf{y})\wedge {REL}^{\prime }(\mathbf{y})]$,把上面的语法结构组合地翻译成$\lambda$-演算(自下而上):

$\lambda$-还原和$\lambda$-转换

$\lambda$-还原是指用定义域中的项代人受$\lambda$-算子约束的变元并消去$\lambda$-算子的过程,这是与$\lambda$抽象相对应的概念.例如,从 $\lambda v[\phi ](t)$得到$\phi [t/v]$就是一个$\lambda$-还原过程,是把$t$代入$\phi$中每一个自由的$v$,而这些$v$又受到$\lambda$-算子的约束. 有了$\lambda$-还原我们就可以直接定义$\lambda$-转换($\lambda$-conversion):

$$\lambda v[\phi ](t)\leftrightarrow \phi [t/v]$$

其中从左到右是一个$\lambda$-还原的过程,而从右到左是一个$\lambda$-抽象的过程.注意,t必须替换$\phi$中的每一个$v$.根据 $\lambda$-转换,我们有:

$\lambda y[(\mathrm{walk}(y)\wedge \mathrm{talk}(y))](m)\leftrightarrow (\mathrm{walk}(m)\wedge \mathrm{talk}(m))$

$\lambda y[\mathrm{man}(y)\wedge \lambda z[\mathrm{like}(z,m)](y)]\leftrightarrow \lambda y[\mathrm{man}(y)\wedge \mathrm{like}(y,m)]$

另外,这里所给的个体上的$\lambda$-表达都十分简单,对于复杂的$\lambda$-表达,其演算规则是类
似的.例如:

$$\begin{array}{l}\lambda x[\lambda y[\lambda z[\varphi (x,y,z)]]](a)(b)(c)\\ \leftrightarrow \lambda y[\lambda z[\varphi (a,y,z)]](b)(c)\\ \leftrightarrow \lambda z[\varphi (a,b,z)](c)\\ \leftrightarrow \varphi (a,b,c)\end{array}$$

需要注意的是,这个式子中的$\lambda$-还原是按从左至右的顺序依次还原的.这也表明“最先经 过$\lambda$-抽象得到的$\lambda$-抽象式在对应的$\lambda$-还原中最后得到还原.其原因是最先得到的$\lambda$-抽象式必定是整个逻辑式中内嵌最深的部分,而$\lambda$-还原总是从最外层的$\lambda$-约束式着手.(参考:蒋严,潘海华,2005,p193)这类似于自动机中一个堆栈(stack)的工作情况,即“先进先出,后入后出”.

在介绍Montague的内涵逻辑(IL)之前,让我们先看一下它与PC的儿个主要不同点:

i) IL有更丰富的类型结构.
ii) 表示函数的表达(function-denoting expressions)在IL中起着非常重要的作用.除基本类型$e$和$t$以外的所有类型都是函数类型(functional types),IL中除$e$和$t$以外的所有表达都指代函数.函数可以不断地进行复合运算,即函数可以是其它函数的变元和函数值.(Functions may serve as the arguments and as the values of other functions. In particular, all relations are also represented as functions.)
iii) IL包含函数的应用(functional application),或者说函数-变元的应用(function-argument application).这在后面的规则中会有具体的例子.
iv) $\lambda$-表达的使用.$\lambda$-算子可以作为构建表示函数的表达的基本工具.
v) 与PC中的一个世界(一个世界或一个模型之间没有什么区别)不同,IL的模型包含一个可能世界集.可能世界在区分内涵和外延中起着重要作用, 且与内涵的类型密切相关.特别是在解释模态算子和指称的模糊性方面,可能世界有重要作用.
vi) IL还包括某种时间结构,这主要用于解释英语中的时态,如在下面描述的过去时态(PAST).

类型和模型结构

类型:

基本类型:$e,t$;
函数类型:如果$a$和$b$是类型,那么$<a,b>$是一个类型(即一个从类型$a$到类型$b$的函数类型)注意,在文献中,$<a,b>$和$a\to b$是等价的标记.
内涵类型:如果$a$是一个类型,那么$<s,a>$是一个类型(一个从可能世界到类型$a$的表达的函数类型);

模型结构:

IL的模型结构:$M=<D,W,\le ,I>$.每个模型必须包含如下四个成分:

• 一个由个体组成的定义域$D$;
• 可能世界集$W$;
• $\le :W$上的关系(也可以理解成是一个时间关系);
• $I$:对所有常元进行赋值的解释函数

类型$a$的表达(相对于$D,W$)的可能指示集可以递归地定义如下:

$D_e=D$;
D t = { 0 , 1 } {D}_{t}=\{0,1\} Dt​={
0,1};
D < a , b > = { f ∣ f : D a → D b } {D}_{<a, b>}=\{f \mid f: {D}_{a} \rightarrow {D}_{b}\} D<a,b>​={
f∣f:Da​→Db​},即所有从$D_a$到$D_b$函数$f$所组成的集合;
D < , a > = { f ∣ f : W → D a } {D}_{<, a>}=\{f \mid f: {W} \rightarrow {D}_{a}\} D<,a>​={
f∣f:W→Da​},即所有从$W$到 $D_a$函数$f$所组成的集合;

IL的语义解释也使用赋值函数$g$的集合 G : { g : G:\{g: G:{
g:任何类型的变元$\to$相应的定义域值$\}$注意:每一个IL的表达都有一个内涵(intension), 内涵是相对应于$M$和$g$而言的;相应的外延(extension)则是相对于$M,w$和$g$.

原子表达、符号和解释

IL的原子表达是常元和变元;每一种类型中都有无穷的常元和变元.Montague引进了一种定义所给定类型的常元和变元的术语,即$c$和$v$,并在下方标记类型和指标.但是,在实际中,人们一般使用更易于记忆的术语.在这里的约定是这样的:

IL的常元用非斜体的黑体字,它们的名称通常表达从被翻译的英语表达如:man,like,等.IL中的变元用斜体的黑体字.这同前面在PC中的符号语言的使用习惯是一样的.其中的类型约定标记如下:

类型e:$w,x,y,z$,以及所有带有上标或下标的类型
类型$<e,t>:P,Q$;
各种关系类型 $<e,<e,t>>:R$;
广义量词类型:$T$常元由模型中的解释函数$I$解释,变元由赋值$g$解释,如规则1.

语法规则和它们的模型论语义解释

IL的语法形式是一个递归定义集,即对所有的类型$a$,”类型a的有意义的表达”的集合$M{E}_a$是IL的语法形式.语义则是给每一个语法规则一个解释;注意: 这里同$PC$一样,其对常元和变元的元语言标记用非斜体的符号.下面是具体的七条语法和相应的语义规则:

原子表达的语法和语义规则

语法规则.1:类型$a$的每一个常元和变元是在$M{E}_a$中的.
语义规则.1:
**(a)**如果$\alpha$是一个常元,那么$\Vert \alpha {\Vert }^{M,w,g}=I(\alpha )(w).$
**(b)**如果$\alpha$是一个变元,那么$\Vert \alpha {\Vert }^{M,w,g}=g(\alpha )$.

注意:递归的语义规则会在给定的模型、世界和赋值下给出每一个表达的外延.如对$\Vert \alpha {\Vert }^{M,w,g}$的解释是在$M$,$w$,和$g$下的,$\alpha$的语义值(外延的);解释函数$I$给每个常元赋予一个内涵,即一个从可能世界到外延的函数;而把这个表示内涵的函数应用到一个可能世界$w$上,则得出了相应的外延.

语法规则.2:(逻辑连接词和算子在公式上的应用,这个同PC类似):

如果$\phi ,\psi {ME}_t$,且$u$任一类型的变元,那么$\neg \phi ,\phi \&\psi ,\phi \vee \psi ,\phi \to \psi ,\phi \leftrightarrow \psi$(也写作$\phi \equiv \psi$),$\exists u\phi ,\forall u\phi ,\square \phi ,\mathrm{PAST}\phi \in {ME}_t$;

语义规则.2:
a)$\neg \phi ,\phi \&\psi ,\phi \vee \psi ,\phi \to \psi ,\phi \leftrightarrow \psi$,$\exists u\phi ,\forall u\phi$同谓词演算一样;
b)$\Vert \square \phi {\Vert }^{M,w,g}=1$当且仅当对所有的$w^{\prime }\in W$,有$\Vert \phi {\Vert }^{M,w^{\prime },g}=1$;
c)$\Vert$ PAST $\phi {\Vert }^{M,w,g}=1$当且仅当存在$w^{\prime }\le w$使得$\Vert \phi {\Vert }^{M,w^{\prime },g}=1$;

语法规则.3:(=):如果$\alpha ,\beta \in {ME}_a$,那么$\alpha =\beta \in {ME}_t$;

语义规则.3:$\Vert \alpha =\beta {\Vert }^{M,w,g}=1$当且仅当$\Vert \alpha {\Vert }^{M,w,g}=\Vert \beta {\Vert }^{M,w,g}$;

下面这两对规则即4和5是针对”up”和”down”算子的,它们对于内涵的理解是非常关键的,简单说明一下;因为这里不打算深入讨论内涵和外延的区分;

从内涵得到外延的规则

语法规则.4(“uр”-operator):如果$\alpha \in {ME}_a$,那么$[{}^{\wedge }\alpha ]\in {ME}_{<s,a>}$;
语义规则.4:KaTeX parse error: Expected ‘}’, got ‘EOF’ at end of input: …pha]\|^{
{M,w,g}是类型$<s,a>$的一个函数$h$使得任何$w^{\prime }\in W$,有$h(w^{\prime })=\Vert \alpha {\Vert }^{M,w^{\prime },g}$;

从外延得到内涵的规则

语法规则.5(“down”-operator):如果$\alpha \in {ME}_{⟨s,a>}$,那么$\left[{}^{\vee }\alpha \right]\in {ME}_a$;
语义规则.5:$\Vert [{}^{\vee }\alpha ]{\Vert }^{M,w,g}$是$\Vert \alpha {\Vert }^{M,w,g}(w)$;

函数变元应用规则(Function-argument application)

语法规则.6:如果$\alpha \in {ME}_{<a,b>}$且$\beta \in {ME}_a$,那么$\alpha (\beta )\in {ME}_b$;
语义规则.6:$\Vert \alpha (\beta ){\Vert }^{M,w,g}=\Vert \alpha {\Vert }^{M,w,g}(\Vert \beta {\Vert }^{M,w,g})$;

Lambda-抽象规则(Lambda-abstraction)

语法规则.7: 如果 $\alpha \in {ME}_a$且$u$是类型$b$的一个自由变元,那么$\lambda u[\alpha ]\in {ME}_{<b,a>}$;
语义规则.7:$\Vert \lambda u[\alpha ]{\Vert }^{M,w,g}$是类型$b\to a$的一个函数$f$使得类型$b$的任一对象$d$,有$f(d)=\Vert \alpha {\Vert }^{M,w,g[d/u]}$;

简单的$\lambda$-抽象规则是应用在个体上的.相比较而言,这里的$\lambda$-抽象规则是应用在类型上的,而且可以是任意复杂度的类型,这大大地增强了用$\lambda$-算子构造复杂的谓词的能力.事实上,我们可以看出,$\lambda$-表达式在某种程度上就是一个函数,如$\lambda v[\alpha ]$就是一个函数,其变元是$v,$而其函数值就是通过$v$的值而具体化的$\alpha$表达式;

例如:$\lambda x\left[x^2+1\right]$表示函数$x\to x^2+1$;

例如:函数变元应用(Function-argument application):$\lambda x\left[x^2+1\right](5)=26$;

与其它函数符号不同的是,$\lambda$-表达式给出了函数的具体名称,而不仅是某个符号,如$f,g$;就$\lambda$-转换而言,其规则同简单$\lambda$-演算中的规则是一样的;

参考文献

[1] Chierchia, Gennaro, and McConnell-Ginet, Sally.2000. Meaning and Grammar: An Introduction to Semantics. Cambridge: MIT Press.
[2] Lambda-演算在形式语义学的中应用I.傅庆芳.
[3] Partee, Barbara H. $2007.$ Formal Semantics and Current Problems of Semantics.

今天的文章【代数语言学巡礼】Lambda-演算在形式语义学的中应用II分享到此就结束了，感谢您的阅读。