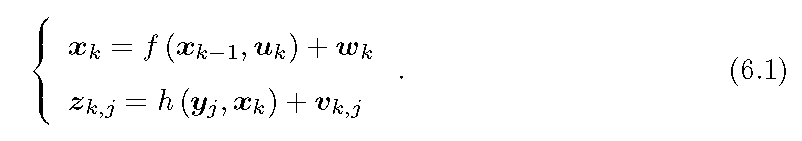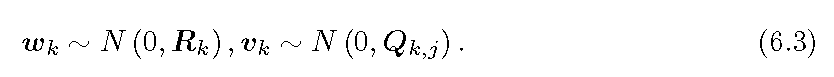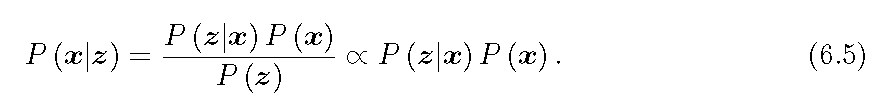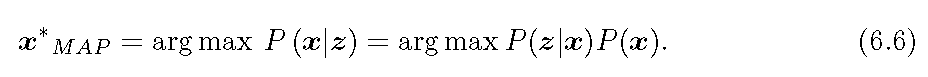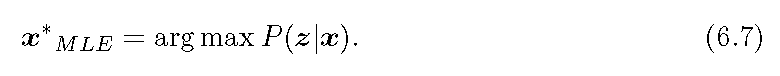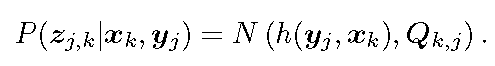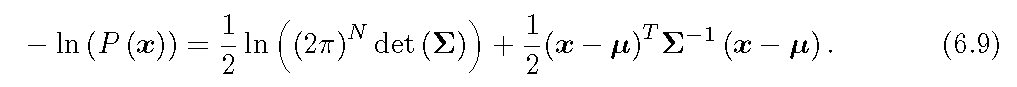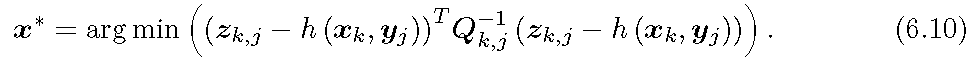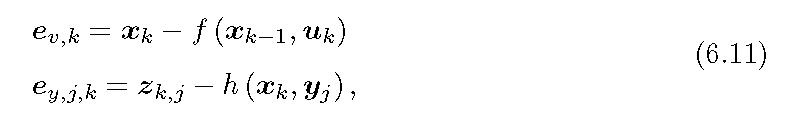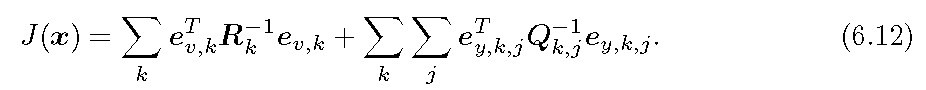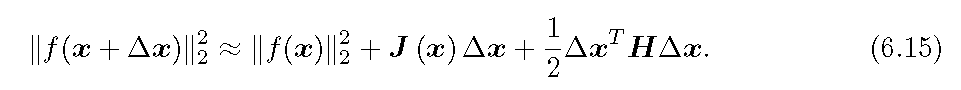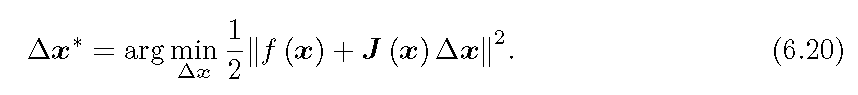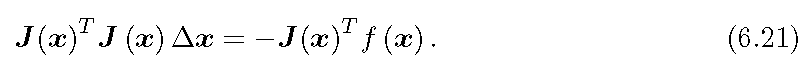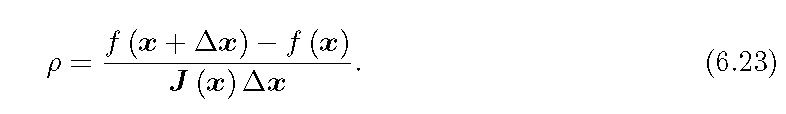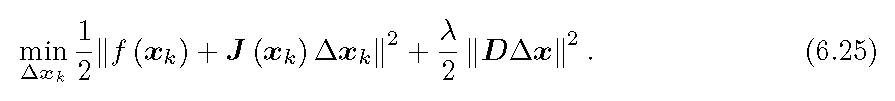视觉 SLAM 十四讲 —— 第六讲非线性优化

根据前几讲已经详细介绍了 SLAM 模型的运动方程和量测方程，其中运动方程中的位姿能够用变换矩阵来描述，而量测方程中的内参随相机固定，外参则是相机的位姿。但是在现实观测中，由于噪声的存在，观测不可能完美的符合方程的描述。因此就需要在计算过程中对噪声污染后的数据进行矫正，从而得到更精准的结果。好在在 SLAM 问题中，同一个点通常会在不同时刻被多次观测，同时每个时刻观测到的点也不止一个，这些限制使得消除噪声的影响称为可能。而这就是经典的状态估计问题。

状态估计问题

最大后验和最大似然

经典 SLAM 模型用状态估计理论能够描述为一个运动方程和一个观测方程的组合

其中运动方程描述了相机位姿随运动造成的变化， $\textbf{x}_k$ 表示相机的位姿。而观测方程描述了在当前位姿下对某个路标的观测结果， $\textbf{y}_j$ 为路标，而观测结果 $\textbf{z}_{k,j}$ 就是在相机位姿为 $\textbf{x}_k$ 时对路标 $\textbf{y}_j$ 所成的像。因此对应观测方程能够表示为

其中 $\textbf{K}$ 为相机的内参矩阵，s 为成像照片相邻像素点的距离。需要注意的是，这里 $z_{k,j}$ 和 $\textbf{y}_j$ 都是齐次坐标，而 6.2 式隐含了一次齐次坐标到非齐次坐标的转换。

最后 $\textbf{w}_k$ 和 $v_{k,j}$ 分别描述了运动噪声和观测噪声，其意义能够被理解为实际控制与预想控制直接的差别和实际观测与现实情况的差别。

而我们最终的目的就是要基于实际的带噪声的观测和控制来估计出相机实际的位姿和地图（路标）。进一步，我们可以设想当相机位姿确定时，将一定能够观测到固定的路标，因此位姿和路标之间本质上存在着某种一一对应关系。这表明我们可以暂时将路标（地图）作为位姿的因变量而融入到观测方程中，而将观测方程直接理解为对位姿的观测。这转换为一个经典的状态估计问题。此时还可以进一步将 $\textbf{u}$ 的影响也作为已知量融入运动方程中，将问题简化为在 $\textbf{z}$ 已知的条件下计算相机位姿 $\textbf{x}$ 的状态分布

这里插一句，如果上述问题忽略观测图片的顺序，而把他们看成是一堆彼此没有关系的图片，这个问题也被称为 Structure from Motion（SfM）。

6.5 式中直接估计概率分布是困难的，但是求一个状态最优的估计使得在该状态下后验概率最大化却是可行的。如此，状态估计问题能够被转换为最大后验概率问题。

其可以被解释为最大化似然概率和先验概率的乘积。举一个实际的例子，当相机观测到某个已知的路标时，那么相机大概率位于路标周围且朝向路标。但如果相机位置先验在此路标周围的概率很大，这也将降低对于相机在路标附近的置信度。

当然，某些情况下，我们可能并没有当前相机位姿的先验，对应问题就转变为最大似然估计问题。

上式直观的理解就是“在什么样的位姿下，最可能产生如下的观测”。

最小二乘的引出

那么如何求解最大似然估计问题呢？我们首先从实际观测的分布入手。由于观测噪声项服从均值为零的高斯分布，如式 6.3 所示，对应观测应服从

通常将最小化如下概率分布转换为最大化其负对数。

而由于第一项与 $\textbf{x}$ 无关，因此上式能够等价为最小化第二项

上式还能够进一步拆分为运动误差和量测误差和的形式，如果定义

那么最小化项变为

这样就得到了一个总体意义上的最小二乘问题。

仔细观察 6.12 式，会发现 SLAM 中的最小二乘具有一些特殊的性质

虽然整体的状态变量维数很高，但由于整个问题的目标函数由许多个误差的（加权的）平方和组成，因此每一个误差项都相对简单，仅与一两个状态变量相关。这样，在把这些误差项的小雅可比矩阵组合成一个大的雅可比矩阵时，对应增量方程的求解会具有一定的稀疏性，使得在大规模时也可以求解。
其实如果直接用变换矩阵进行求解，那么整个问题将是一个约束优化问题（旋转矩阵必须为正交矩阵且行列式为1）。而如果转换为李代数，那么将是一个无约束优化问题，这也体现了李代数的优势。
最后虽然整个推导的结果是一个平方形式（二范数），但这并不是唯一可行的度量方式。如果把二范数理解为欧氏空间中的距离，那么还有很多定义方式能够获得某些特殊的性质和结果。

非线性最小二乘

下面简单介绍以下最小二乘问题的求解。首先一个最小二乘问题能够描述为

其中 $\textbf{x} \in \mathbb{R}^n$ 为一个 n 维向量，是任意非线性函数， $f(\textbf{x}) \in \mathbb{R}^m$ 为一个 m 维向量。

如果是一个简单函数，那么可以直接通过对求导，并比较所有导数为零的点的大小来求解 $\textbf{x}$ 的最小值。但对于 SLAM 问题，我们并不能够顺利地求解对应非线性方程导数为零的点。在此时，通常将采用迭代的方式从一个初始值出发，不断地更新当前的优化变量，使目标函数下降。

下面我们就介绍一下常用的两种迭代方式

一阶和二阶梯度法

为了获取每一个有效的更新量，最直观的想法就是对函数在当前位置进行泰勒展开

其中 $\textbf{J}(x)$ 是 $\left \| f(x) \right \|^2$ 关于 $\Delta x$ 的一阶导数雅可比矩阵， $\textbf{H}$ 是二阶导数海塞矩阵。如果只保留一阶近似，那么对应更新增量为其被称为最速下降法，因为其每一步都选取下降最快的方向进行更新。而如果保留二阶近似，对应更新增量为的解，其被称为牛顿法。

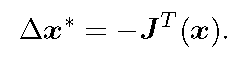
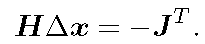
由于泰勒展开已经将复杂的非线性方程转换成了多项式的形式，因此整体求解相对简单。不过最速下降法过于贪心，容易走出锯齿路线，反而增加了迭代次数。而牛顿法又需要计算海塞矩阵，在规模较大时十分困难。因此实际中通常采用的是高斯牛顿法和列文伯格-马夸尔特法。

高斯牛顿法

高斯牛顿法是最优化算法中最简单的方法之一。它不再对二次项进行泰勒展开，而是对原始 f(x) 进行泰勒展开，然后通过代数运行对二次项进行分析。由此，对应保留一阶近似，高斯牛顿法目标函数如下

对其进行代数运算，并对 $\Delta x$ 求导，最后令导数为零，可以得到如下方程

它本质是一个线性方程，也被称为增量方程，或者高斯牛顿方程，或者正规方程。如果仿照上面二阶方法的形式，令

$\textbf{J}(x)^T\textbf{J}(x)=\textbf{H}$ ， $-\textbf{J}(x)^Tf(x)=g$

将得到与二次法相同的形式。

从中我们可以得出以下分析：

高斯牛顿法通过 $\textbf{J}(x)^T\textbf{J}(x)$ 来近似海塞矩阵的计算，从而简化了计算量
上式中要求 $\textbf{H}$ 矩阵必须使正定矩阵，但是 $\textbf{J}(x)^T\textbf{J}(x)$ 只具有半正定的特性，这导致算法稳定性较差，不太容易收敛
最后，即使 $\textbf{J}(x)^T\textbf{J}(x)$ 满足非奇异也非病态，如果我们选取的步长太大，同样可能因为近似程度不够而导致无法收敛

列文伯格-马夸尔特方法

为了解决上述高斯牛顿法存在的问题，列文伯格-马夸尔特方法在此基础上进行了改进。

为了解决高斯牛顿法可能存在的近似不准确的问题，列马方法引入了一个信赖区域的概念，通过下式进行度量

其可以理解为函数实际偏差与估计偏差的比值。如果值比较大，则认为实际下降比预计下降还要大，因此可以放大近似范围；如果值比较小，那么认为此时的估计是不准确的，应该减小近似范围。整个算法的流程如下

上述的具体参数都是经验值，实际应用中可以进行调整。

最后上述 6.24 式的求解，采用拉格朗日乘子法将其转换为一个无约束优化问题

其对应的解具有如下形式

从上式可以得出以下分析

相比于高斯牛顿法，通过引入限制调整，高斯牛顿法其实是列马方法的子集。当 $\lambda$ 比较大时，列马方法更接近于一阶梯度下降法；而 $\lambda$ 比较大时，则更接近高斯牛顿法。这可以理解为列马方法在一阶和二阶近似之间寻找一个平衡。
通过 $\lambda$ 的引入也部分解决了可能存在的 $\textbf{H}$ 半正定的问题，提高了算法的稳定性。

g2o：图优化理论简介

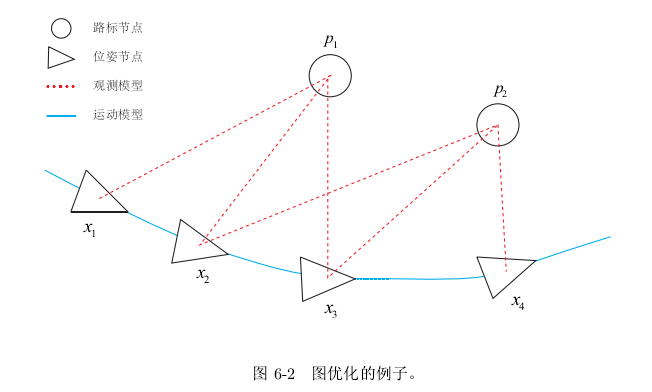
图优化是把优化问题表现成图的一种方式。一个图由若干个顶点（vertex）和边（edge）组成。进而，用顶点标识优化变量，用边表示误差项。于是，对任意一个上述形式的非线性最小二乘问题，我们可以构建与之对应的一个图。

我们用三角形表示相机位姿节点，用圆形表示路标点，它们构成了图优化的顶点；同时，蓝色线表示相机的运动模型，红色虚线表示观测模型，它们构成了图优化的边。此时，虽然整个问题的数学形式仍是式（6.12）那样，但现在我们可以直观地看到问题的结构了。如果我们希望，也可以做去掉孤立顶点或优先优化边数较多（或按图论的术语，度数较大）的顶点这样的改进。但是最基本的图优化，是用图模型来表达一个非线性最小二乘的优化问题。而我们可以利用图模型的某些性质，做更好的优化。

小结

这里只介绍最常见的两种线性优化策略——高斯牛顿和马列方法。其实最优化是处理很多实际问题的基本数学工具，不光是在视觉SLAM中起着核心作用，在类似于深度学习等其他领域，它也是求解问题的核心方法之一。

同时，实际上非线性优化的所有迭代求解方案，都需要用户提供一个良好的初始值。由于目标函数太复杂，导致在求解空间上的变化难以琢磨，对问题提供不同的初始值往往会导致不同的计算结果。这是非线性优化的通病：容易陷入局部极小值。在SLAM问题中，我们会用ICP，PnP 等算法来提供一个更合理的初始值。

最后对于增量方程的求解，由于涉及矩阵的求逆运算，同时SLAM中特征的维数通常很大，因此实际使用过程中几乎没有方法直接对这个高维矩阵求逆。针对SLAM，由于矩阵往往具有特定的稀疏形式，这就为实时求解提供了可能。

Python 示例代码

import numpy as np

f = lambda x, a, b, c: a*x*x + b*x + c

def generate_data(u=0, sigma=1, N=100):
    a, b, c = 10, 25, 10
    x = np.linspace(0, 1, N)
    y = f(x, a, b, c) + np.random.normal(u, sigma, size=(N))
    return x, y
    

def gauss_newton():
    N, sigma = 1000, 10
    inv_sigma = 1 / sigma
    x, y = generate_data(sigma=sigma, N=N)
    theta = np.array([-1, 2, 1.]).reshape((-1, 1))
    iter_num = 1000

    for i in range(iter_num):
        H = np.zeros((3, 3))
        b = np.zeros((3, 1))

        error = y - f(x, *theta)
        J = np.vstack([-x*x, -x, -1 * np.ones_like(x)])
        H = inv_sigma * inv_sigma * J @ J.T
        b = -inv_sigma * inv_sigma * np.sum(np.repeat(error.reshape((1, -1)), 3, axis=0) * J, axis=1).reshape((3, -1))

        cost = np.sum(error * error)

        delta = np.linalg.inv(H) @ b
        theta += delta
        
        print(f"iter: {i}; theta: {theta.T.tolist()}; cost: {cost}")
        return


def gradient_descent():
    N, sigma = 10000, 1
    x, y = generate_data(sigma=sigma, N=N)
    theta = np.array([-1, 2, 1.])
    iter_num = 10000
    lr = 1e-5

    for i in range(iter_num):
        error = y - f(x, *theta)
        theta[0] += np.sum(error * x * x) * lr
        theta[1] += np.sum(error * x) * lr
        theta[2] += np.sum(error) * lr

        cost = np.sum(error * error)
        print(f"iter: {i}; theta: {theta.tolist()}; cost: {cost}")


if __name__ == '__main__':
    gradient_descent()

今天的文章视觉 SLAM 十四讲 —— 第六讲非线性优化分享到此就结束了，感谢您的阅读。

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容，请发送邮件至举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/66356.html

视觉 SLAM 十四讲 —— 第六讲 非线性优化