图形大小_钱志亮：抓住4～6岁图形建构关键期，为孩子小学数学打好基础

西安某个非常杰出的幼儿园园长曾告诉我：当年数学尽管考高分，但绝对就是背题，老师讲过的、自己做过的题目一条条都很辛苦地背下来，每次考试都先把相关定理公式默写在草稿纸上，然后再做题。

顶着家人巨大的压力，无论如何也上不了高中，毅然选择了幼教。直到后来陪儿子上初中课外辅导班的时候，随班跟着听课才弄明白几何的那些事情，恍然大悟原来是这么回事儿。

确实有不少人在几何方面不“开窍”，书上讲圆柱体侧面展开之后是个长方形，尽管老师做了演示，可还是想不通：“明明是个圆的，怎么可能是长方形呢？”。

现实中好多孩子到了初中之后，三角形全等、三角形相似等内容确实完全理解不了。这主要与4～6岁图形建构关键期时练习不够相关。

一、几何图形

孩子从来到世间的那一刻就开始感知图形了，图形无处不在，与我们的生活息息相关，生活中到处都有几何图形，几何图形是所有图形的总称。我们能看见的一切都是由点、线、面等基本几何图形组成的。

几何图形包括平面图形与立体图形，点、直线、线段、射线、三角形、四边形等为平面图形；长方体、圆球、圆锥等为立体图形。

二、拓扑空间关系

客观世界中的各种物体不仅在形态上表现出区别于其他事物的独特性，而且还在空间存在形式上表现出基本的拓扑空间关系(拓扑学是数学的一支学科，它是研究空间形式不变性的科学。

在拓扑几何中，图形在形状上是柔性的，把三角形、正方形的角压进去就都变成了圆形，因此，我们原先在欧式几何中认为各不相同的圆形、正方形、三角形，在拓扑学中都是等价的封闭图形)。

皮亚杰关于儿童认识空间的实验研究认为，学前儿童最初的空间概念正是拓扑学里的空间关系，然后才是欧氏几何和投影几何，这说明儿童的空间概念和几何概念是紧密联系的。

在拓扑学中存在着四种基本的空间关系：邻近关系、分离关系、次序关系、包围关系，用人脸五官的位置来理解，则眼睛和鼻子、鼻子和嘴巴的关系都是邻近关系；眼睛和嘴巴因鼻子而分离，所以它们是分离关系；眉毛、眼睛、鼻子、嘴巴自上而下顺序排列存在着一定的次序关系，且不能相互颠倒；而五官被脸庞的曲线包围起来则是包围关系。

其实，不仅人的五官位置是如此，只要稍稍留意一下我们周围的物体，都不难发现事物与事物之间的这四种关系比比皆是。

就拓扑学来说，无论把图形做怎样的拉扯或压缩，图形原来的空间关系不会改变，这就像一团元宵面包着一团豆沙馅，无论你把元宵搓成个鸭蛋形还是一个桃子形甚至将它压成饼子，馅可能也会随着挤压而变形或移动位置，但面包着馅的拓扑关系不会改变。

图形信息具有两个特点：

1.图形信息是具体的，而非抽象的。

比如，“家具”属于抽象的信息，而桌子、椅子是具体的，可被描述的信息。幼儿在学前期，尤其在学前初期，只能掌握这些具体、形象的信息，认知活动围绕这些具体信息展开。

2.图形信息是直观的，能够很快被人们感知到的。

学前期的儿童通过动作、行为直接感知这种直观信息，进行学习和其他活动处理图形信息的能力我们称之为图形能力。图形能力处理的是具体、形象、可直接感知的信息。

三、图形能力

图形能力包括图形认知能力、图形记忆能力、图形发散思维能力、图形聚敛思维能力以及图形评价能力。

其中，图形认知能力作为其他图形能力的基础，是指发现、了解、识别图形信息的能力，是吸收新信息和利用以前接触过的信息的能力。

吉尔福特将图形认知能力分为图形单元认知、图形类别认知、图形关系认知、图形系统认知、图形转换认知及图形蕴涵认知能力。

随着幼儿的年龄增长，我们所培养幼儿的图形认知能力，从单体认知、类别、关系认知发展到更进一步的系统、转换等认知，并从图形认知能力发展到图形评价、图形发散思维和图形聚敛思维等方面的能力。

皮亚杰让儿童触摸隐藏的实物，然后要求其在另堆实物中指认出相同者或画出实物的外形。根据结果提出了儿童图形知觉发展的三个阶段：

第一阶段(2～4岁)

第一阶段能分辨开放图形和封闭图形，但不能分辨欧氏图形。儿童的典型行为是用手顺着实物的四周轮廓描摩，把手指穿入洞中分离它、这些对物体外围界限的知觉，注意其是否开放、封闭或分离，属于拓扑几何的性质。

第二阶段(4～6岁)

第二阶段是过渡期，能辨认欧氏图形，即区分直线图形(正方形、长方形、平行四边形、菱形)和曲线图形(圆形、椭圆形)。儿童用眼和手跟随图形的边围，并辨识角。

第三阶段(7岁左右)

第三阶段具有逆向思考能力，能辨识直线形成的封闭图形。辨识图形时，由某一固定参考点开始，较有计划和系统性。

在小班时，幼儿还没法画出直线图形，但上了中班，这点要求对他们来说已经不再是困难了，到上大班的时候，他们已能认识各种各样的平面图形和各种几何体。

他们在玩几何图形片和搭积木的过程中，巩固着以前获得的有关空间概念，如上面、下面、里面、外面……体验着一片片或一块块(即部分)与拼搭出的整个物体(及整体)之间的关系；又在“需要几块就拿几块”的规则执行中，巩固着数的概念；其空间想象能力和创造性也在此时得到进一步发展，想到用直角三角形积木拼成木砖。

由于图形比起数来要具体、直观得多——图形是提供儿童连接数学与真实世界的一个最佳机会，五岁至六岁的孩子在幼儿园学习图形构建，为他们进入小学学习数学打下了坚实基础。

四、图形建构关键期

蒙台梭利认为，儿童在每个特定时期都有一种特殊的感受能力，这种感受力促使他对环境中的某些事物甚为敏感，对有关事物注意力很集中、很耐心，而对其他事物则置若罔闻。

她认为这种注意不是出于单纯的好奇，而是在一定的时期由于本能与特定的外部特征之间的密切联系而产生的一种兴趣，是从无意识深处产生出来的一种热情，又由于满足了需要而得到快乐，增强了自己的力量。

蒙台梭利还试图对儿童的敏感期加以区分，提出儿童从出生到5岁是感觉的敏感期；4～5岁是数学概念的敏感期，5～6岁是数学逻辑的敏感期。

在图形方面通过正确认识圆形、正方形、三角形以及长方形、半圆形、椭圆形和梯形，且能逐步理解平面图形的基本特征；能逐步做到图形守恒，不受图形的大小、摆放位置的影响，正确地辨认图形；能对相似的平面图形加以比较，理解图形之间的简单关系；对平面图形的组合拼搭活动表现出较高的积极性以及一定的创造性。

5～6岁的幼儿还能够理解一种图形的典型特征，并在头脑中形成某种图形的“标准样式”，从而进行正确的判断；能进一步理解图形之间较复杂的组合关系。例如：长方形与三角形、梯形之间的组合关系。

学前阶段的儿童各种感觉特别敏感，处在各种感觉的敏感期，在这一时期如不进行充分的感觉活动，长大以后不仅难以弥补而且还会使其整个精神发展受到损伤。

蒙台梭利认为，必须对幼儿进行系统的和多方面的感官训练，使他们通过对外部世界的直接接触，发展敏锐的感觉和观察力。

五、强化训练

幼儿园对儿童进行几何图形启蒙教育，是促进儿童逻辑思维能力和空间想象能力发展的重要起点，而逻辑思维能力是人才素质最重要的、也是最基本的素质之一。

儿童生活在具有各种形状的物体的自然环境和社会环境中，他们早就对物体的大小、形状感兴趣，在游戏中喜欢寻找各种形状的玩具。

但儿童要获得几何形状的初步概念，发展逻辑思维能力和空间想象能力，需要成人和教师的正确引导及科学的教育方法。

① 认识几何形体

几何形体包括平面图形和立体图形两大类。平面图形是由同一平面内的点、线、面所构成的图形，如圆形、正方形、三角形、长方形、椭圆形、梯形等。立体图形则是由空间非同一平面内的点、线、面及其组合而成的图形，如球体、圆柱体、长方体、正方体等。

几何形体中的点没有大小，线没有长短粗细，面没有厚度，体是指形状大小。点、线、面体四者的关系是线与线相交于点，面与面相交于线，体由面包围而成。各种图形都有相应的定义来确定：

圆形：即平面内与一个定点的距离等于定长的点的集合，这些点围成了个封闭的曲线。如瓶口、碗口、圆盘、车轮等物体的轮廓。

三角形：是由三条线段围合而成的封闭曲线。其中若按角的特征来分，可分为锐角三角形、直角三角形、钝角三角形；若按边的特征来分，又可分作不等边三角形、等腰三角形、等边三角形。如乐器中的三角铁、测量工具中的三角尺、房屋山墙上部的房顶等物体轮廓。

正方形：是有一个角是直角且有一组邻边相等的平行四边形。如方手帕、方瓷砖、方桌面、方画框、方窗框等物体的轮廓。

长方形：是有一个角是直角的平行四边形(两组对边分别平行的四边形)。如通常见到的书、门、长纸盒、长桌面等物体的轮廓。

② 建立图形关系

图形关系包括了认识平面图形之间关系的要求和认识平面图形与几何体之间关系(即平面图形如何围合成几何体)的要求。而平面图形之间的关系又有两方面的含义：

一是指图形之间组合或分解的关系：几个直线图形或带直线边的曲线图形可以拼成一个大的图形。

同样，一个任意图形(或直线图形或曲线图形)又可分解成几个相同的或不同的图形。例如，一个轴对称的图形(如梯形)可以等分成两个一样大的相同图形或几个不同的图形；一个中心对称的图形(如正方形)可以等分为几个一样大的相同图形或几个不同图形。

二是指比较相似图形的区别，如两个相似图形，基本形状不变，角的大小也不变；只有边长变了，图形就被放大或缩小了，在比较中体验其中的相互联系。

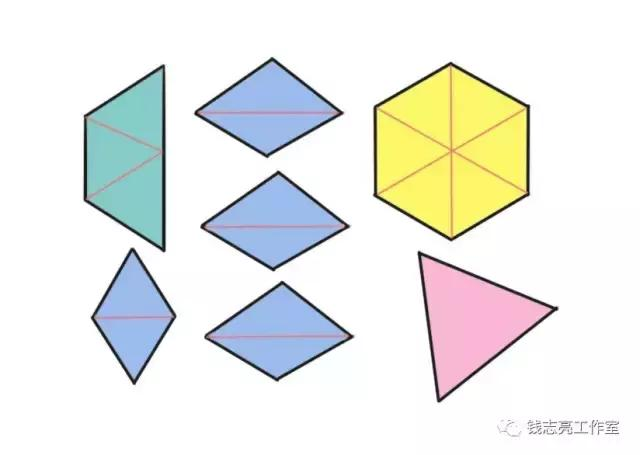
如在玩几何图形活动中，教师让儿童想想利用几何图形可以怎么玩。幼儿经过思索和想象，会给几何图形分类、排序，还会用几何图形进行拼图、游戏等。如把正方形、圆形、三角形、长方形的纸拼搭出小狐狸。

在儿童操作前，教师提出启发性的问题：小狐狸的头形是什么样的，让儿童脑海里有小狐狸的形状。然后让儿童进行拼搭的活动。儿童的探索实践说明，虽然提供的材料是相同的，但是儿童操作的结果却是多样的，通过操作可以充分发挥儿童的创造性想象，又可以培养儿童多角度思考问题的能力。

要引导幼儿能把物体零散部分构成一个整体：即发现物体(或图形)部分和整体的相互关系，要求将幼儿的注意引向拆零部分与整体联系的线索上，发展其空间关系和对图形的心理旋转能力。

③ 逐渐抽象化

爱因斯坦说过：“想象力比知识更重要，因为知识是有限的，而想象力概括着世界上的一切，推动着进步，并且是知识进化的源泉。”

人的创造性思维都需要借助想象，空间想象能力是指人们对客观事物的空间形式进行观察、分析和抽象的能力，是逻辑思维与几何知识及相关技能、经验的融合。

儿童的认知水平往往还停留在事物的表面，对简单的、直观的、平面的图形比较容易理解，而将复杂图形转换为简单图形，相对比较难。

学龄前儿童的想象具有随意性，幻想的成分较多。我们培养儿童的想象思维，要注意鼓励儿童进行各种猜想和幻想，让他们大胆地去想。

要培养儿童空间想象能力，就要丰富幼儿头脑中的表象。现在的儿童绝大多数是从家到学校，没有生活经验缺乏感性认识，头脑中积累的表象并不丰富。

教学中教师必须有意识地通过大量教具、挂图、参观、多媒体教学手段等直观教学扩大儿童的感性认识，使其积累大量的表象。让幼儿在实际玩弄教具的过程，指导幼儿观察，了解其明显的外形特征，然后概括出名称。这样，幼儿在观察中不仅获得了丰富的知识，同时也发展了思维能力。

例如，教幼儿理解“二等分”的含义时，可以渗透几何形体启蒙教育。教师可以拿一块正方形的纸进行演示，先把它对折，等分成两个同样大的长方形。教师边等分，边指导幼儿观察教师怎样把一个正方形分成两个长方形。同时让幼儿观察和比较被分成的两个长方形是不是完全相同。

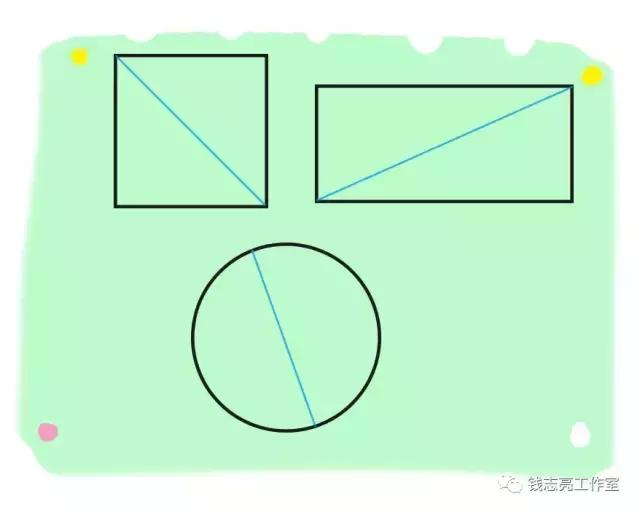
然后教师还可以用同样的方法向幼儿演示把长方形和圆形等分的过程。最后使幼儿在直接感知的基础上，通过思考知道，把一个图形分成两个完全相同的图形，就是二等分。

④ 图形创意

图形创意是指通过一种形态的变化将某种社会事物浓缩成一种视觉的符号，标记和代码，而使之成为一种具有政治、经济、文化或生活价值的东西，并以此来表现任何主体。

简单的表述就是利用日常生活中能够见到的普通事物的特性进行相关联想，并创造出现实中不存在的符号化的图形，如单位的标识。

图形作为一种人与人交流的语言应该被幼儿熟悉，并且能够学会应用。我们知道，思想、情感、信息都是一种抽象的形态，看不见，摸不着。

人们在进行思想情感交流时，需要用一种可以被我们的感官感知的物质形态来负载抽象形态的意义，这样才能实现交流过程。

图形的实质是一种视觉符号，如红灯代表停止，v字的手势代表胜利，商标代表了某种产品品牌，麦当劳的M标志就是一个符号。

幼儿绘画中也会出现大量的符号化的形象。例如，会用简单一个圆下面加个“介”字表示人、两个三角形组成的小鱼，都是在幼儿心中的“符号”。这样简单的图形就能表达幼儿对于绘画的基本需要。

作者｜钱志亮，北京师范大学名师。86级毕业留校，1994年留学归国，博士学历。研究方向为儿童发展问题咨询、特殊需要儿童教育。微信公众号：钱志亮工作室(ID：qzlgzs)