STL源码刨析_宾州中文树 源码剖析

1. STL概述

STL起源：

为的就是复用性的提升，减少人力资源的浪费，建立了数据结构与算法的一套标准。

STL所实现的、是依据泛型思维架设起来的一个概念结构。这个以抽象概念〔 abstract concepts）为主体而非以实际类(classes）为主体的结构，形成了一个严谨的接口标准。在此接口之下，任何组件都有最大的独立性，并以所谓迭代器〈 iterator）胶合起来，或以所谓配接器(adapter）互相配接，或以所谓仿函数( functor）动态选择某种策略（ policy或strategy) 。

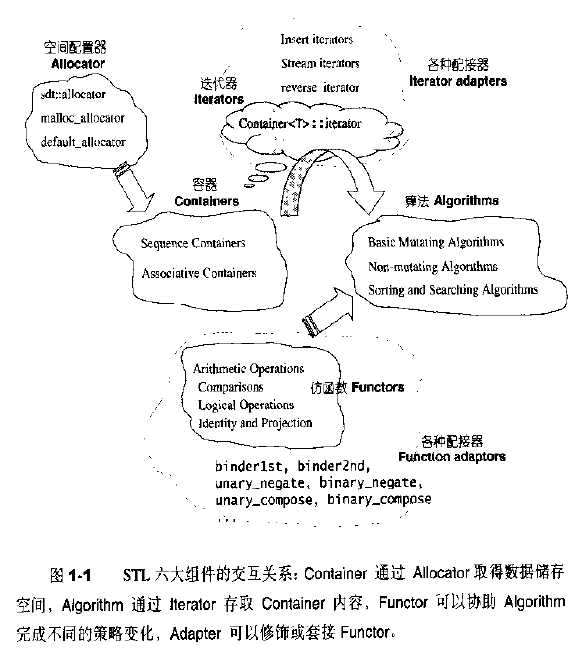
STL六大组件

STL提供六大组件，彼此可以组合套用

1. 容器（containers）：各种数据结构， 如vector, list, deque, set, map用来存放数据，从实现角度是一种class template，提供一个模板类。
2. 算法（algorithms）：各种算法如sort,search, copy, erase…，从实现的角度来看，STL算法是一种function template。
3. 迭代器（iterators）：扮演容器与算法之间的胶合剂，是所谓的“泛型指针”，共有五种类型。从实现角度来看，迭代器是一种将operator*, operator->, operator++, operator–等指针相关操作给以重载的class template。所有STL容器都附带有自己专属的迭代器。
4. 仿函数（functors）：行为类似函数，可作为算法的某种策略（policy）。从实现角度来看，仿函数是一种重载了operator()的class 或 class template。一般函数指针可视为狭义的仿函数。
5. 配接器（adapters）：一种用来修饰容器（containers）或仿函数（functors）或迭代器（iterators）接口的东西。例如，STL提供的queue和stack，虽然看似容器，其实只能算是一种容器配接器，因为它们的底部完全借助deque、所有操作都由底层的deque供应。改变 functor接口者，称为function adapter;改变container接口者,称为container adapter;改变iterator接口者，称为iterator adapter。配接器的实现技术很难一言以蔽之。
6. 配置器（allocators）：负责空间配置与管理，从实现了动态空间配置、空间管理、空间释放的class template。

2. 空间适配器（allocator）

以STL 的运用角度而言，空间配置器是最不需要介绍的东西，它总是隐藏在一切组件（更具体地说是指容器，container）的背后，默默工作，默默付出。但若以 STL 的实现角度而言，第一个需要介绍的就是空间配置器，因为整个STL 的操作对象（所有的数值）都存放在容器之内，而容器一定需要配置空间以置放资料。不先掌握空间配置器的原理，难免在阅读其它STL组件的实现时处处遇到挡路石。

为什么不说allocator是内存配置器雨说它是空间配置器呢?因为空间不一定是内存，空间也可以是磁盘或其它辅助存储介质。是的，你可以写—个allocator,直接向硬盘取空间。

总而言之，空间适配器分为第一级配置器（大内存）和第二级配置器（小内存），通过合理使用和回收内存来达到高效的空间使用。

3.迭代器（iterators）

不论是泛型思维或STL的实际运用，迭代器（iterators）都扮演着重要的角色。STL的中心思想在于:将数据容器（ containers）和算法 （ algurithms）分开，彼此独立设计，最后再以一帖胶着剂将它们撮合在一起。容器和算法的泛型化，从技术角度来看并不困难，C++的class templates和 function templates可分别达成目标。如何设计出两者之间的良好胶着剂，才是大难题。

迭代器是一种smart pointer

迭代器是一种行为类似指针的对象,而指针的各种行为中最常见也最重要的便是内容提领(dereference）和成员访问( member access),因此，迭代器最重要的编程工作就是对operator* 和operator->进行重载（ overloading）工作。关于这一点，C++标准程序库有一个 auto_ptr可供我们参考。

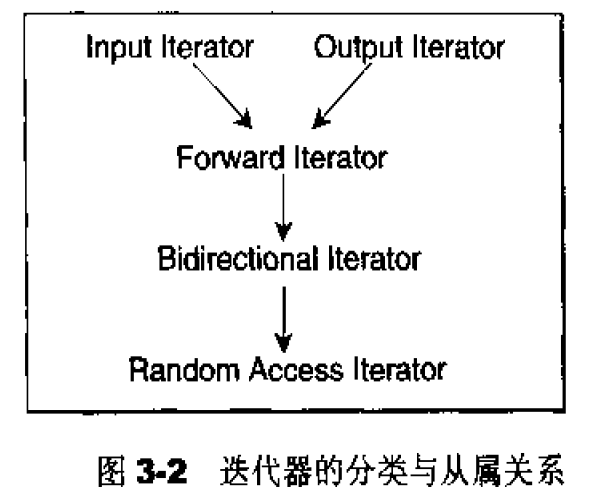
迭代器分类：

迭代器类型	功能
输入迭代器	只读
输出迭代器	只写
前向迭代器	只能向前进行读写操作
双向迭代器	两个方向均可进行读写操作
随机访问迭代器	随机访问，可读写操作，功能最全

设计适当的相应型别( associated types），是迭代器的责任。设计适当的迭代器，则是容器的责任。唯容器本身，才知道该设计出怎样的迭代器来遍力自己，并执行迭代器该有的各种行为（前进、后退、取值、取用成员…)。至于算法，完全可以独立于容器和迭代器之外自行发展，只要设计时以送代器为对外接口就行。

traits编程技法大量运用于STL实现品中。它利用“内嵌型别”的编程技巧与编译器的remplate参数推导功能，增强C++未能提供的关于型别认证方面的能力，妳补C++不为强型别( strong typed）语言的遗憾。了解traits 编程技法，就像获得“芝麻开r门1”的口诀-样，从此得以一窥STL源代码堂奥、

4. 序列式容器

容器：置物之所也
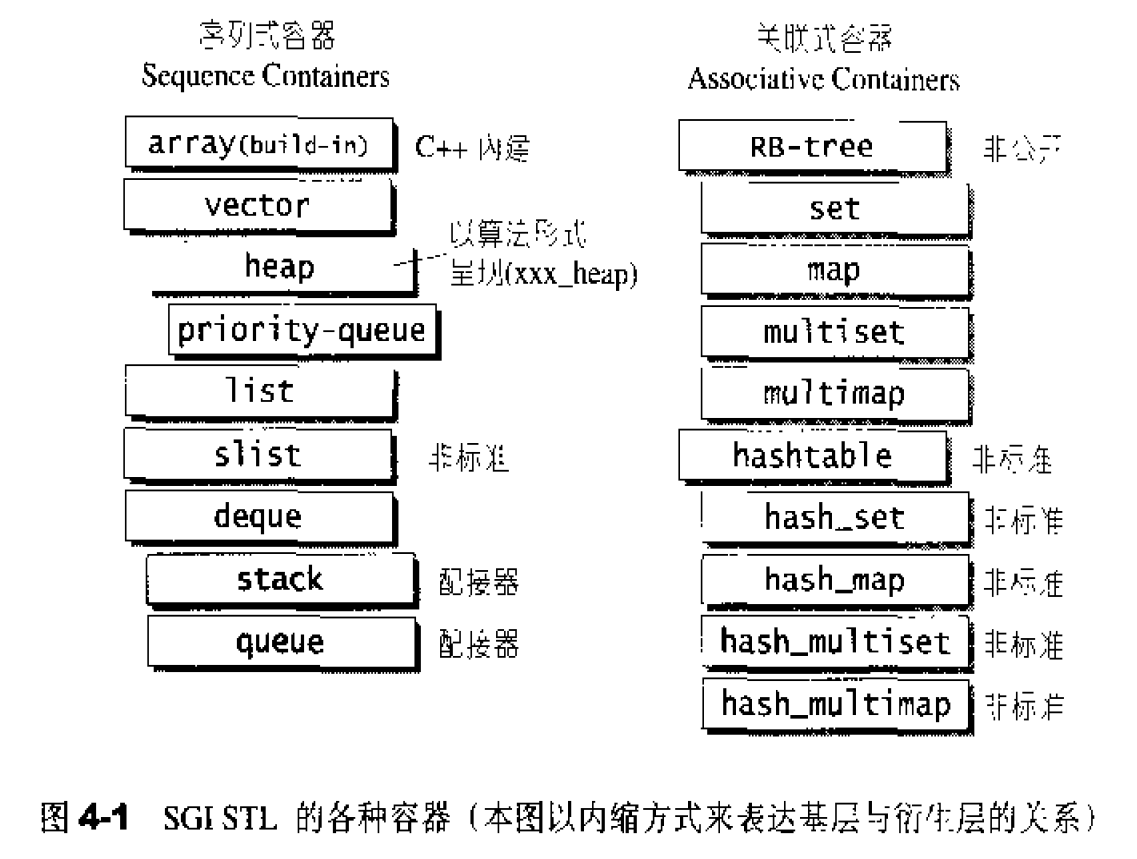
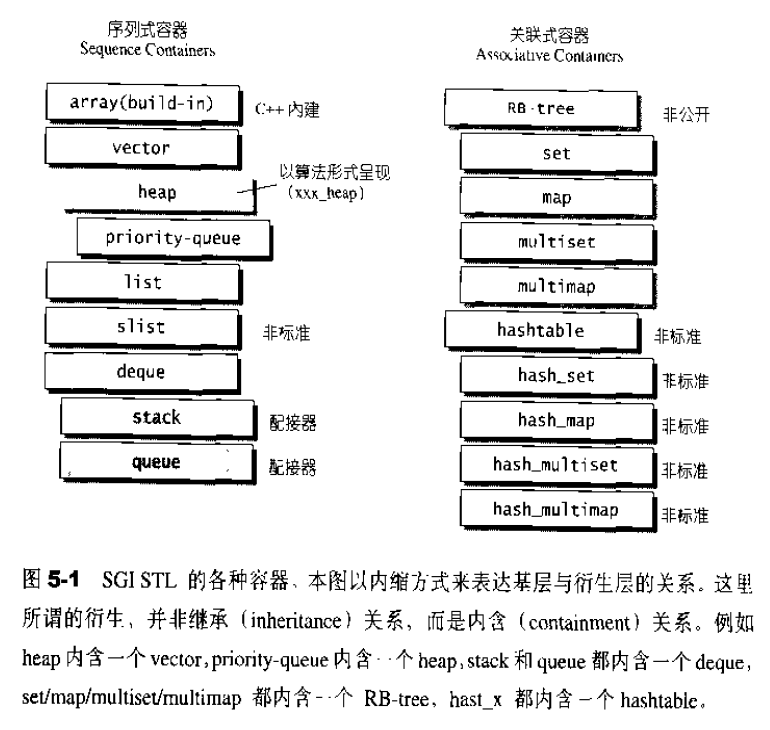
根据数据在容器中的排列特性分类：序列式容器和关联式容器。

这里所谓的衍生，并非派生 （inheritance）关系，而是内含（containment〉关系。例如heap内含一个vector，priority-queue内含一个heap、stack 和 queue都含一个deque，set/map/multisetmultimap都内含一个RB-tree，hast_x都内含一个hashtable.

序列式容器，其中的元素都可序，但未必有序。C++本身提供了array，STL另外提供了vector, list, deque, stack, queue, priority-queue等等序列容器，其中stack和queue是将deque改投换面，技术上归结为一种配接器(adapter)。

vector

vector的数据安排以及操作方式，与array非常相似。两者的唯一差别在于空间的运用的灵活性。array是静态空间，一旦配置了就不能改变，要换个大（或小)一点的房子，一切琐细得由客户端自己来：首先配置–块新空间，然后将元素从旧址——搬往新址，再把原来的空间释还给系统。vector是动态
空间，随着元素的加人，它的内部机制会自行扩充空间以容纳新元素。因此，vector的运用对于内存的合理利用与运用的灵活性有很大的帮助,我们再也不必因为害怕空间不足而一开始就要求一个大块头 array了，我们可以安心使用vector，吃多少用多少。

vector 的实现技术，关键在于其对大小的控制以及重新配置时的数据移动效率。一旦vector 1旧有空间满载，如果客户端每新增一个元素，vector内部只是扩充一个元素的空间，实为不智，因为所谓扩充空间（不论多大），一如稍早所说，是“配置新空间，数据移动，释还旧空间”的大工程，时间成本很高，应该加入某种未雨绸缪的考虑﹑稍后我们便可看到SG vector的空间配置策略。

如下将局部内容进行查看：
iterator start; // 表示目前使用空间的头
iterator end; // 表示目前使用空间的尾
iterator end_of_storage; // 表示目前可用空间的尾

iterator begin() { 
   return start;}
iterator end() { 
   return end;}
size_type size() const { 
   return size_type(end() - begin());}
size_type capacity() const { 
   return size_type(	end_of_storage - begin());}
bool empty() const { 
   return begin() == end();}
reference operator[] { 
   size_type n} { 
   return *(begin() + n);}
reference front() { 
   return *(begin());}
reference back() { 
   return *(end()-1)};

vector维护的是一个连续线性空间,所以不论其元素型别为何，普通指针都可以作为vector的迭代器而满足所有必要条件，因为vector迭代器所需要的操作行为，如operator* , operator->, 0perator++, operator–, operator+ , operator-,operator+=, operator-=，普通指针天生就具备。vector支持随机存取，而普通指针正有着这样的能力。所以，vector提供的是Random Access lterators。

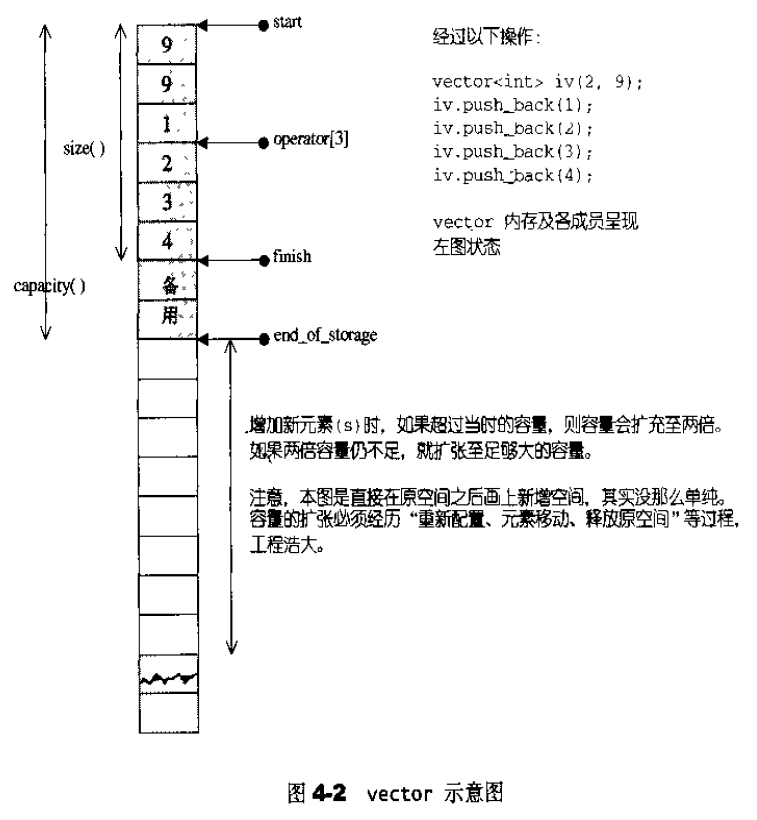
vector所采用的数据结构非常简单：线性连续空间。它以两个迭代器start和finish分别指向配置得来的连续空间中目前已被使用的范围，并以迭代器end_of_storage指向整块连续空间（含备用空间）的尾端。

为了降低空间配置时的速度成本，vector ‘实际配置的大小可能比客户端需求量更大一些，以备将来可能的扩充。这便是容量（( capacity）的观念。换句话说，–个vector的容量永远大于或等于其大小。一旦容量等于大小，便是满载，下次再有新增元素，整个vector 就得另觅居所，见图4-2。

运用start, finish,end_of_storage 三个迭代器，便可轻易地提供首尾标示、大小、容量、空容器判断、注标（[ ]）运算子、最前端元素值、最后端元素值…等机能;

vector提供许多constructors，其中一个允许我们指定空间大小及初值:

注意，所谓动态增加大小，并不是在原空间之后接续新空间（因为无法保证原空间之后尚有可供配置的空间），而是以原大小的两倍另外配置一块较大空间，然后将原内容拷贝过来，然后才开始在原内容之后构造新元素，并释放原空间。因此，对vector 的任何操作，一旦引起空问重新配置，指向原vector的所有迭代器就都失效了。这是程序员易犯的一个错误，务需小心。

问答1：puch_back()增加元素过程？

首先，判断是否满足容器大小的要求，若不满足，要进行容器扩充
其次，在end()位置处增加元素，end后移一位。

问答2：insert(pos, n, i)插入元素过程？

首先，判断是否满足容器大小的要求，若不满足，要进行容器扩充
其次，在pos位置及后面的元素进行后移n个单位，再将n个i复制到pos+n位置中。
最后，将end()位置修改end()+n;

问答3：pop_back()删除元素位置过程？

直接将end()位置前一一位即可

问答4：erase(vector, s, e)删除元素位置过程？

首先，将e位置后面的元素复制到从s位置开始到s+end()-e结束
其次，将end()位置向前移动e-s个单位

list

相较于vector的连续线性空间，list 就显得复杂许多、它的好处是每次插人或删除一个元素，就配置或释放一个元素空间。因此，list 对于空间的运用有绝对的精准，一点也不浪费。而日.，对于任何位置的元素插人或元素移除，list永远是常数时间。

list 和vector是两个最常被使用的容器。什么时机下最适合使用哪种容器，必须视元素的多寡、元素的构造复杂度（有无 non-trivial copy constructor,non-trivial copy assignmen operator)、元素存取行为的特性而定。

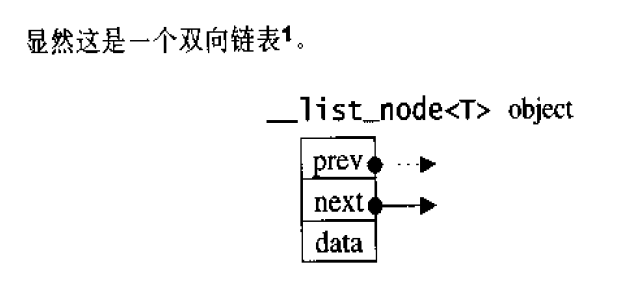
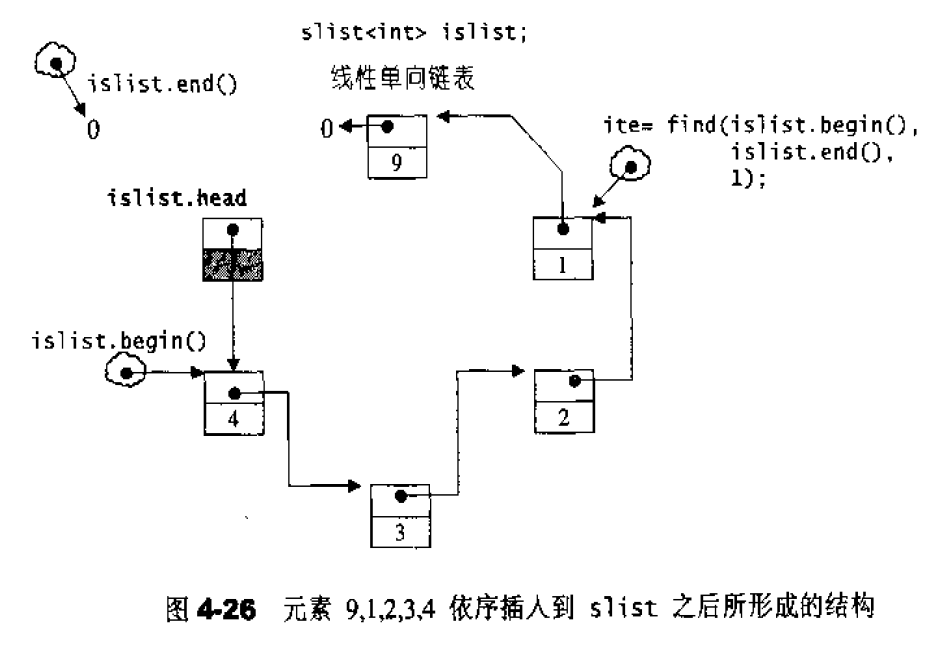
**List本质是一个环形双向链表!**只要知道它的一个指针，便可完整遍历整个链表。

template <class T>
struct __list_node { 
   
	typedef void* void_pointer;
	void_pointer prev; // 类别为void*, 其实可设为 __list_node<T>*
	void_pointer next;
	T data;
}

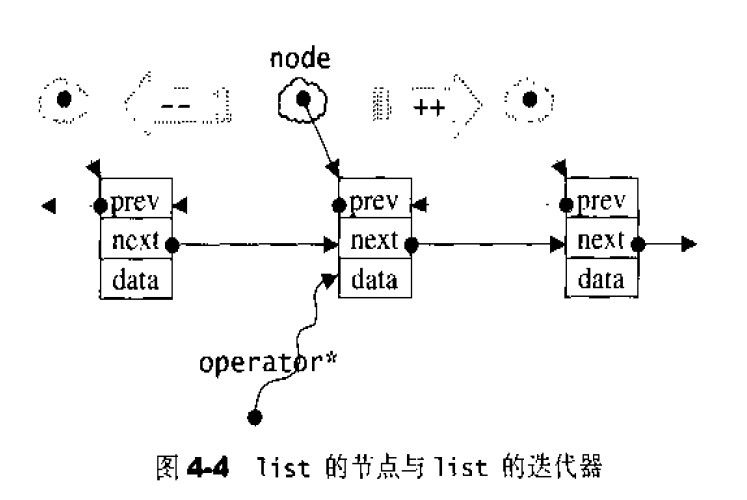
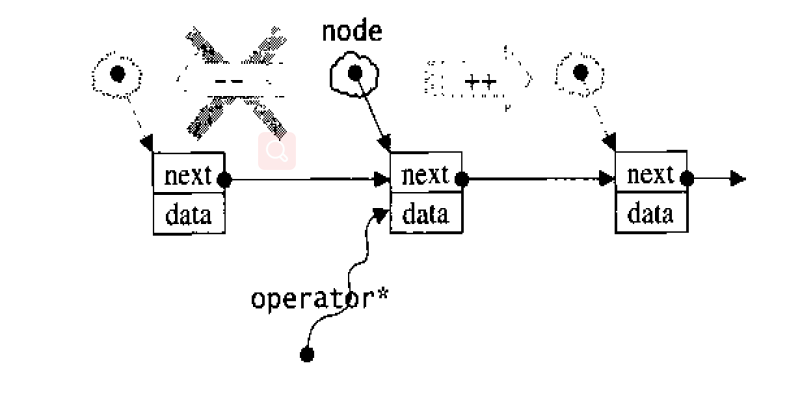
list 不再能够像vector一样以普通指针作为迭代器，因为其节点不保证在储存空间中连续存在。list迭代器必须有能力指向 list的节点，并有能力进行正确的递增、递减、取值、成员存取等操作。所谓“1ist迭代器正确的递增、递减、取值、成员取用”操作是指，递增时指向下一个节点，递减时指向上一个节点，取值时取的是节点的数据值，成员取用时取用的是节点的成员，如图4-4。

由于STLlist是一个双向链表(double linked-list)，迭代器必须具备前移、后移的能力，所以list提供的是Bidirectional iterators.

list有一个重要性质:插入操作( insert）和接合操作(splice）都不会造成原有的1ist 迭代器失效。这在vector是不成立的，因为vector的插入操作可能造成记忆体重新配置,导致原有的迭代器全部失效.甚至list的元素删除操作( erase )，也只有“指向被删除元素”的那个送代器失效，其它选代器不受任何影响.

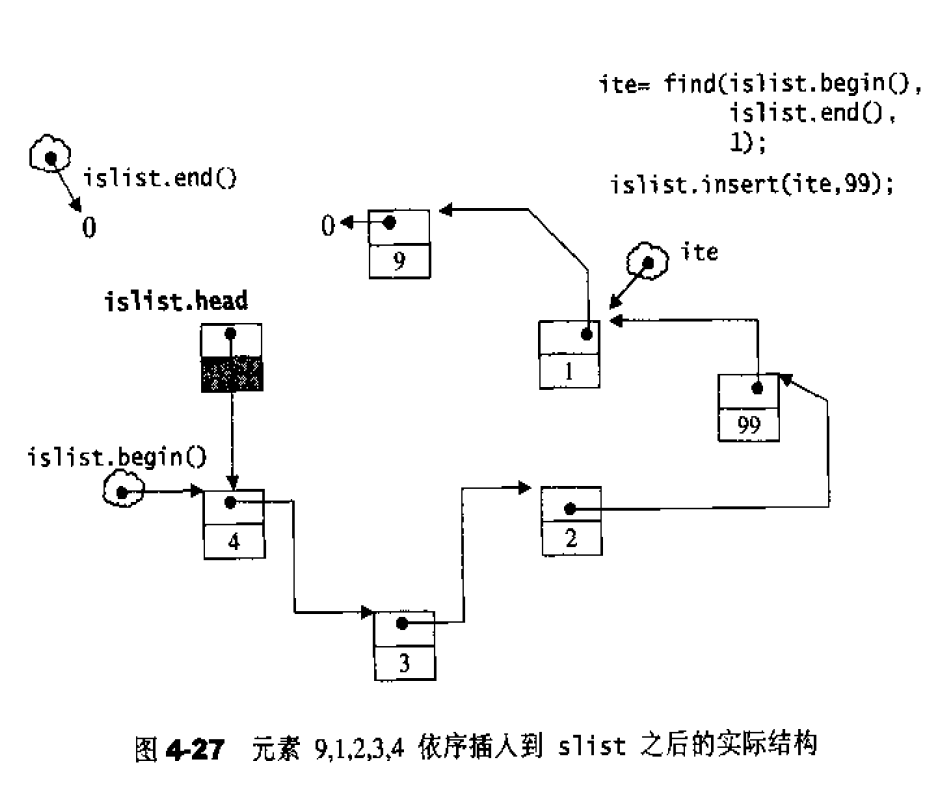
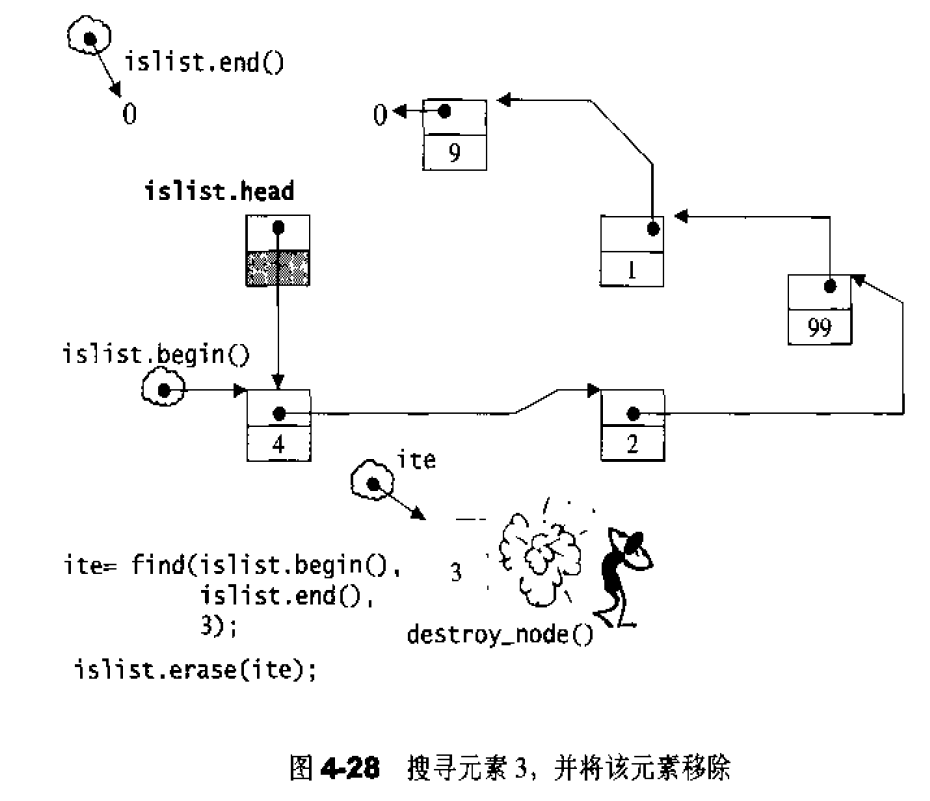
注：list也有一个单向链表slist

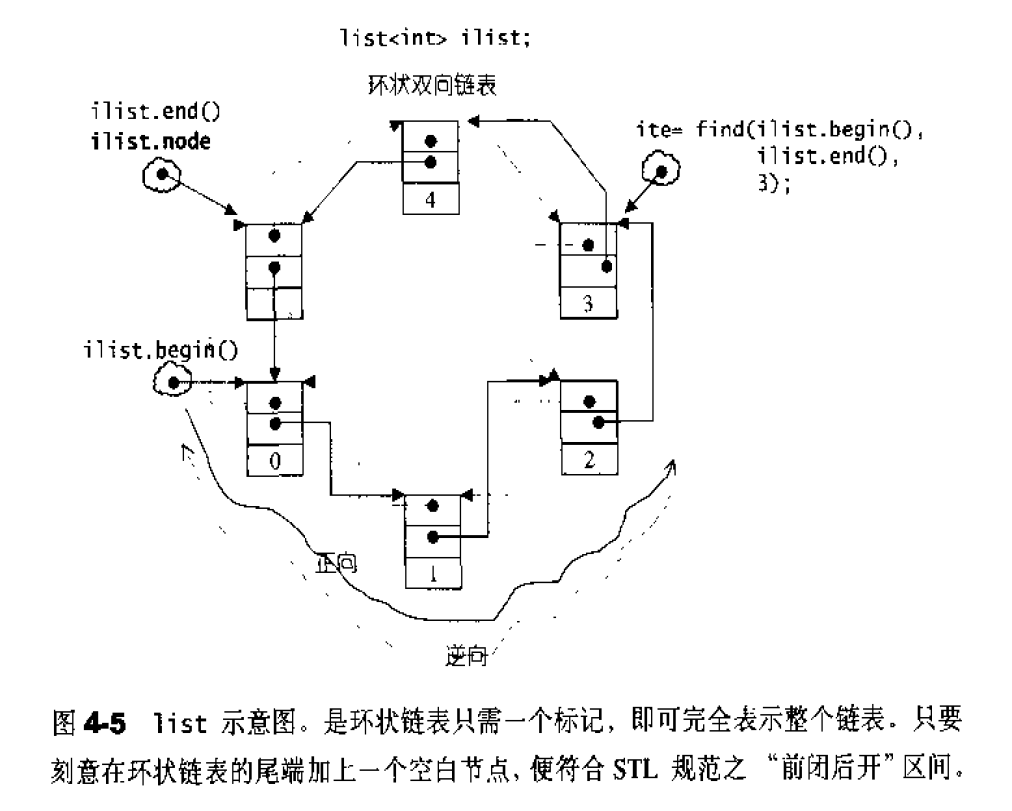
如果让指针node 指向刻意置于尾端的一个空白节点，node便能符合STL对于“前闭后开”区间的要求，成为last迭代器，如图4-5所示。这么一来，以下几个函数便都可以轻易完成:

所谓的空白结点可以理解为增加一个头结点，辅助整个链表。

过程演示使用链表，便于理解，实际是通过iterator进行遍历循环的，(*it.node).next / (*it.node).prev即可

问题1：添加第一个元素过程？

node->next = newnode;node->pre = newnode;
newnode->prev=node;newnode->next=node;

问题2：insert(pos, val)过程？假设当前结点node

newnode->next = node; newnode->prev = node->prev;
node->prev->next = newnode; node->prev = newnode;

问题3：erase(pos)过程？假设当前结点node

ListNode* deleteNode = node;
node->prev->next = newnode; node->next->prev = newnode;
delete deleteNode;

问题4：判断链表是否为空？

return node->next == node;

问题5：删除全部链表

ListNode* cur = node->next; //首节点
while (cur != node){

ListNode* tmp = cur;
cur->prev->next = cur->next;
cur->next->prev = cur->prev;
cur = cur->next;
delete tmp;
}

问题6：迁移训练：将first到last元素放入pos位置中
first.”>

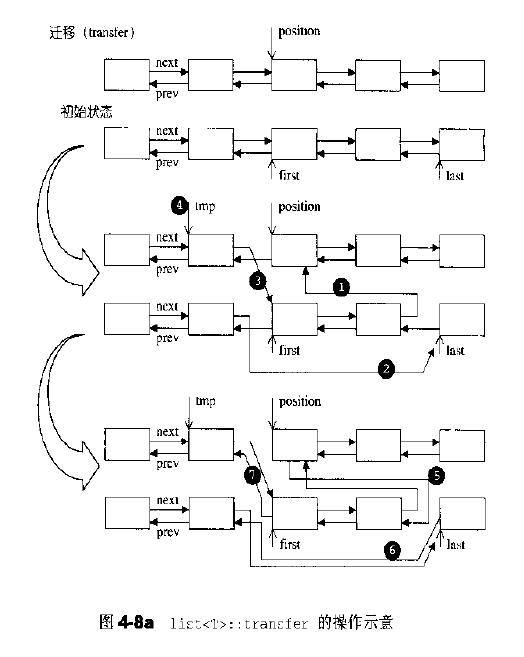
deque

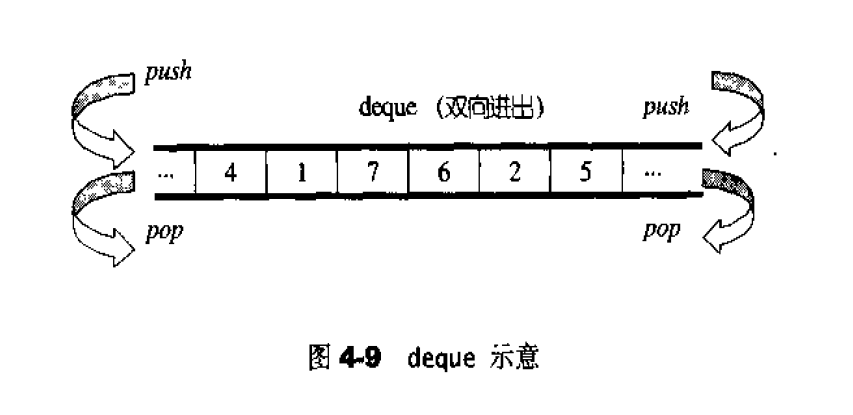
vector是单向开口的连续线性空间, deque 则是一种双向开口的连续线性空间。所谓双向开口，意思是可以在头尾两端分别做元素的插人和删除操作，如图4-9所示。vector当然也可以在头尾两端进行操作（从技术观点），但是其头部操作效率奇差，无法被接受。

deque和vector的最大差异，一在于deque 允许于常数时间内对起头端进行元素的插入或移除操作，二在于deque没有所谓容量(capacity）观念，因为它是动态地以分段连续空间组合而成，随时可以增加一段新的空间并链接起来。换句话说，像vector那样“因旧空间不足而重新配置一块更大空间，然后复制元素，再释放旧空间”这样的事情在deque是不会发生的。也因此，deque没有必要提供所谓的空间保留（reserve）功能。

虽然deque也提供Ramdon Acces lterator，但它的迭代器并不是普通指针,其复杂度和vector 不可以道里计〔稍后看到源代码，你便知道），这当然影响了各个运算层面。因此，除非必要，我们应尽可能选择使用vector而非deque。对deque进行的排序操作,为了最高效率,可将deque 先完整复制到一个vector身上，将 vector排序后（利用STL sort算法），再复制回deque.

deque中控器：

deque是连续空间（至少逻辑上看来如此），连续线性空间总令我们联想到array 或vector. array无法成长，vector虽可成长，却只能向尾端成长，而且其所谓成长原是个假象，事实上是(1〕另觅更大空间:(2〉将原数据复制过去;(3)释放原空间三部曲。如果不是vector每次配置新空间时都有留下一些余裕，其“成长”假象所带来的代价将是相当高昂.

deque系由一段一段的定量连续空间构成。一旦有必要在 deque的前端或尾端增加新空间，便配置一段定量连续空间，串接在整个deque的头端或尾端。deque的最大任务，便是在这些分段的定量连续空间上，维护其整体连续的假象，并提供随机存取的接口。避开了“重新配置、复制、释放”的轮回，代价则是复杂的迭代器架构。

受到分段连续线性空间的字面影响，我们可能以为deque的实现复杂度和vector 相比虽不中亦不远矣，其实不然。主要因为，既日分段连续线性空间，就必须有中央控制，而为了维持整体连续的假象，数据结构的设计及迭代器前进后退等操作都颇为繁琐。deque 的实现代码分量远比 vector或list都多得多、

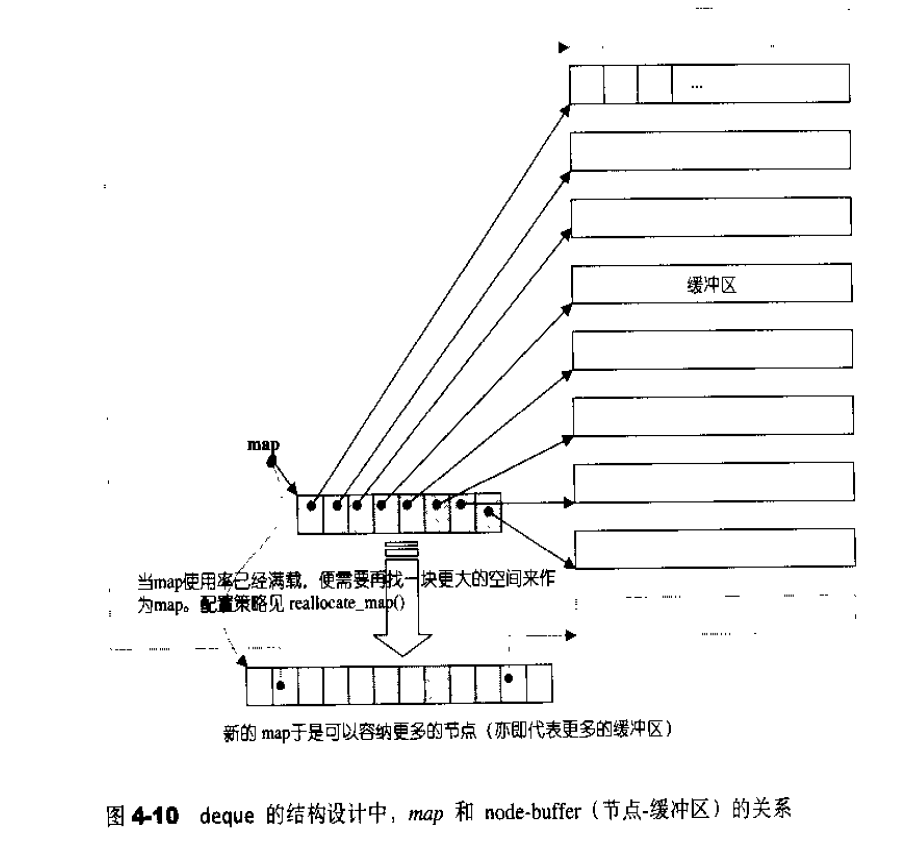
deque 采用一块所谓的map(注意，不是STL的map容器）作为主控。这里所谓map是一小块连续空间，其中每个元素（此处称为一个节点，node）都是指针，指向另一段（较大的）连续线性空间，称为缓冲区。缓冲区才是deque 的储存空间主体。SGI STL允许我们指定缓冲区大小，默认值0表示将使用512bytes缓冲区。

deque内部工作原理:

deque内部有个中控器，维护每段缓冲区中的内容，缓冲区中存放真实数据

中控器维护的是每个缓冲区的地址，使得使用deque时像一片连续的内存空间

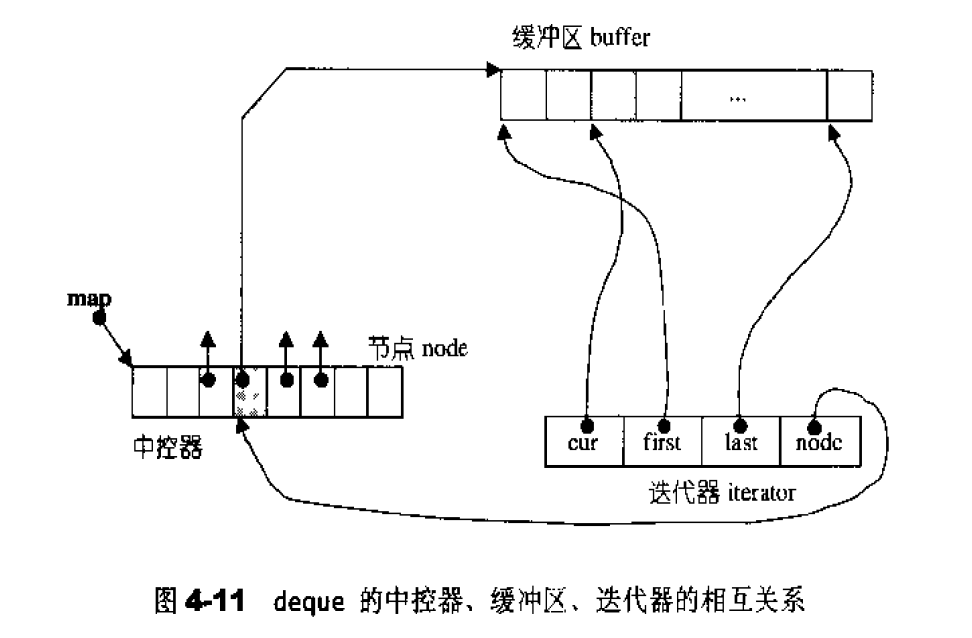
迭代器：
deque是分段连续空间。维持其“整体连续”假象的任务，落在了迭代器的operator++和operator–两个运算子身上


下面是deque迭代器的几个关键行为。由于迭代器内对各种指针运算都进行了重载操作，所以各种指针运算如加、减、前进、后退都不能直观视之。其中最关键的就是:一旦行进时遇到缓冲区边缘，要特别当心，视前进或后退而定，可能需要调用set_node i )跳一个缓冲区。

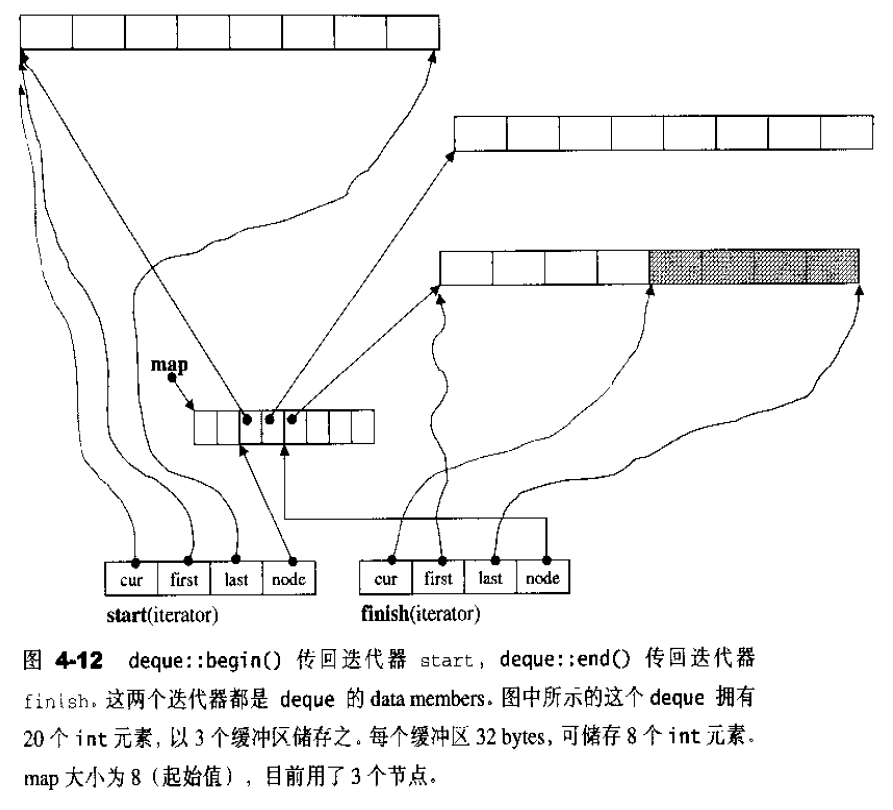
deque 除了维护一个先前说过的指向map 的指针外,也维护start , finish两个迭代器，分别指向第一缓冲区的第一个元素和最后缓冲区的最后一个元素（的下一位置)。此外，它当然也必须记住目前的map大小。因为一旦map所提供的节点不足，就必须重新配置更大的一块 map。

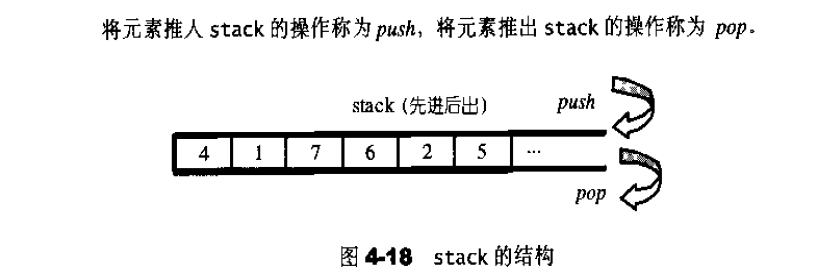
stack

stack 是·种先进后出（First In Last Out，FILO〉的数据结构。它只有一个出口，形式如图4-18所示。stack 允许新增元素、移除元素、取得最顶端丘素。但除了最顶端外，没有任何其它方法可以存取stack 的其它元素，换言之，stack不允许有遍历行为。

以某种既有容器作为底部结构,将其接口改变，使之符合“先进后出”的特性,形成一个stack,是很容易做到的.deque是双向开口的数据结构,若以deque为底部结构并封闭其头端开口，便轻而易举地形成了一个stack。因此，SGI STL便以 deque作为缺省情况下的 stack 底部结构，stack的实现因而非常简单，源代码十分简短，本处完整列出。

由于stack 系以底部容器完成其所有工作，而具有这种“修改某物接口，形成另一种风貌”之性质者，称为adapter（配接器)，因此，STL stack 往往不被归类为container〈容器），而被归类为container adapter.

stack 所有元素的过出都必须符合“先进后出”的条件，只有stack顶端的元素，才有机会被外界取用。 stack 不提供走访功能，也不提供迭代器。

list作为stack的底层容器

queue

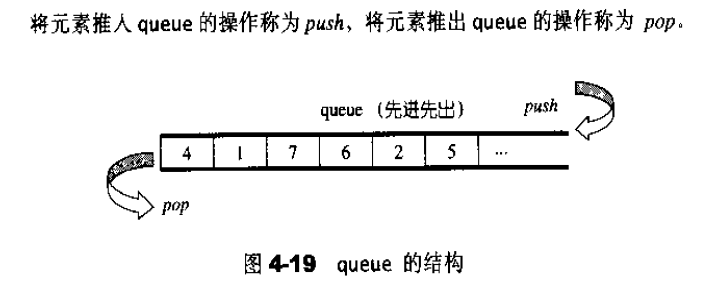
queue是一种先进先出(（First In First Out，FIFO)的数据结构。它有两个出口，形式如图4-19所示。queue 允许新增元素、移除元素、从最底端加入元素、取得最顶端元素。但除了最底端可以加入、最顶端可以取出外，没有任何其它方法可以存取queue的其它元素。换言之，queue不允许有遍历行为。

以某种既有容器为底部结构，将其接口改变，使其符合“先进先出”的特性，形成一个queue,是很容易做到的.deque 是双向开口的数据结构,若以 deque 为底部结构并封闭其底端的出口和前端的人口，便轻而易举地形成了一个queue。因此，SGI STL便以deque 作为缺省情况下的queue底部结构，queue 的实现因而非常简单，源代码十分简短，本处完整列出。

由于queue系以底部容器完成其所有工作、而具有这种“修改某物接П，形成另一种风貌”之性质者，称为adapter(配接器），因此，STL queue往往不被归类为container （容器），而被归类为container adapter。

queue所有元素的进出都必须符合“先进先出”的条件，只有queue 顶端的元素，才有机会被外界取用.queue不提供遍历功能，也不提供迭代器。

除了deque 之外，list也是双向开口的数据结构。上述queue源代码中使用的底层容器的函数有empty. size，back,push_back，pop_back，凡此种种，list 都具备。因此，若以list为底部结构并封闭其头端开口，一样能够轻易形成一个queue。

heap

heap并不归属于STL容器组件，它是个幕后英雄，扮演priority queue的助手。顾名思义，priority queue 允许用户以任何次序将任何元素推人容器内,但取出时一定是从优先权最高(也就是数值最高)的元素开始取.binarymax heap正是具有这样的特性，适合作为priority queue的底层机制。

让我们做一点分析。如果使用list作为priority queue 的底层机制，元素插入操作可享常数时间。但是要找到list中的极值，却需要对整个list进行线性扫描。我们也可以改变做法，让元素插入前先经过排序这一关，使得list的元素值总是由小到大（或由大到小〕，但这么一来，收之东隅却失之桑榆:虽然取得极值以及元素删除操作达到最高效率，可元素的插人却只有线性表现。

比较麻辣的做法是以binary search tree(如5.1节的RB-tree)作为 priorityqueue 的底层机制。这么一来，元素的插入和极值的取得就有O(iogN的表现.但杀鸡用牛刀，未免小题大做，一来 binary search tree的输入需要足够的随机性，二来 binary search tree 并不容易实现.priority queue 的复杂度，最好介于queue和 binary search tree 之间，才算适得其所。binary heap便是这种条件下的适当候选人。

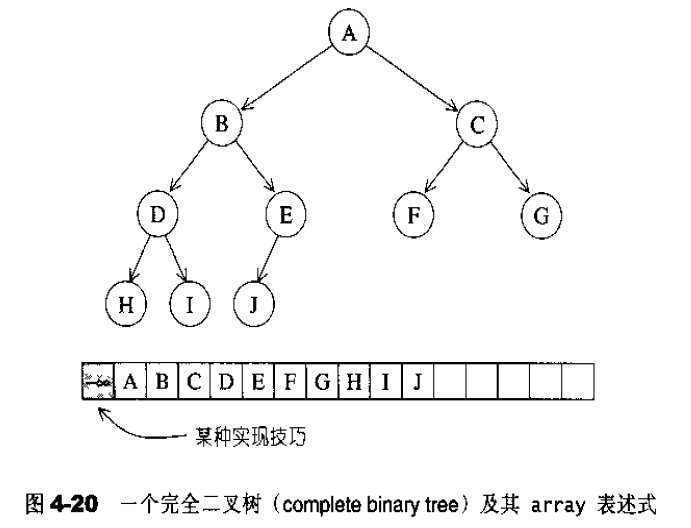
所谓binary heap 就是一种complete binary tree (完全二叉树)2、也就是说，整棵binary tree除了最底层的叶节点(s之外，是填满的，而最底层的叶节点(s)由左至右又不得有空隙。图4-20所示的是一个complete binary tree.

complete binary tree 整棵树内没有任何节点漏洞，这带来一个极大的好处:我们可以利用array来储存所有节点。假设动用–个小技巧3，将array的0元素保留（或设为无限大值或无限小值），那么当complete binary tree中的某个节点位于array 的i 处时，其左子节点必位于array的21处，其右子节点必位于array 的2i+1处，其父节点必位于“i/2”处(此处的“”权且代表高斯符号，取其整数）。通过这么简单的位置规则，array 可以轻易实现出 complete binary tree。这种以array 表述tree 的方式，我们称为隐式表述法(implicit ropresentation) .

根据元素排列方式，heap可分为max-heap和 min-heap两种，前者每个节点的键值(key)都大于或等于其子节点键值，后者的每个节点键值（key〉都小于或等于其子节点键值。因此,max-heap的最大值在根节点,并总是位于底层array或vector的起头处: nin-heap 的最小值在根节点，亦总是位于底层 array或vector 的起头处。STL供应的是max-heap，因此，以下我说heap 时，指的是max-heap.

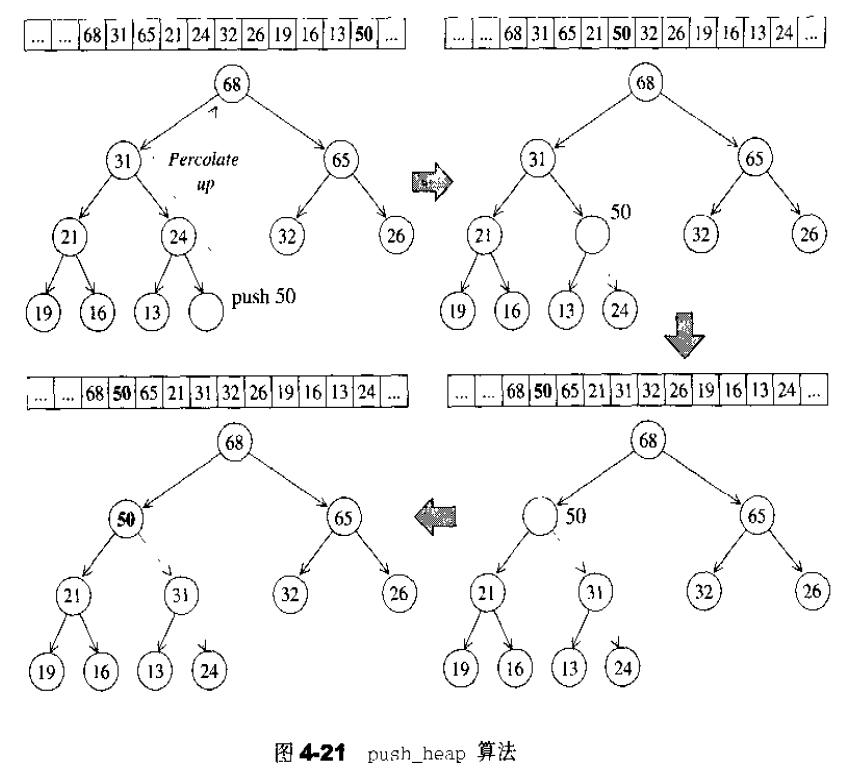
push_heap算法
图4-21所示的是push_heap 算法的实际操演情况。为了满足complete binarytree 的条件，新加入的元素一定要放在最下一层作为时节点，并填补在由左至右的第–个空格，也就是把新元素插入在底层vector 的end()处

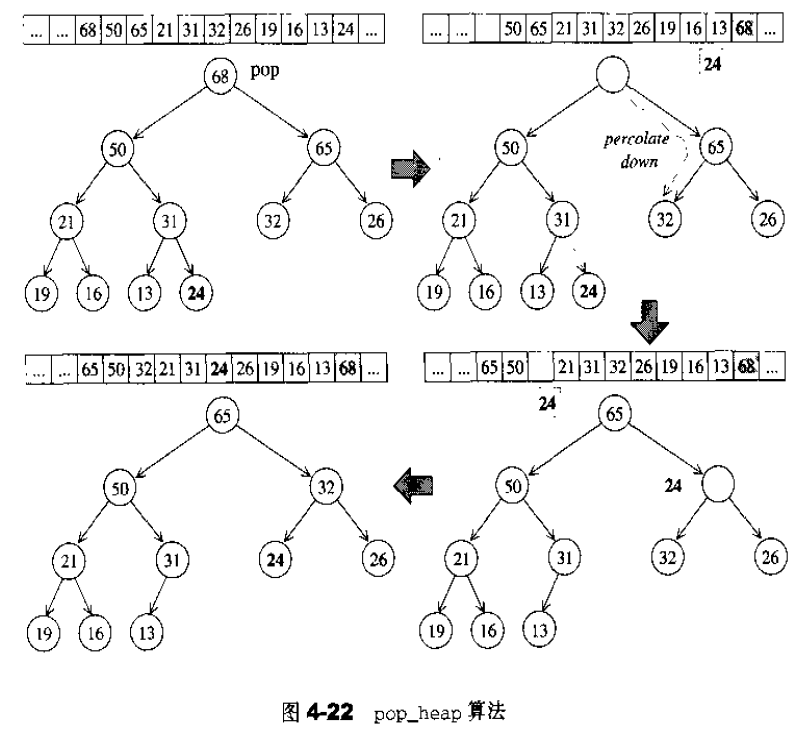
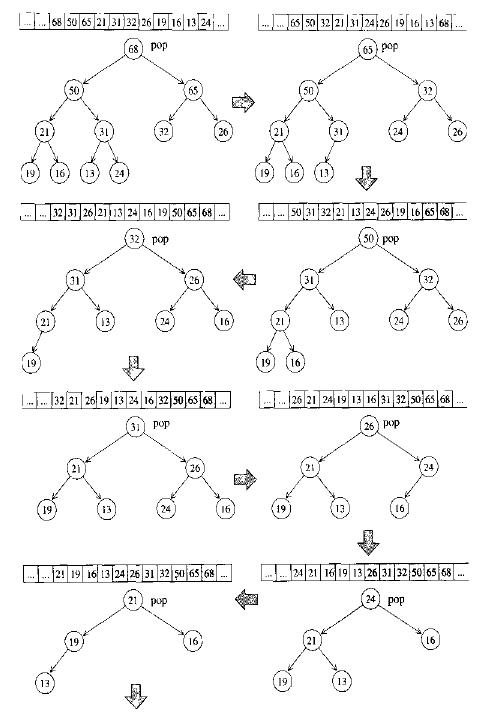
pop_head过程：将根节点与最后一个叶子结点交换，并将size-1,然后将进而进行最大根排序。
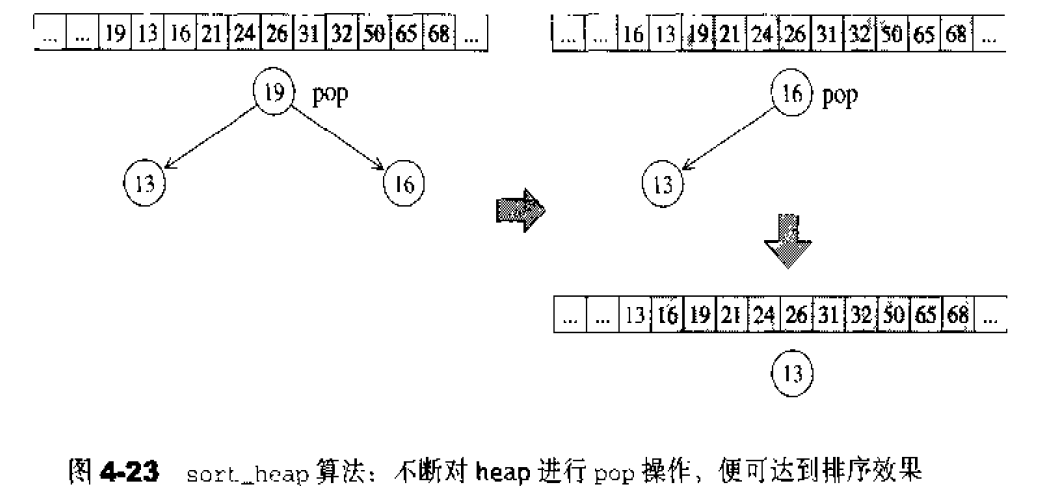
sort_heap算法过程：将pop_heap过程执行一遍即可，但不改变size大小。


heap的所有元素都必须遵循特别的(complete binary tree）排列规则，所以heap不提供遍历功能，也不提供迭代器。

priority_queue

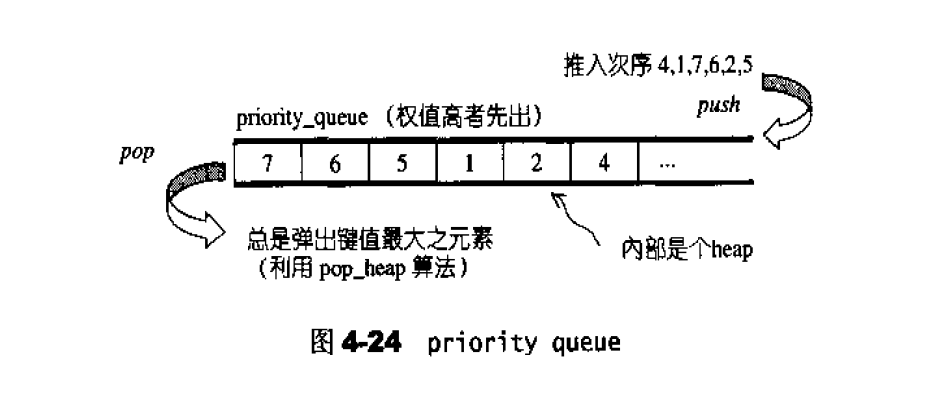
顾名思义，priority_queue是一个拥有权值观念的queue，它允许加入新元索、移除旧元索、审视元素值等功能。由于这是一个queue，所以只允许在底端加人元素，并从顶端取出元素，除此之外别无其它存取元素的途径。

缺省情况下priority_queue系利用一个max-heap 元成，后有Eq员vector表现的complete binary tree . max-heap可以满足priority_queue所需要的“依权值高低自动递增排序”的特性。

由于priority_queue完全以底部容器为根据，再加上 heap处理规则，所以其实现非常简单。缺省情况下是以vector为底部容器。

queue 以底部容器完成其所有工作。具有这种“修改某物接口，形成另一种风貌”之性质者，称为adapter（配接器)，因此，STL priority_queue往往不被归类为container(容器)﹐而被归类为container adapter.

slist

slist单向链表

5. 关联式容器

标准的STL关联式容器分为set（集合）和map（映射表）两大类，以及这两大类的衍生体multiset(多键集合）和multimap（多键映射表）。这些容器的底层机制均以RB-tree(红黑树）完成。RB-tree也是一个独立容器，但并不开放给外界使用.

所谓关联式容器，观念上类似关联式数据库（实际上则简单许多）∶每笔数据(每个元素）都有一个键值（ key)和个实值（ value )2。当元素被插人到关联式容器中时、容器内部结构（可能是RB-tree，也可能是 hash-table）便依照其键值大小,以某种特定规则将这个元素放置于适当位置.关联式容器没有所谓头尾(只有最大元素和最小元素），所以不会有所谓push_back ( ) 、 push_front ( ) 、pop_back ( )、pop_front() ; . begin ( ) .end() 这样的操作行为。

―般而言,关联式容器的内部结构是一个balanced binary tree(平衡二叉树)，以便获得良好的搜寻效率。balanced binary tree有许多种类型，包括 AVL-tree、RB-tree、AA-tree，其中最被广泛运用于STL的是RB-tree （红黑树）。

树

树(tree)，在计算机科学里，是一种十分基础的数据结构。几乎所有操作系统都将文件存放在树状结构里;几乎所有的编译器都需要实现一个表达式树(expression tree)﹔文件压缩所用的哈夫曼算法（Huffman’s Algorithm）需要用到树状结构;数据库所使用的B-tree 则是一种相当复杂的树状结构。

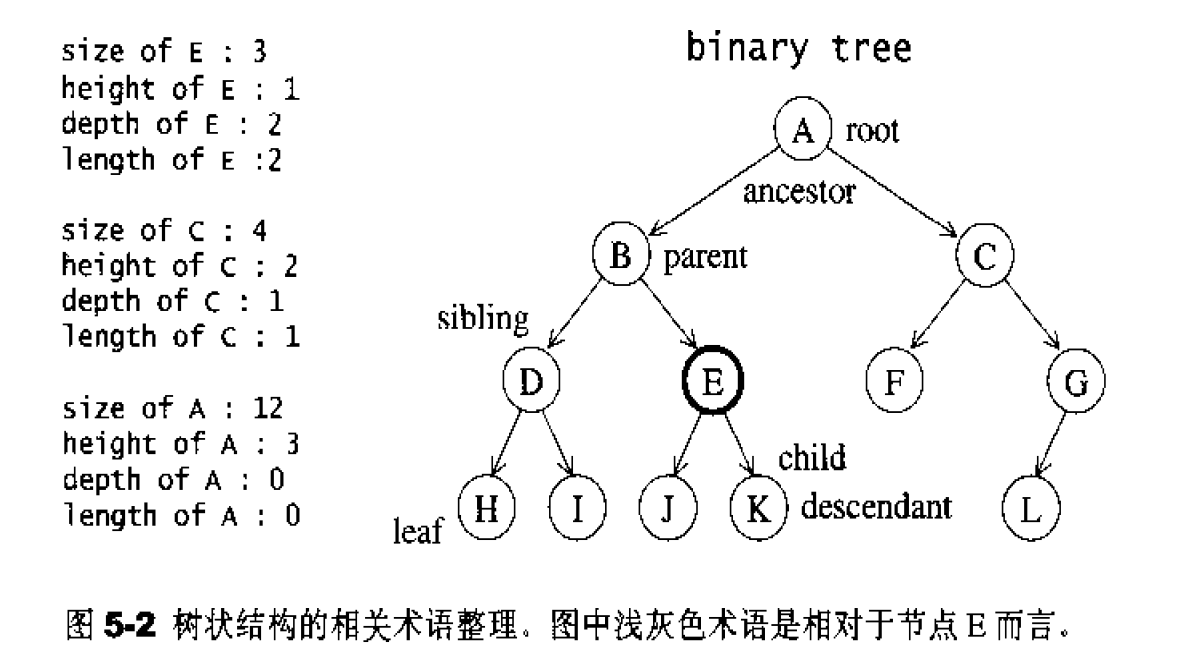
树由节点(nodes〉和边(edges）构成，如图5-2所示。整棵树有一个最上端节点，称为根节点(root)。每个节点可以拥有具方向性的边(directed edges ) ,用来和其它节点相连。相连节点之中，在上者称为父节点（ parent)，在下者称为子节点 (child).无子节点者称为叶节点（ leaf)。子节点可以存在多个，如果最多只允许两个子节点，即所谓二叉树( binary tree)。不同的节点如果拥有相同的父节点,则彼此互为兄弟节点( siblings） .根节点至任何节点之间有唯一路径( path) ,路径所经过的边数，称为路径长度（ length)。根节点至任一节点的路径长度，即所谓该节点的深度( depth)。根节点的深度永远是0。某节点至其最深子节点（叶节点）的路径长度，称为该节点的高度（height)。整棵树的高度，便以根节点的高度来代表。节点A→B之间如果存在（唯一）一条路径，那么A称为B的祖代( ancestor)，B称为A的子代 ( descendant).任何节点的大小( size）是指其所有子代（包括自己）的节点总数。

二叉搜索树

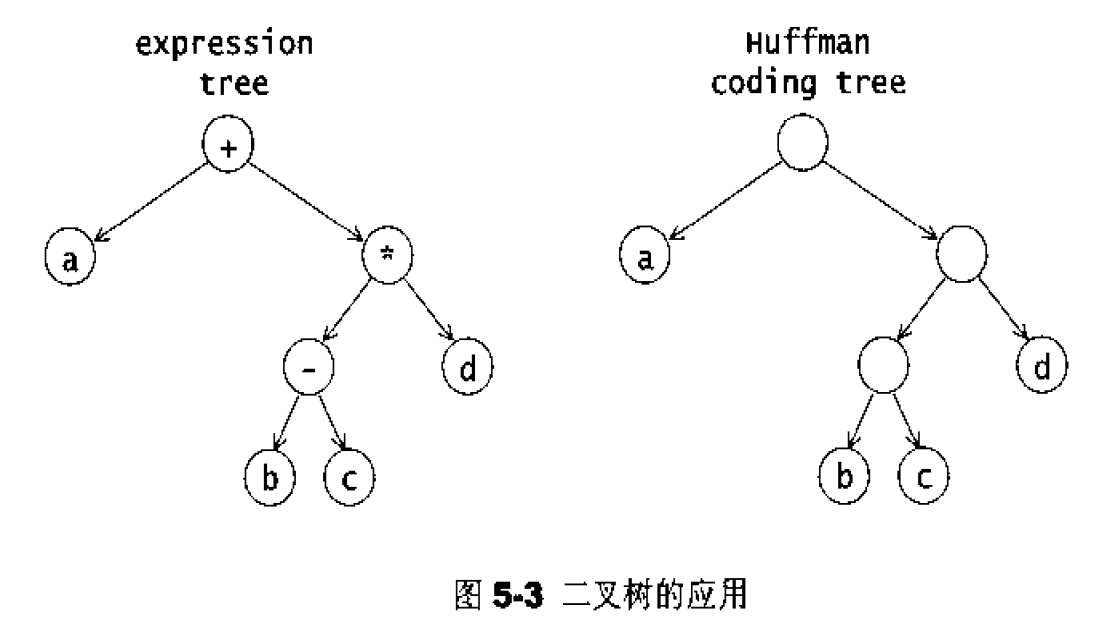
所谓二叉树( binary tree)，其意义是:“任何节点最多只允许两个子节点”。这两个子节点称为左子节点和右子节点。如果以递归方式来定义二叉树，我们可以说:“一个二叉树如果不为空，便是由一个根节点和左右两子树构成;左右子树都可能为空”。二叉树的运用极广，先前提到的编译器表达式树( expression tree)和哈夫曼编码树(Huffman coding tree）都是二叉树，如图5-3所示

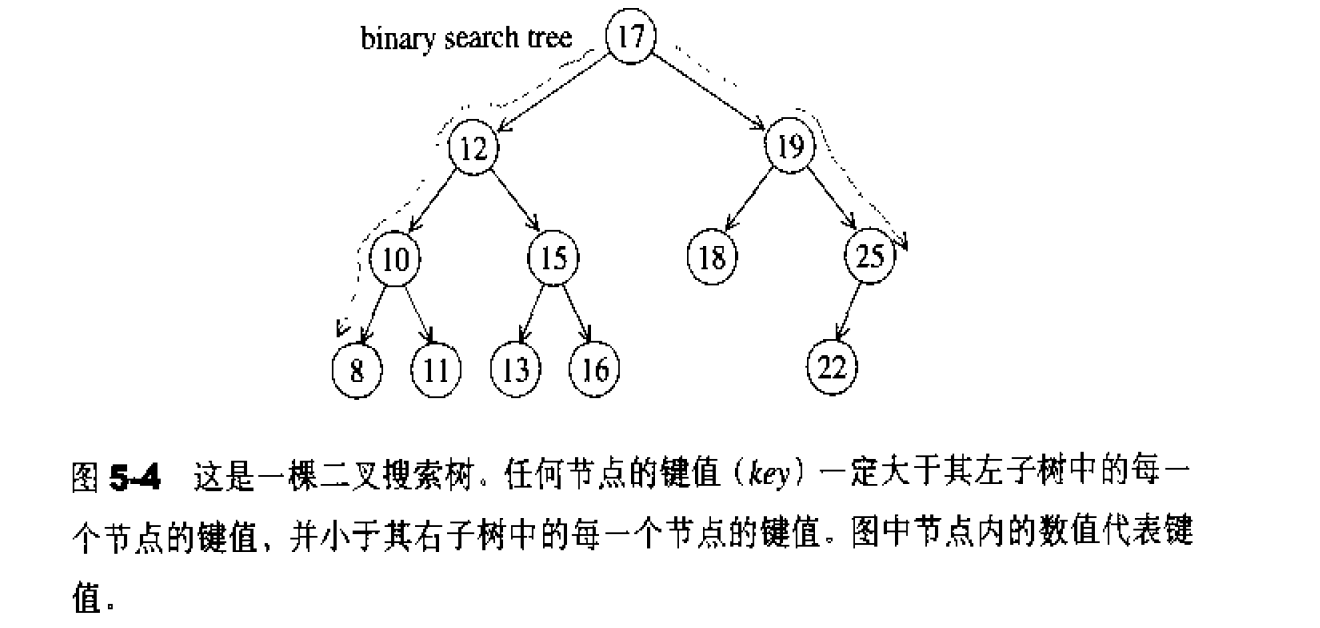
所谓二叉搜索树( binary search tree)，可提供对数时间( logarithrnic time）的元素插入和访问。二叉搜索树的节点放置规则是：任何节点的键值一定大于其左子树中的每一个节点的键值，并小于其右子树中的每一个节点的键值。因此、从根节点直往左走，直至无左路可走，即得最小元素；从根节点‘直往右走，直至无右路可走，即得最大元素。图5-4所示的就是一棵二叉搜索树。

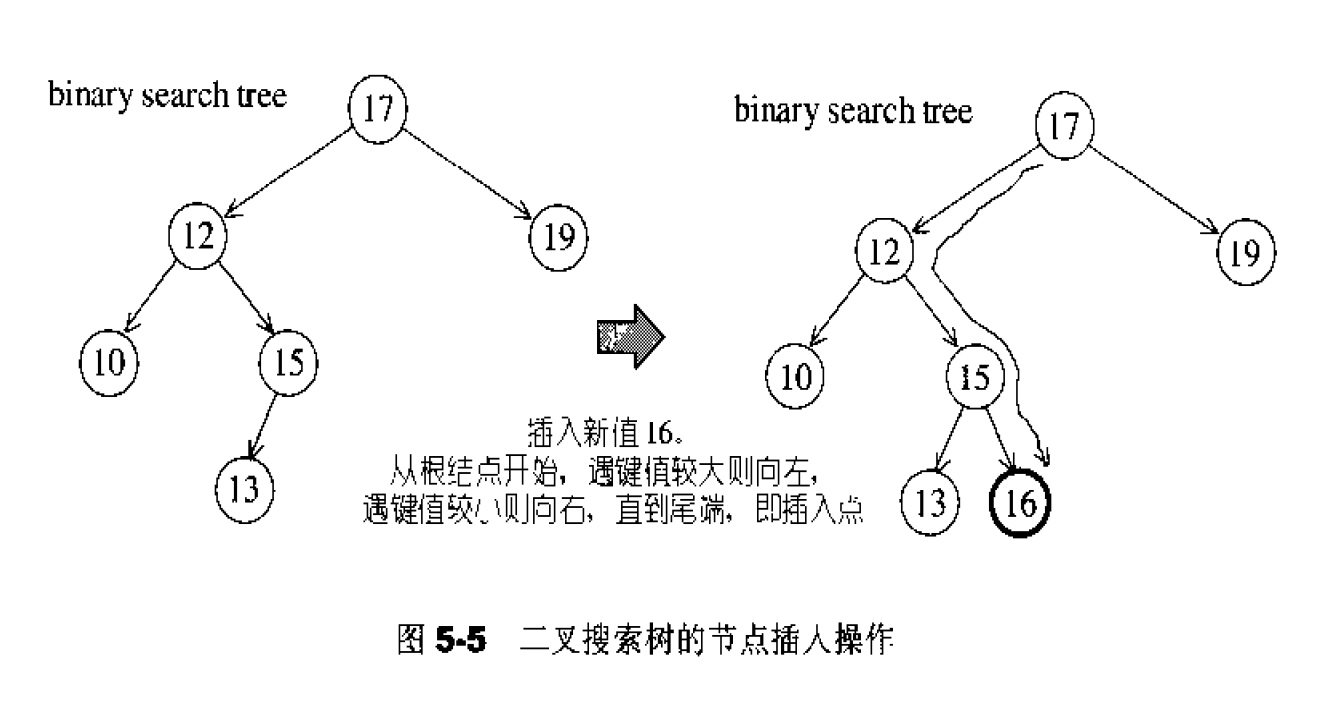
要在一棵二叉搜索树中找出最大元素或最小元素，是–件极简单的事:就像上述所言，一直往左走或-直往右走即是。比较麻烦的是元素的插入和移除。图5-5是二叉搜索树的元素插入操作图解。插人新元素时，可从根节点开始，遇键值较大者就向左，遇键值较小者就向右，一直到尾端，即为插入点。

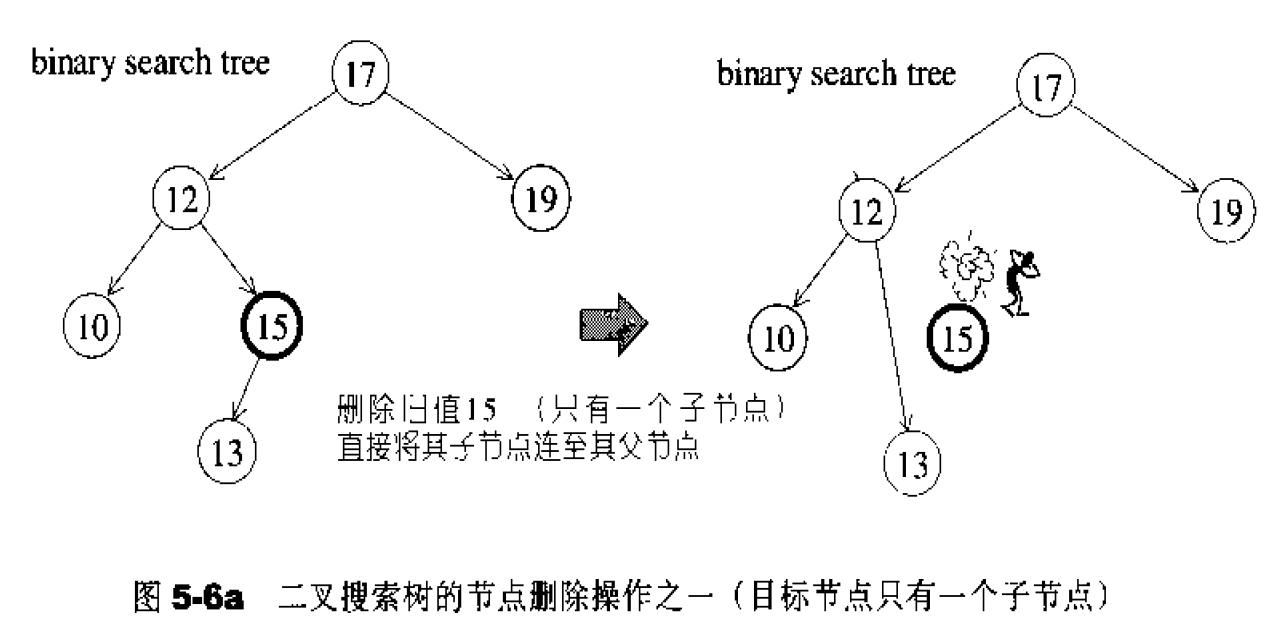
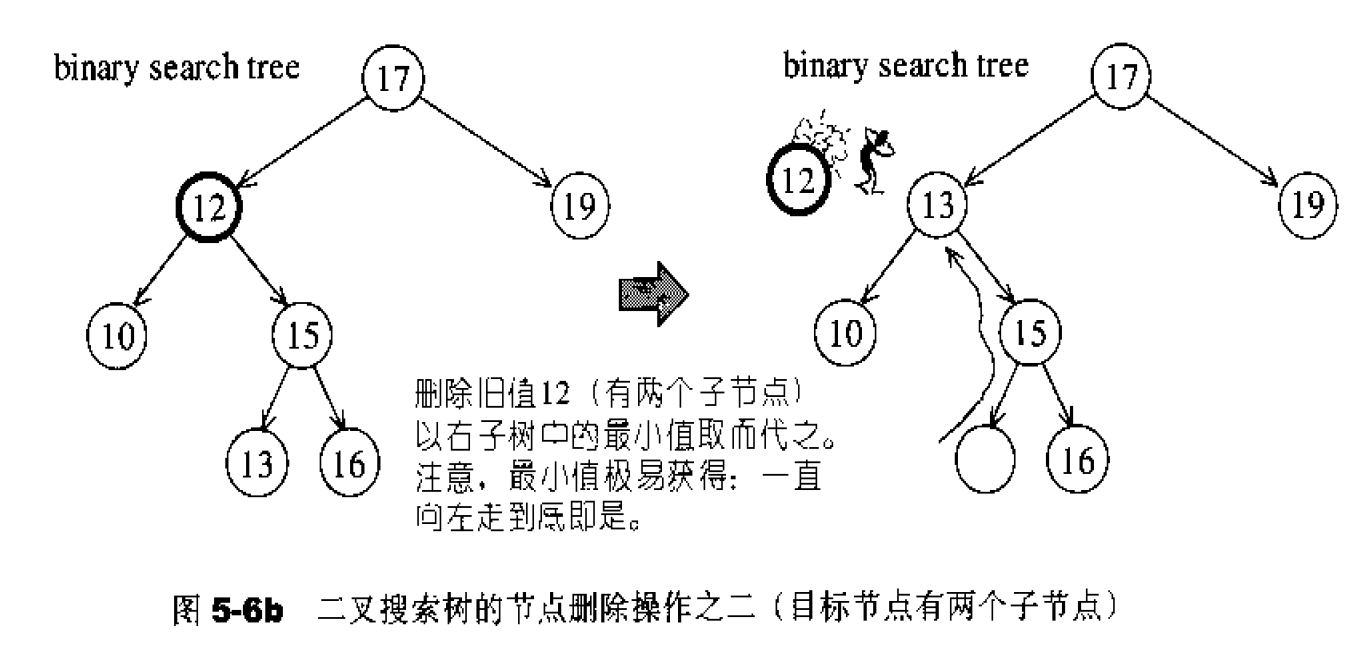
图5-6是二叉搜索树的元素移除操作图解。欲删除旧节点A，情况可分两种.如果A只有个子节点，我们就直接将A的子节点连至A的父节点，并将A删除。如果A有两个子节点，我们就以右子树内的最小节点取代A。注意，右子树的最小节点极易获得:从右子节点开始（视为右子树的根节点〉，一直向左走至底即是。

平衡二叉搜索树（balanced binary search tree）

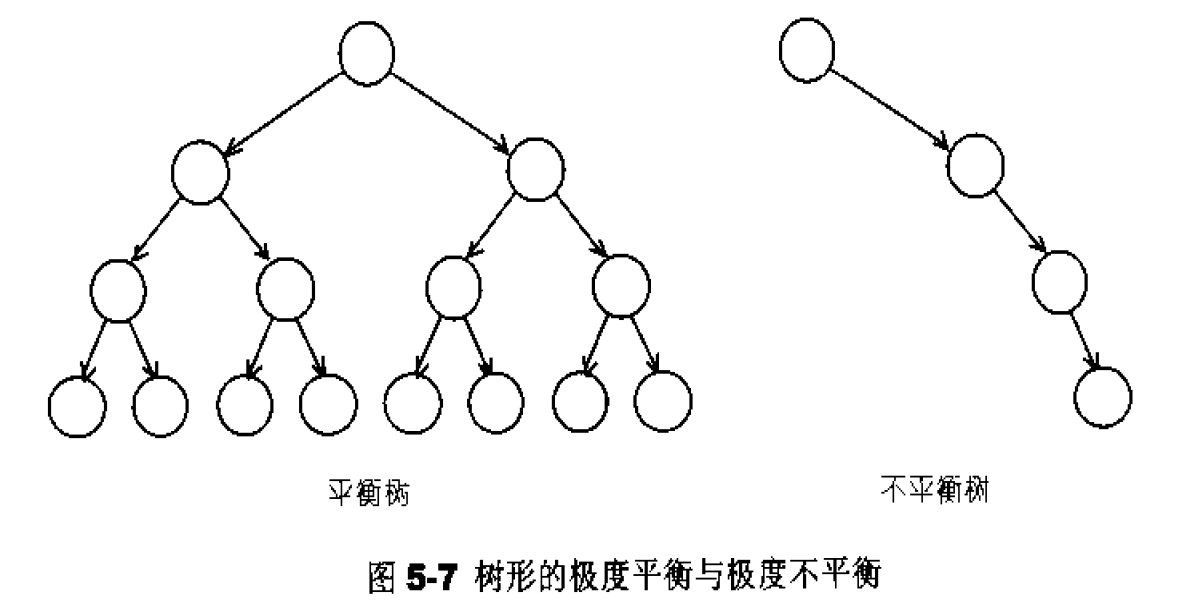
也许因为输人值不够随机，也许因为经过某些插人或删除操作，二叉搜索树可能会失去平衡，造成搜寻效率低落的情况、如图5-7所示。

所谓树形平衡与否，并没有一个绝对的测量标准。“平衡”的大致意义是:没有任何一个节点过深（深度过大)。不同的平衡条件，造就出不同的效率表现，以及不同的实现复杂度。有数种特殊结构如AVL-tree. RB-tree、AA-tree，均可实现出平衡二叉搜索树，它们都比一般的（无法绝对维持平衡的）二叉搜索树复杂，因此，插人节点和删除节点的平均时间也比较长，但是它们可以避免极难应付的最坏〔高度不平衡）情况，而且由于它们总是保持某种程度的平衡，所以元素的访问(搜寻）时间平均而言也就比较少。一般而言其搜寻时间可节省25%左右。

AVL tree (Adelson-Velskii-Landis tree)

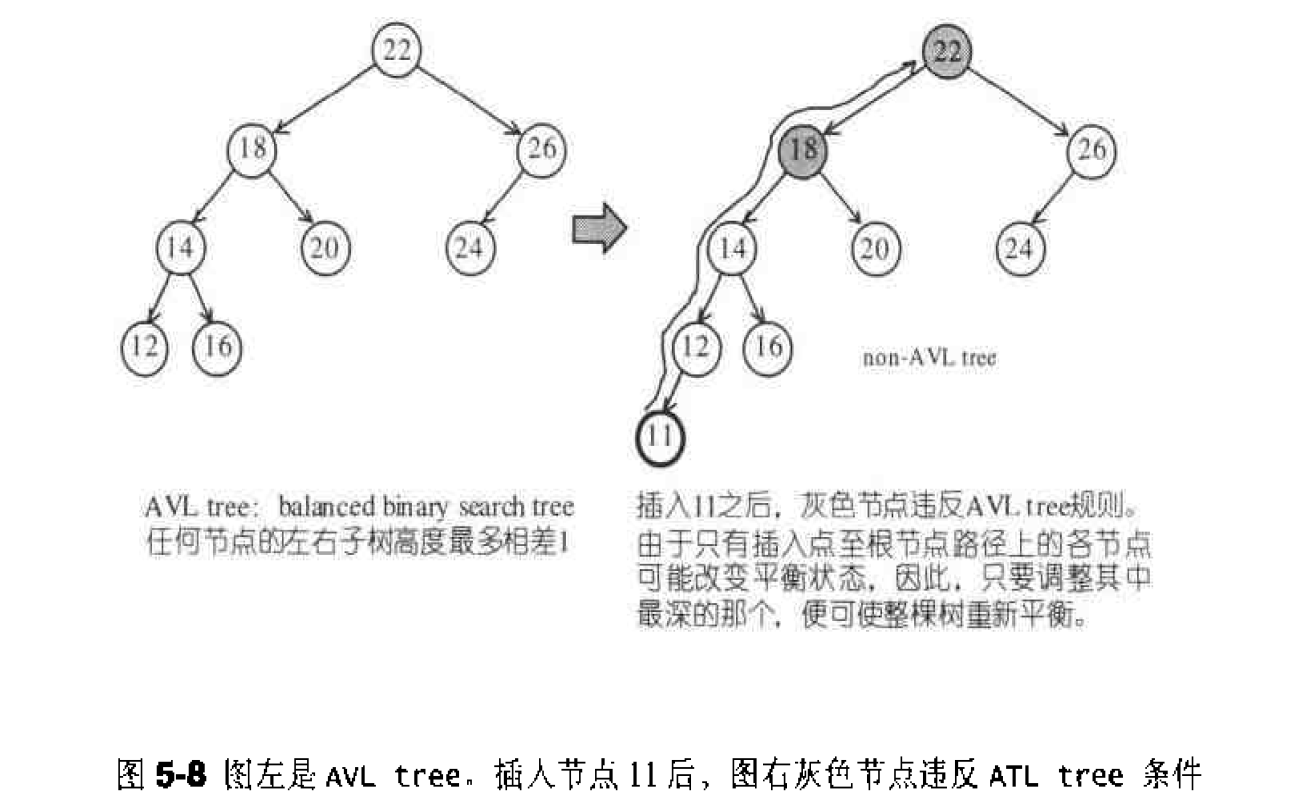
AVLtree是- -个“加上了额外平衡条件”的二叉搜索树。其平衡条件的建立是为了确保整棵树的深度为O(ogN)。直观上的最佳平衡条件是每个节点的左右子树有着相同的高度，但这未免太过严苛，我们很难插人新元素而又保持这样的平衡条件。AVLtree于是退而求其次，要求任何节点的左右子树高度相差最多1。这是一个较弱的条件，但仍能够保证“对数深度( logarithmic depth)”平衡状态。

图5-8左侧所示的是一个AvL tree，插入了节点11之后〔图右），灰色节点违反ATL tree 的平衡条件、由于只有“插入点至根节点”路径上的各节点可能改变平衡状态、因此，只要调整共中最深的那个节点，便可使整棵树重新获得平衡。

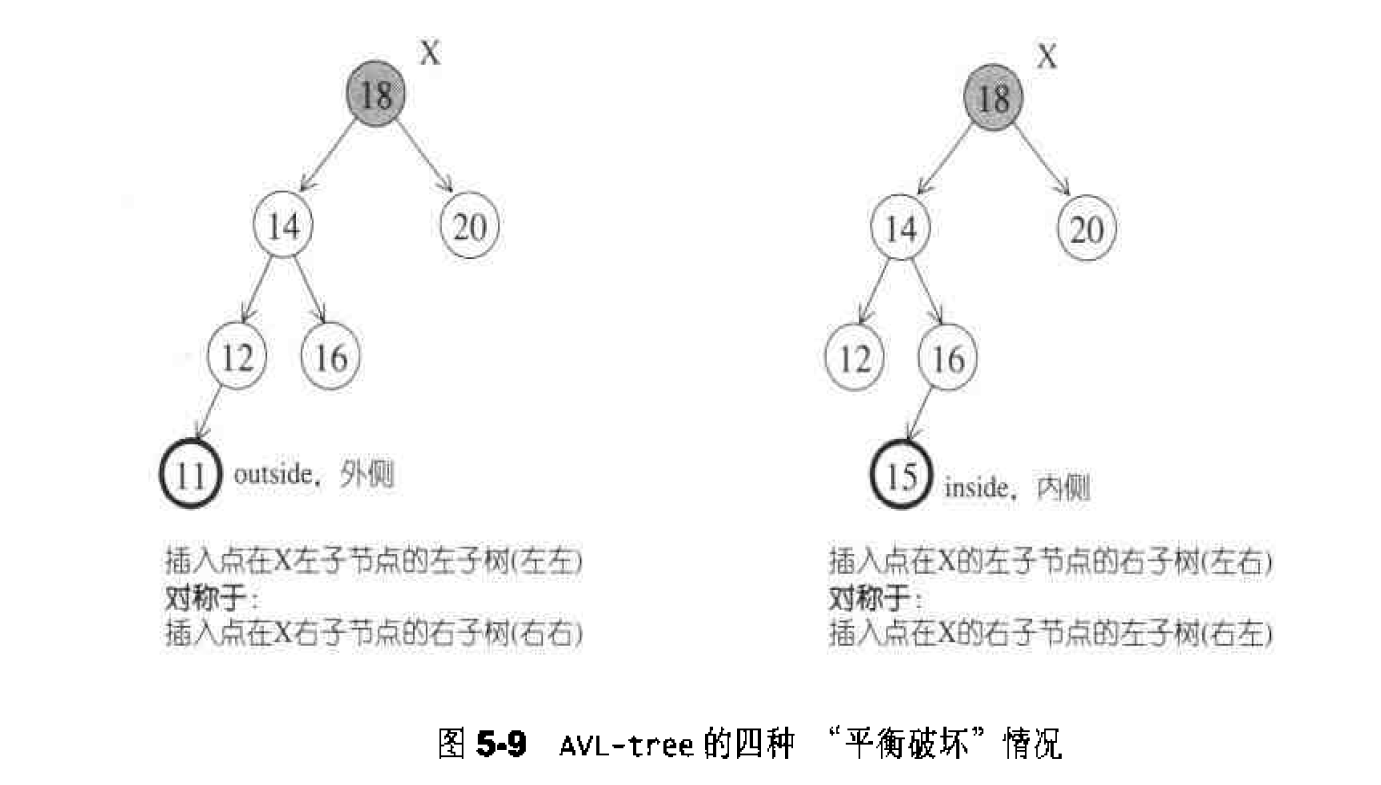
前面说过，只要调整“插人点至根节点”路径.上、平衡状态被破坏之各节点中最深的那–个，便可使整棵树重新获得平衡。假设该最深节点为X，由于节点最多拥有两个子节点，而所谓“平衡被破坏”意味着X的左右两棵子树的高度相差2，因此我们可以轻易将情况分为四种（图5-9) :

1.插入点位于X的左子节点的左子树——左左。
2.插入点位于X的左子节点的右子树——左右。
3.插人点位于X的右了节点的左子树——右左。
4.插人点位于X的右子节点的右子树——右右。

情况1,4彼此对称，称为外侧（ outside）插入，可以采用单旋转操作（ singlerotation）调整解决。情况2,3彼此对称，称为内侧(inside）插入，可以采用双旋转操作〔 double rotation）调整解决。

单旋转

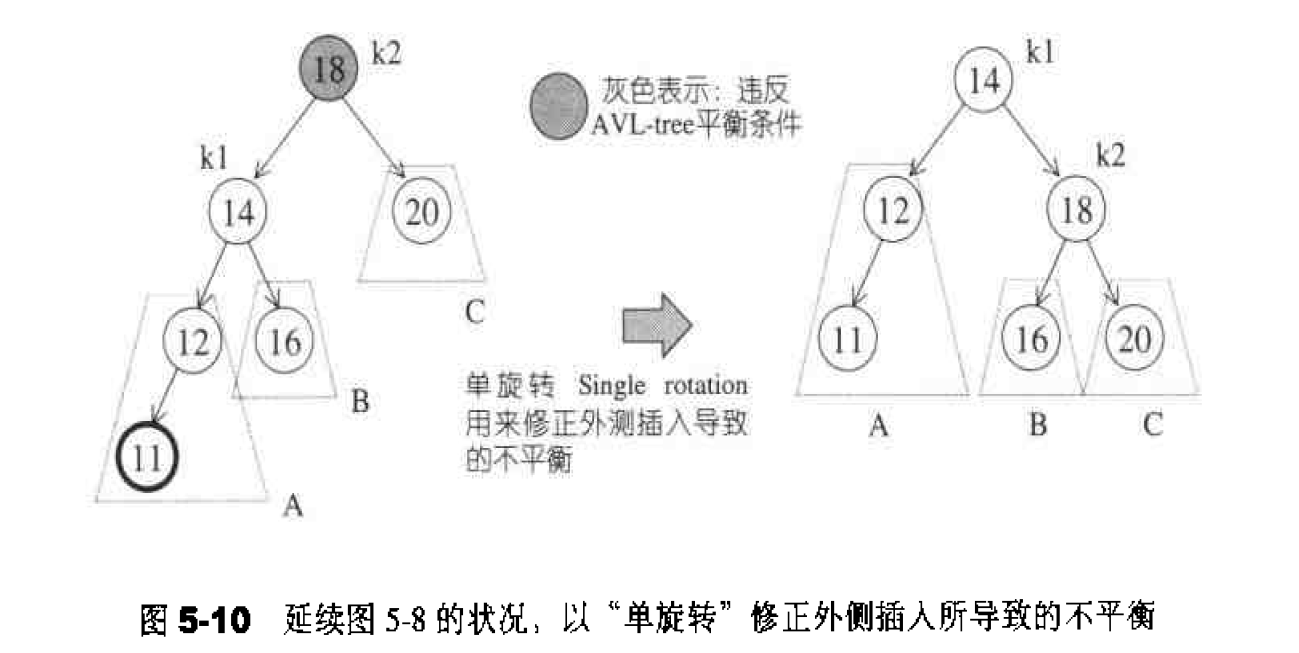
在外侧插入状态中,k2“插人前平衡，插入后不平衡”的唯―情况如图5-10左侧所示。A子树成长了一层，致使它比C子树的深度多2。B子树不可能和A子树位于同一层，否则k2在插人前就处于不平衡状态了。B子树也不可能和C子树位于同一层，否则第一个违反平衡条件的将是k1而不是k2。

为了调整平衡状态,我们希望将A子树提高一层,并将C子树下降一层一这t经比AVL-tree所要求的平衡条件更进一步了，图5-10右侧即是调整后的情况。我们可以这么想象、把k1向上提起，使k2自然下滑、并将B子树挂到k2的左侧。这么做是因为，二叉搜索树的规则使我们知道，k2 > kl，所以k2必须成为新树形中的kl的右子节点。二叉搜索树的规则也告诉我们，B子树的所有节点的键值都在k1和 k2之间，所以新树形中的B子树必须落在k2的左侧。

以上所有调整操作都只需要将指针稍做搬移,就可迅速达成。完成后的新树形符舍AVL.-tree的平衡条件,不需再做调整。
图5-10所显示的是“左左”外侧插人。至于“右右”外侧插人，情况如出一辙。

双旋转

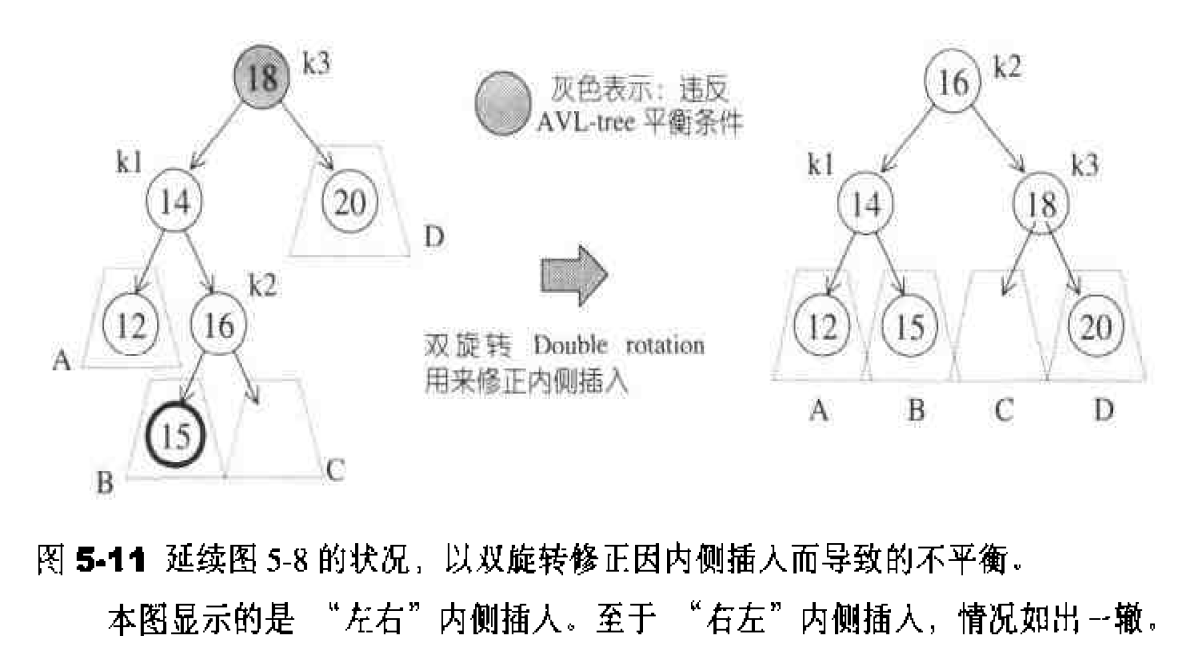
图5-11左侧为内侧插入所造成的不平衡状态。单旋转无法解决这种情况。第一，我们不能再以k3为根节点，其次，我们不能将k3和k1做一次单旋转，因为旋转之后还是不平衡（你不妨自行画图试试）。唯一的可能是以k2为新的根节点，这使得〔根据二叉搜索树的规则）k1必须成为k2的左子节点，k3必须成为k2的右子节点，而这么一来也就完全决定了四个子树的位置。新的树形满足 AVL-tree的平衡条件，并且，就像单旋转的情况一样，它恢复了节点插人之前的高度，因此保证不再需要任何调整。

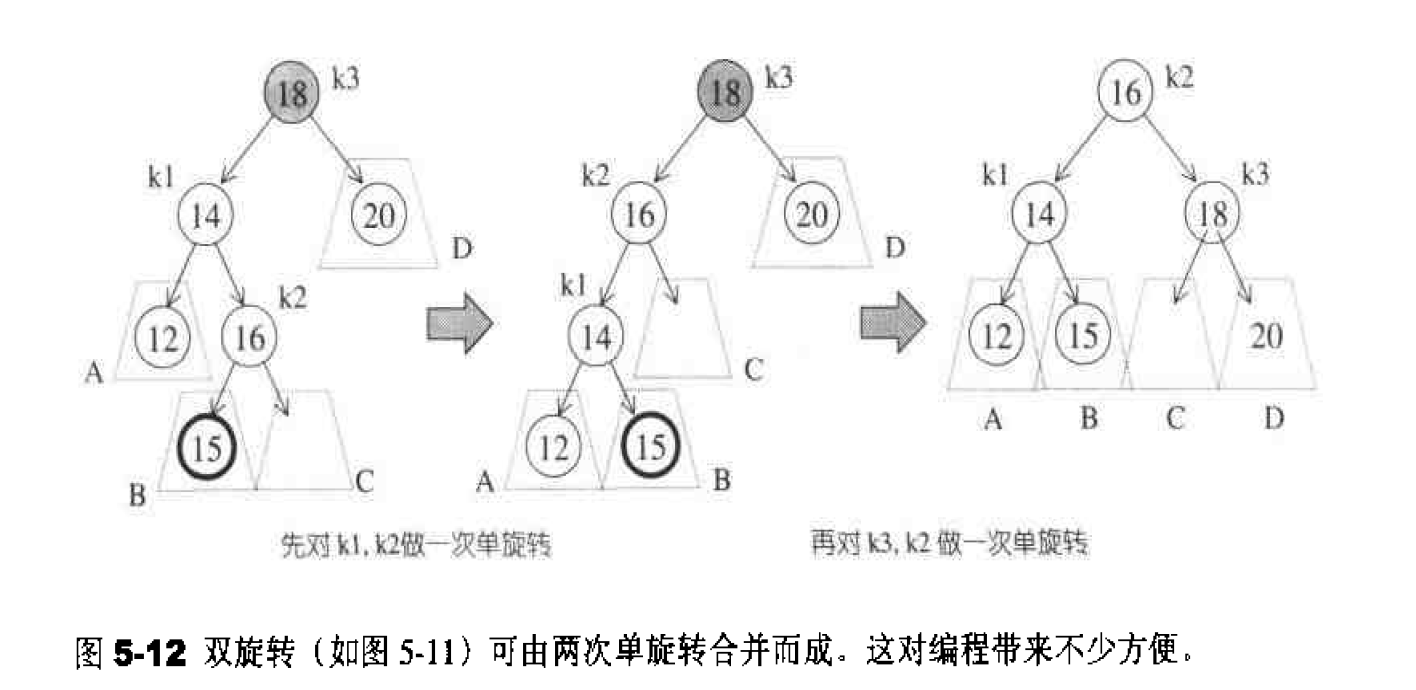
为什么称这种调整为双旋转呢?因为它可以利用两次单旋转完成，见图5-12。以上所有调整操作都只需要将指针稍做搬移，就可迅速达成。完成之后的新树形符合AVL-tree的平衡条件，不需再做调整。
图5-11显示的是“左右”内侧插人。至于“右左”内侧插人，情况如出辙。

RB-tree是另﹒个被广泛使用的平衡二叉搜索树，也是 SGI STL唯一实现的一种搜寻树,作为关联式容器( associated containers)的底部机制之用。RB-tree的平衡条件虽然不同于AVL-tree，但同样运用了单旋转和双旋转修正操作。

RB-Tree（红黑树）

AVL-tree之外，另一个颇具历史并被广泛运用的平衡二义搜索树是RB-tree(红黑树）．所谓RB-tree，不仅是﹒个二叉搜索树，而且必须满足以下规则:

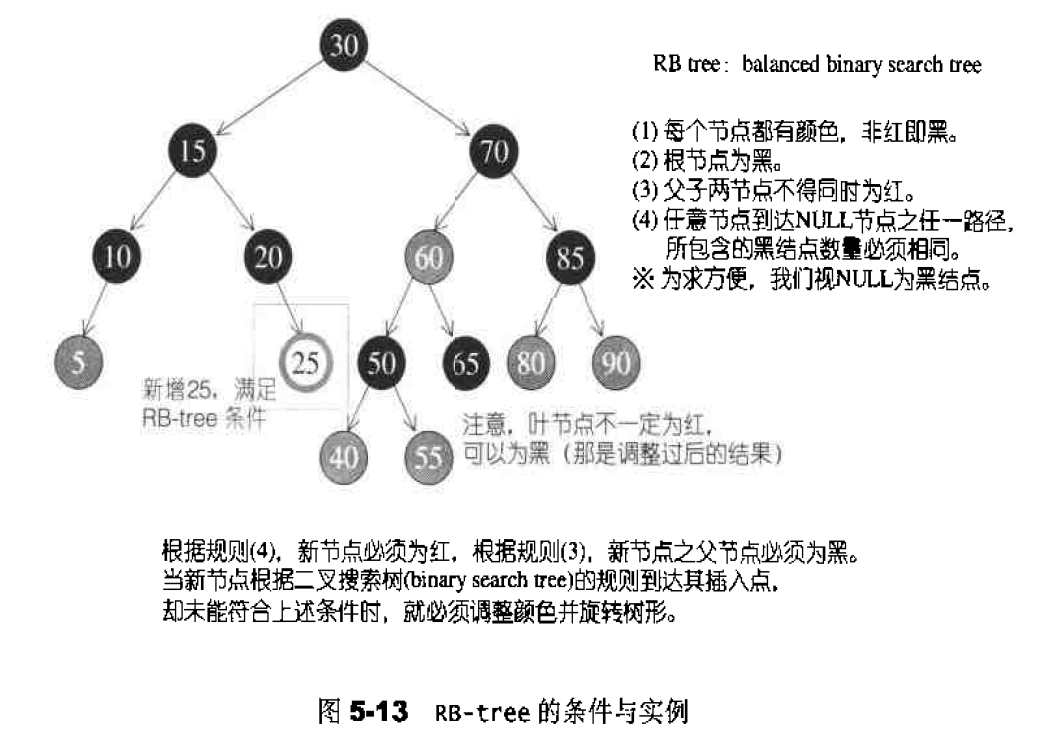
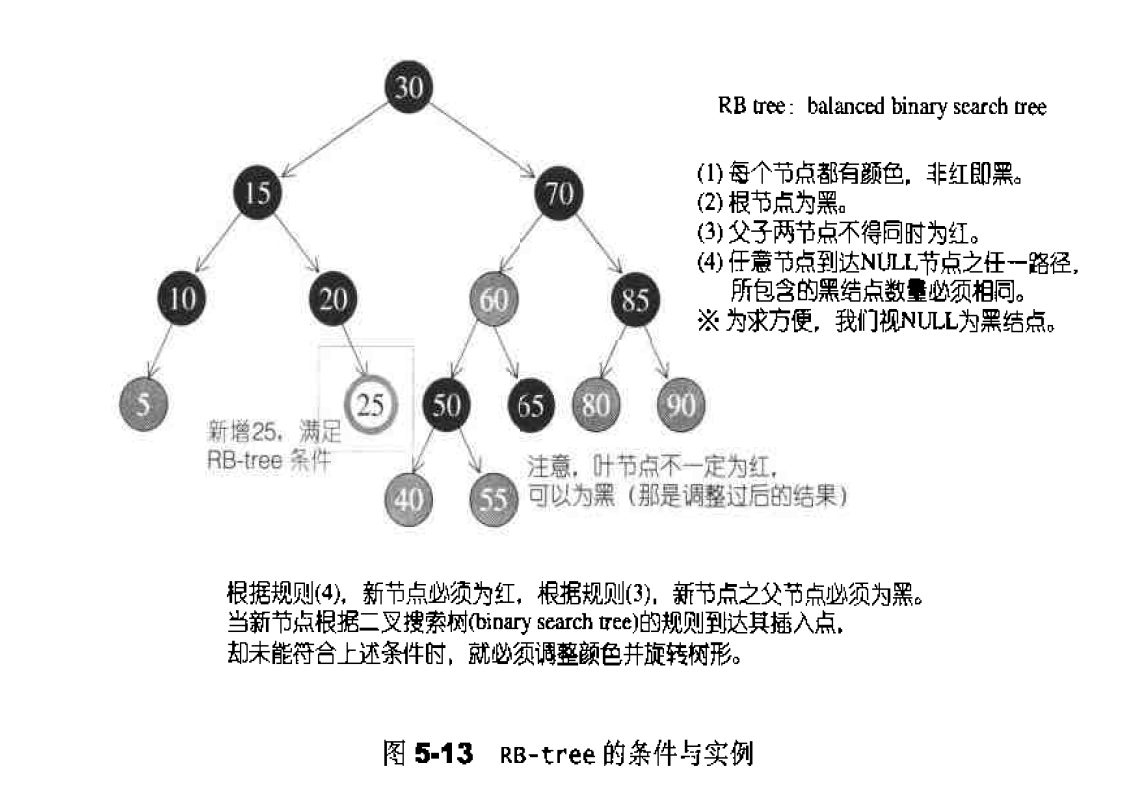
1.每个节点不是红色就是黑色（图中深色底纹代表黑色，浅色底纹代表红色，下同），
2.根节点为黑色。
3.如果节点为红，其子节点必须为黑。
4.任一节点至 NULL（树尾端）的任何路径，所含之黑节点数必须相同。

根据规则4，新增节点必须为红;根据规则3，新增节点之父节点必须为黑。当新节点根据二叉搜索树的规则到达其插入点，却未能符合上述条件时，就必须调整颜色并旋转树形。见图5-13说明。

红黑树太多内容了。。。。

set

set的特性是，所有元素都会根据元素的键值自动被排序。 set的元素不像map那样可以同时拥有实值 （value）和键值 (key) , set元素的键值就是实值，实值就是键值。set 不允许两个元素有相同的键值.

我们可以通过set的迭代器改变set的元素值吗?不行，因为set 元素值就是其键值，关系到set元素的排列规则。如果任意改变 set元素值，会严重破坏set 组织。稍后你会在set 源代码之中看到，set : :iterator被定义为底层RB-tree 的const_iterator，杜绝写人操作。换句话说，set iterators是一种constant iterators （相对于mutable iterators ) ,

我们可以通过set的迭代器改变set的元素值吗?不行，因为set 元素值就是其键值，关系到set元素的排列规则。如果任意改变set元素值，会严重破坏set组织。稍后你会在set源代码之中看到,set : :iterator被定义为底层RB-tree 的 const_iterator，杜绝写人操作。换句话说，set iterators是一种constant iterators(相对于mutable iterators).

set拥有与 list相同的某些性质:当客户端对它进行元素新增操作(insert）或删除操作（erase)时，操作之前的所有迭代器，在操作完成之后都依然有效。当然，被删除的那个元素的迭代器必然是个例外。

STL特别提供了一组set/multiset相关算法，包括交集set_intersection、联集set…urion、差集set_difference 、对称差集set_synmmnetric_difference，详见6.5节。

由于RB-tree是一种平衡二叉搜索树,自动排序的效果很不错,所以标准的STLset即以RB-tree为底层机制。又由于set所开放的各种操作接口，RB-tree 也都提供了,所以几乎所有的set操作行为、都只是转调用RB-tree的操作行为而已。

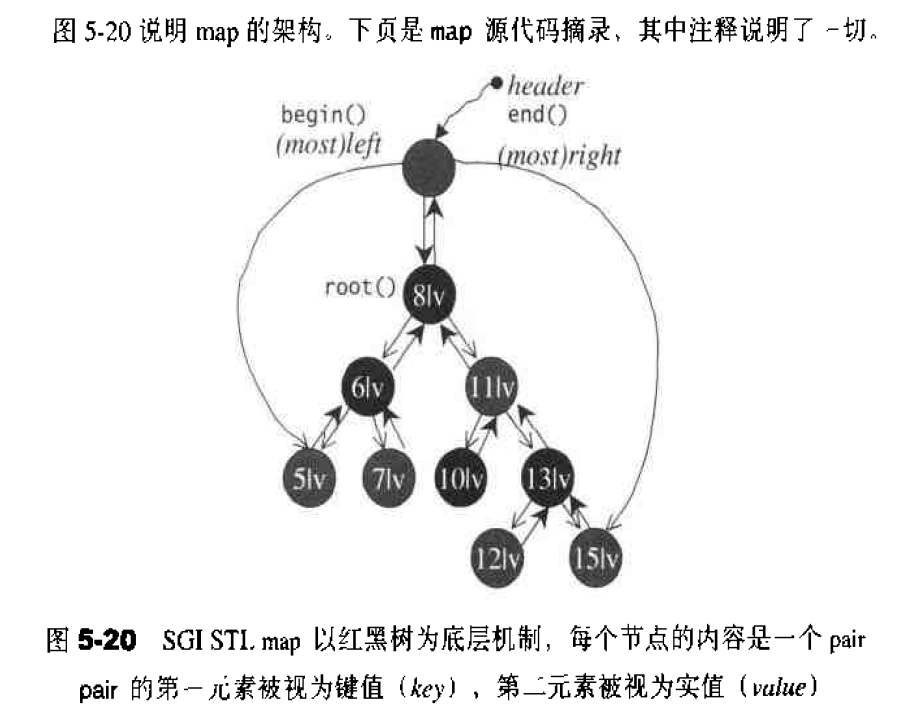
map

map的特性是，所有元素都会根据元素的键值自动被排序。map的所有元素都是 pair，同时拥有实值（value）和键值（key) . pair的第一元素被视为键值，第二元素被视为实值。map不允许两个元素拥有相同的键值。

我们可以通过map的迭代器改变map 的元素内容吗?如果想要修正元素的键值，答案是不行，因为map元素的键值关系到map元素的排列规则。任意改变map元素键值将会严重破坏map组织。但如果想要修正元素的实值，答案是可以．因为map元素的实值并不影响map元素的排列规则。因此，map iterators 既不是一种constant iterators，也不是一种 mutable iterators.

由丁RB-tree是一种平衡二叉搜索树,自动排序的效果很不错,所以标准的STLmap即以RB-tree为底层机制10、又由于map 所开放的各种操作接口，RB-tree也都提供了，所以见乎所有的map操作行为，都只是转调用RB-tree的操作行为而已。

multiset

multiset的特性以及用法和 set完全相同，唯一的差别在于它允许键值重复、因此它的插入操作采用的是底层机制 RB-tree 的 insert_equal( )而非insert_unique ( )。

multimap

multinap的特性以及用法与map完全相同，唯一的差别在于它允许键值重复，因此它的插人操作采用的是底层机制RB-tree 的 insert_equal () 而非不同之处:insert_unique()。

hashtable

二叉搜索树具有对数平均时间〔 logarithmic average tirne）的表现，但这样的表现构造在一个假设上:输入数据有足够的随机性。这﹒节要介绍一种名为hashtab1e(散列表）的数据结构，这种结构在插入、删除、搜寻等操作上也具有“常数平均时间”的表现，而且这种表现是以统计为基础，不需仰赖输人元素的随机性。

hash table可提供对任何有名项( narned item)的存取操作和删除操作。由于操作对象是有名项,所以hashtable也可被视为一种字典结构(dictionary)。这种结构的用意在于提供常数时间之基本操作，就像stack或queue那样。乍听之下这几乎是不可能的任务，因为约束制条件如此之少，而元素个数增加，搜寻操作必定耗费更多时间。

哈希冲突解决方案：

使用hash function会带来个问题:可能有不同的元素被映射到相同的位置(亦即有相同的索引)。这无法避免，因为元素个数大于array 容量。这便是所谓的“碰撞(coNlision)”问题。解决碰撞问题的方法有许多种，包括线性探测(Jinearprobing)、二次探测（quadratic probing)、开链(separate chaining
）…等做法。每种方法都很容易，导出的效率各不相同——与array的填满程度有很大的关连。

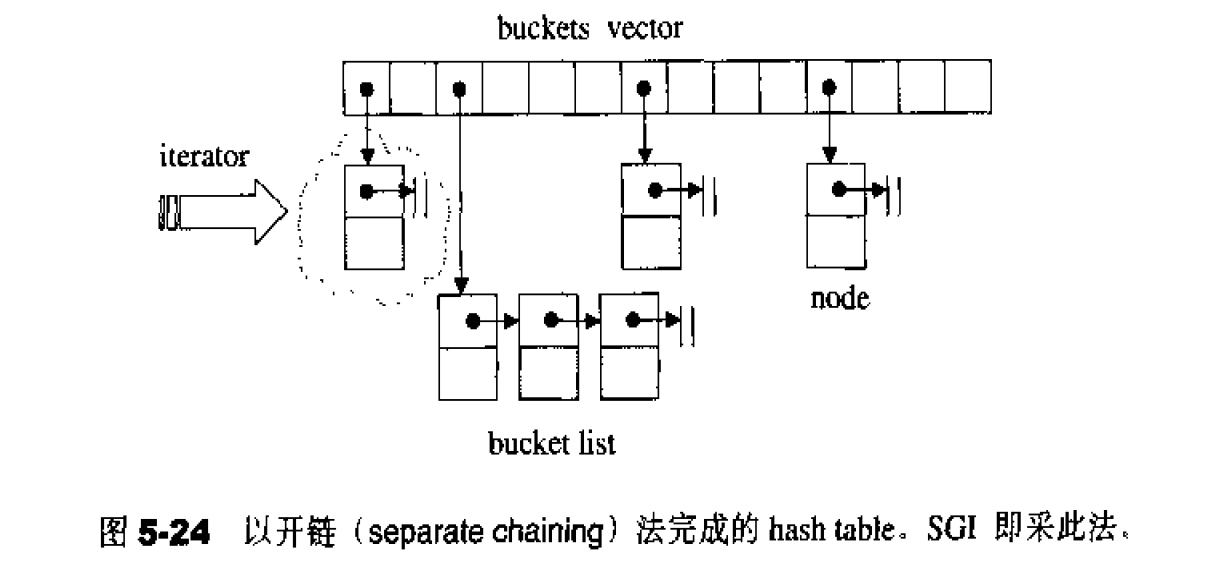
另一种与二次探测法分庭抗礼的，是所谓的开链(separate chaining)法。这种做法是在每一个表格元素中维护一个list: hash function为我们分配某–个list，然居我们在那个 1ist身上执行元素的插人、搜寻、删除等操作。虽然针对list而进行的搜寻只能是一种线性操作，但如果 1ist够短，速度还是够快。
使用开链手法，表格的负载系数将大于1.SGI STL的hash tabTe 便是采用这种做法，稍后便有详细的实现介绍。

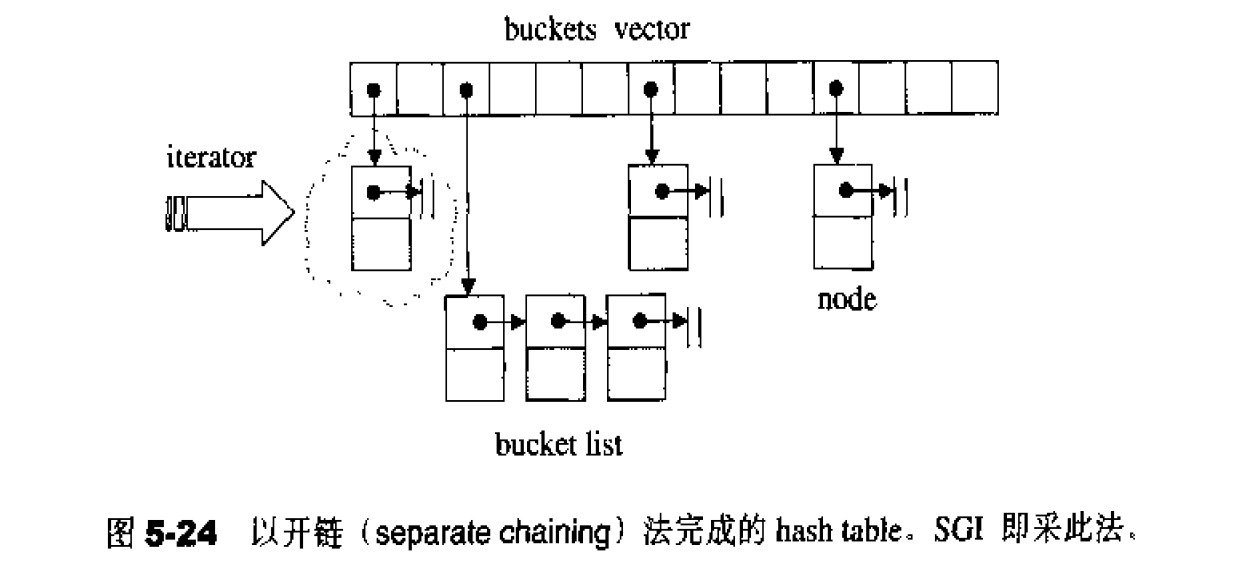
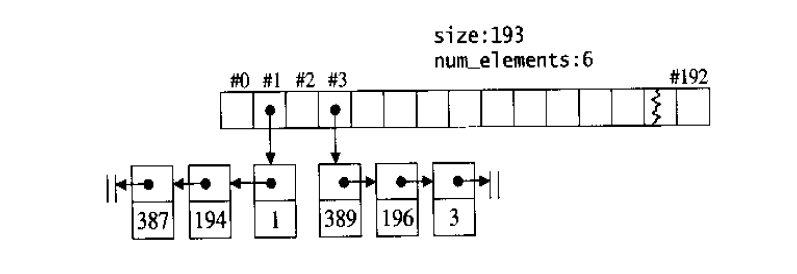
图5-24是以开链法( separate chaining〉完成hash table 的图形表述。为了解说sGI STL源代码，我遵循SGI的命名，称hash table表格内的元素为桶子( bucket),此名称的大约意义是，表格内的每个单元，涵盖的不只是个节点〔元素），甚且可能是一“桶”节点。

注意，bucket所维护的linked list，并不采用STL的 list或slist，而是自行维护上述的 hash table node。至于buckets聚合体，则以vector (4.2节）完成，以便有动态扩充能力。稍后在hash table 的定义式中我们可以清楚看到这一点。

请注意，hashtable 的迭代器没有后退操作（operator– ( )) , hashtable也没有定义所谓的逆向迭代器(reverse iterator) 。

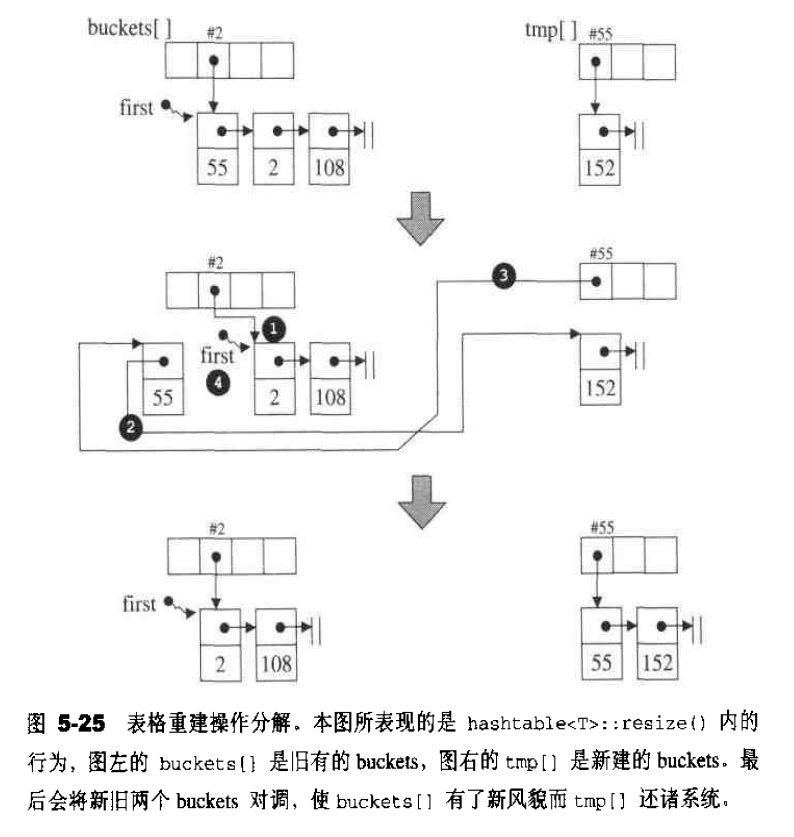
虽然开链法( separate chaining)并不要求表格大小必须为质数，但SGI STL仍然以质数来设计表格大小，并且先将28个质数〔逐渐呈现大约两倍的关系）计算好，以备随时访问，同时提供一个函数，用来查询在这28个质数之中，“最接近某数并大于某数”的质数:

hash_set

虽然STL只规范复杂度’与j接口，并不规范实现方法，但 STL set多半以RB-tree 为底层机制，SGI则是在STL标准规格之外另又提供了一个所谓的hash_set，以 hashtable 为底层机制。由于 hash_set所供应的操作接口，hashtable 都提供了，所以几乎所有的 hash_set操作行为，都只是转调用hashtable的操作行为而已。

运用set，为的是能够快速搜寻元素。这一点，不论其底层是RB-tree或是hashtable，都可以达成任务.但是请注意，RB-tree有自动排序功能面hashtable没有，反应出来的结果就是，set的元素有自动排序功能面hash_set没有。

set的元素不像map那样可以同时拥有实值（value）和键值(key ) , set元素的键值就是实值．实值就是键值。这一点在 hash_set中也是一样的。
hash_set 的使用方式和set完全相同。

hash_map

sGl 在STL标准规格之外，另提供了一个所谓的hash_map，以 hashtab1e为底层机制。由于hash_map所供应的操作接口，hashtable都提供了，所以几乎所有的hash_map操作行为，都只是转调用hashtable的操作行为而已。

运用map,为的是能够根据键值快速搜寻元素.这–点,不论其底层是RB-tree或是hashtable，都可以达成任务。但是请注意，RB-tree有自动排序功能而hashtable没有，反应出来的结果就是，map 的元素有自动排序功能而hash_map没有。

map的特性是，每一个元素都同时拥有一个实值（value)和一个键值(key).这一点在hash_map中也是一样的。hash_map的使用方式，和map完全相同。

hash_multiset

hashmultiset的特性与multiset完全相同，唯一的差别在于它的底层机制是hashtable。也因此，hash_multiset的元素并不会被自动排序。

hash.mu1tiset和 hash_set实现上的唯–差别在于,前者的元素插人操作采用底层机制hashtable的insert._equal( )，后者则是采用insert _unique ( ) .

hash _multimap

hash_nultimap的特性与multimap完全相同,唯一的差别在于它的底层机制是hashtable。也因此，hash_multimap的元素并不会被自动排序。

hashmultimap和 hash_map实现上的唯一差别在于,前者的元素插入操作采用底层机制hashtable的insert_equal()，后者则是采用inscrt_unique ( ) 。

6. 算法

7. 仿函数（functors）

详解链接

仿函数是早期的命名，C++标准规格定案后所采用的新名词是函数对象。

仿函数的作用主要在哪里?从第6章可以看出，STL所提供的各种算法，往往有两个版本。其中一个版本表现出最常用(或最直观）的某种运算，第二个版本则表现出最泛化的演算流程,允许用户“以template参数来指定所要采行的策略”。拿accumulate ()来说，其一般行为(第一版本)是将指定范围内的所有元素相加，第二版本则允许你指定某种“操作”,取代第一版本中的“相加”行为.再举sort ()为例，其第一版本是以operator<为排序时的元素位置调整依据，第二版本则允许用户指定任何“操作”，务求排序后的两两相邻元素都能令该操作结果为true。噢，是的，要将某种“操作”当做算法的参数，唯一办法就是先将该“操作”（可能拥有数条以上的指令）设计为一个函数，再将函数指针当做算法的一个参数;或是将该“操作”设计为一个所谓的仿函数（就语言层面而言是个class），再以该仿函数产生一个对象，并以此对象作为算法的一个参数。

根据以上陈述，既然函数指针可以达到“将整组操作当做算法的参数”，那又何必有所谓的仿丽数呢?原因在于函数指针毕竟不能满足STL对抽象性的要求，也不能满足软件积木的要求——函数指针无法和STL其它组件（如配接器adapter,第8章）搭配，产生更灵活的变化.

就实现观点而言，仿函数其实上就是一个“行为类似函数”的对象。为了能够“行为类似函数”，其类别定义中必须自定义（或说改写、重载）function call 运算子(operator ()，语法和语意请参考1.9.6节）。拥有这样的运算子后，我们就可以在仿函数的对象后而加上一对小括号,以此调用仿函数所定义的operator ( ),像这样:

STL仿函数的分类，若以操作数（ operand）的个数划分，可分为一元和二元仿函数，若以功能划分，可分为算术运算〔Arithmetic)、关系运算(Rational) 、逻辑运算（Logical）三大类。任何弯患酱赢你使用STL内建的仿函数，都必须含人<functionals头文件，SGI 则将它们实际定义于stl_tunction
.h>文件中。以下分别描述。

可配接（Adaptable）的关键

在STL六大组件中，仿函数可说是体积最小、观念最简单、实现最容易的一个。但是小兵也能立大功——它扮演一种“策略”2角色，可以让STL算法有更灵活的演出。面更加灵活的关键，在于STL仿函数的可配接性（adaptability )

算术类仿函数

关系类仿函数

逻辑类仿函数

8. 配接器（adapters）

配接器（ adapters）在STL组件的灵活组合运用功能上，扮演着轴承、转换器的角色。

STL所提供的各种配接器中,改变仿函数( functors )接口者,我们称为functionadapter，改变容器（containers）接口者，我们称为container adapter，改变迭代器( iterators）接口者，我们称为iterator adapter。

应用于容器container adapters

STL提供的两个容器 queue 和 stack，其实都只不过是一种配接器。它们修饰deque的接口而成就出另一种容器风貌.这两个container adapters已于第4
章介绍过。

应用于迭代器iterator adapters

STZ提供了许多应用于迭代器身上的配接器，包括insert iterators，reverseterators，iostream terators。C++ Standard 规定它们的接口可以藉由获得，SGI STL则将它们实际定义于<st1_iterator.h>.

所谓insert iterators，可以将一般迭代器的赋值（ assign）操作转变为插人( insert)·操作。这样的迭代器包括专司尾端插人操作的 back_insert_iterator,
专司头端插人操作的 front.insertiterator，以及可从任意位置执行插入操作
的inser…iterator.由于这三个iterator adapters的使用接口不是十分直观，给一般用户带来困扰，因此，STL更提供三个相应函数: back_inserter ( ) 、front_inserter(). inserter()，如图8-1所示，提升使用时的便利性。

所谓roverse iterators，可以将一般迭代器的行进方向逆转，使原本应该前进的operator++变成了后退操作，使原本应该后退的operator–变成了前进操作。这种错乱的行为不是为了掩人耳日或为了欺敌效果,而是因为这种倒转筋脉的性质运用在“从尾端开始进行”的算法上，有很大的方便性。稍后我有一些范例展示。

所谓iostream iterators，可以将迭代器绑定到某个iostream对象身上。绑定到istream对象（例如std::cin）身上的，称为 istream_iterator，拥有输人功能﹔绑定到ostream对象（例如std: :cout )身上的，称为ostream_iterator，拥有输出功能。这种迭代器运用于屏幕输出，非常方便。以它为蓝图，稍加修改，便可适用丁任何输出或输人装置上。例如，你可以在透彻了解iostream Rterators的技术后，完成-个绑定到Internet Explorer cache身上的迭代器，或是完成一个系结到磁盘目录上的一个迭代器.

应用于仿函数functor adapters

functor adapters（亦称为function adapters）是所有配接器中数量最庞大的一个族群，其配接灵活度也是前二者所不能及，可以配接、配接、再配接。这些配接操作包括系结（ bind)、否定(negate)，组合(compose)、以及对一般函数或成员函数的修饰（使其成为一个仿函数）。C++ Stadard规定这些配接器的接口可由获得，SGI STL则将它们实际定义于<stl_function.h> .

今天的文章STL源码刨析_宾州中文树 源码剖析分享到此就结束了，感谢您的阅读。