仿射变换算法_相似变换与仿射变换的区别

仿射变换（Affine Transformation）原理及应用

1 什么是仿射变换

• 仿射变换（Affine Transformation）其实是另外两种简单变换的叠加：一个是线性变换，一个是平移变换

• 仿射变换变化包括缩放（Scale、平移(transform)、旋转(rotate)、反射（reflection,对图形照镜子）、错切(shear mapping，感觉像是一个图形的倒影)，原来的直线仿射变换后还是直线，原来的平行线经过仿射变换之后还是平行线，这就是仿射

• 仿射变换中集合中的一些性质保持不变：
  （1）凸性
  （2）共线性：若几个点变换前在一条线上，则仿射变换后仍然在一条线上
  （3）平行性：若两条线变换前平行，则变换后仍然平行
  （4）共线比例不变性：变换前一条线上两条线段的比例，在变换后比例不变

2 仿射变换数学表达

一个集合 XX 的仿射变换为：
$$f(x)=Ax+b,x\in X$$

仿射变换是二维平面中一种重要的变换，在图像图形领域有广泛的应用，在二维图像变换中，一般表达为：
$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ 1\end{array}\right]=\left[\begin{array}{ccc}{R}_{00}& R_{01}& T_x\\ R_{10}& R_{11}& T_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]$$

可以视为线性变换R和平移变换T的叠加

3 仿射变换理解

要熟练应用仿射变换，则需先理解仿射变换，说白了就是要弄清楚上面的R，T矩阵各个参数代表什么含义，用图像来表达：

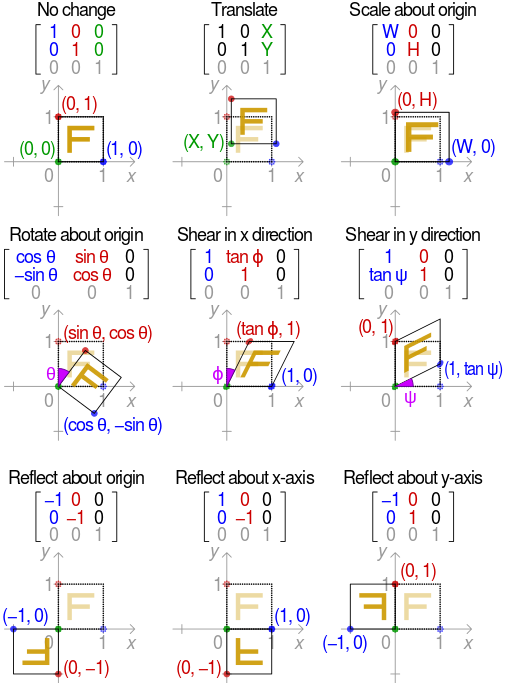
3.1 平移变换

不难想象，就是将x，y平移指定值，则R矩阵为单位矩阵，T矩阵为指定值，如上图中，第一行第二列图
$$M=\left[\begin{array}{ccc}1& 0& T_x\\ 0& 1& T_y\\ 0& 0& 1\end{array}\right]$$

3.2 反射变换

见图最后一行，如相对x轴放射，则x不变，y变为相反号
$$M=\left[\begin{array}{ccc}1& 0& 0\\ 0& -1& 0\\ 0& 0& 1\end{array}\right]$$

3.3 旋转变换

关于旋转矩阵，这里详细来看看，网上博客中，有朋友在疑惑旋转矩阵中，$sin\theta$的负号位置问题，下面我谈谈我个人想法，若有错误请大家指点。为简单起见，只从一个点的旋转来看

(1) 左下角为坐标原点

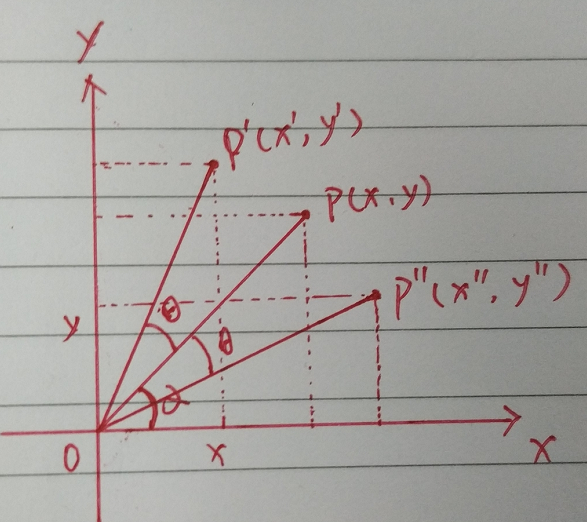
• 坐标原点为左下角
• 点$P(x,y)$为坐标系中一个点，与x轴的夹角为$\alpha$，假设其到原点的距离为1（方便计算）
• 点$P^{\prime }(x^{\prime },y^{\prime })$为P点逆时针旋转$\theta$角度的点
• 点$P^{\prime \prime }(x^{\prime \prime },y^{\prime \prime })$为P点顺时针旋转$\theta$角度的点

根据简单三角关系，可知
$$\{\begin{array}{l}x=cos\alpha \\ y=sin\alpha \end{array}$$
逆时针时：
$$\{\begin{array}{l}{x}^{\prime }=cos(\alpha +\theta )=cos\alpha \ast cos\theta -sin\alpha \ast sin\theta =x\ast cos\theta -y\ast sin\theta \\ y^{\prime }=sin(\alpha +\theta )=sin\alpha \ast cos\theta +cos\alpha \ast sin\theta =y\ast cos\theta +x\ast sin\theta \end{array}$$
则，逆时针旋转矩阵$R^{\prime }$为:
$$R^{\prime }=\left[\begin{array}{cc}cos\theta & -sin\theta \\ sin\theta & cos\theta \end{array}\right]$$

顺时针时：
$$\{\begin{array}{l}{x}^{\prime \prime }=cos(\alpha -\theta )=cos\alpha \ast cos\theta +sin\alpha \ast sin\theta =x\ast cos\theta +y\ast sin\theta \\ y^{\prime \prime }=sin(\alpha -\theta )=sin\alpha \ast cos\theta -cos\alpha \ast sin\theta =y\ast cos\theta -x\ast sin\theta \end{array}$$
则，顺时针旋转矩阵$R^{\prime \prime }$为:
$$R^{\prime \prime }=\left[\begin{array}{cc}cos\theta & sin\theta \\ -sin\theta & cos\theta \end{array}\right]$$

从上可以看出，这个负号位置问题，个人认为与旋转方向相关

（2）左上角为坐标原点

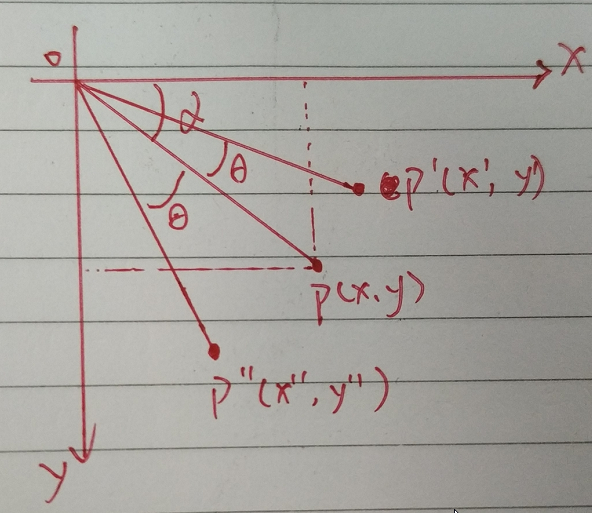
• 坐标原点为左上角
• 点$P(x,y)$为坐标系中一个点，与x轴的夹角为$\alpha$，假设其到原点的距离为1（方便计算）
• 点$P^{\prime }(x^{\prime },y^{\prime })$为P点逆时针旋转$\theta$角度的点
• 点$P^{\prime \prime }(x^{\prime \prime },y^{\prime \prime })$为P点顺时针旋转$\theta$角度的点

根据简单三角关系，可知
$$\{\begin{array}{l}x=cos\alpha \\ y=sin\alpha \end{array}$$
逆时针时：
$$\{\begin{array}{l}{x}^{\prime }=cos(\alpha -\theta )=cos\alpha \ast cos\theta +sin\alpha \ast sin\theta =x\ast cos\theta +y\ast sin\theta \\ y^{\prime }=sin(\alpha -\theta )=sin\alpha \ast cos\theta -cos\alpha \ast sin\theta =y\ast cos\theta -x\ast sin\theta \end{array}$$
则，逆时针旋转矩阵$R^{\prime }$为:
$$R^{\prime }=\left[\begin{array}{cc}cos\theta & sin\theta \\ -sin\theta & cos\theta \end{array}\right]$$

顺时针时：
$$\{\begin{array}{l}{x}^{\prime \prime }=cos(\alpha +\theta )=cos\alpha \ast cos\theta -sin\alpha \ast sin\theta =x\ast cos\theta -y\ast sin\theta \\ y^{\prime \prime }=sin(\alpha +\theta )=sin\alpha \ast cos\theta +cos\alpha \ast sin\theta =y\ast cos\theta +x\ast sin\theta \end{array}$$
则，顺时针旋转矩阵$R^{\prime \prime }$为:
$$R^{\prime \prime }=\left[\begin{array}{cc}cos\theta & -sin\theta \\ sin\theta & cos\theta \end{array}\right]$$

从上可以看出，这个负号位置问题，不但与旋转方向有关，还与原点有关

（3）总结

• 旋转矩阵R中，$sin\theta$的负号位置与旋转方向和原点相关
• 当记逆时针为正，左上角为原点时（opencv默认），旋转矩阵为：
  $$R=\left[\begin{array}{cc}cos\theta & sin\theta \\ -sin\theta & cos\theta \end{array}\right]$$

3.4 opencv中的仿射矩阵

getRotationMatrix2D函数

CV_EXPORTS_W Mat getRotationMatrix2D( Point2f center, double angle, double scale )

该函数是来计算仿射矩阵:

$$\left[\begin{array}{ccc}\alpha & \beta & (1-\alpha )\cdot \text{center.x}-\beta \cdot \text{center.y}\\ -\beta & \alpha & \beta \cdot \text{center.x}+(1-\alpha )\cdot \text{center.y}\end{array}\right]$$

其中

$$\begin{array}{l}\alpha =\text{scale}\cdot \cos \text{angle},\\ \beta =\text{scale}\cdot \sin \text{angle}\end{array}$$

• center：源图旋转中心

• angle： 旋转角度，用角度表示；逆时针旋转为正（坐标原点设为左上角）

   Rotation angle in degrees. 
   Positive values mean counter-clockwise rotation (thecoordinate origin is assumed to be the top-left corner).
  

• scale：各向同比缩放因子

• 源码

   	cv::Mat cv::getRotationMatrix2D( Point2f center, double angle, double scale )
   	{
   	    CV_INSTRUMENT_REGION();
   	
   	    angle *= CV_PI/180;
   	    double alpha = std::cos(angle)*scale;
   	    double beta = std::sin(angle)*scale;
   	
   	    Mat M(2, 3, CV_64F);
   	    double* m = M.ptr<double>();
   	
   	    m[0] = alpha;
   	    m[1] = beta;
   	    m[2] = (1-alpha)*center.x - beta*center.y;
   	    m[3] = -beta;
   	    m[4] = alpha;
   	    m[5] = beta*center.x + (1-alpha)*center.y;
   	
   	    return M;
   	}
  

• 矩阵由来：首先将轴心(x,y)移到原点，然后做旋转缩放变换，最后再将图像的左上角转换为原点
  $$M=\left[\begin{array}{ccc}1& 0& x\\ 0& 1& y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}cos\theta & sin\theta & 0\\ -sin\theta & cos\theta & 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}s& 0& 0\\ 0& s& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{ccc}1& 0& -x\\ 0& 1& -y\\ 0& 0& 1\end{array}\right]$$

4 参考文献

[1]仿射变换详解 warpAffine ：https://www.cnblogs.com/dupuleng/articles/4055020.html
[2]仿射变换（Affine transformation）: https://blog.csdn.net/robert_chen1988/article/details/80498805
[3]opencv学习(三十五)之仿射变换warpAffine: https://blog.csdn.net/keith_bb/article/details/56331356

今天的文章仿射变换算法_相似变换与仿射变换的区别分享到此就结束了，感谢您的阅读。