一.概念
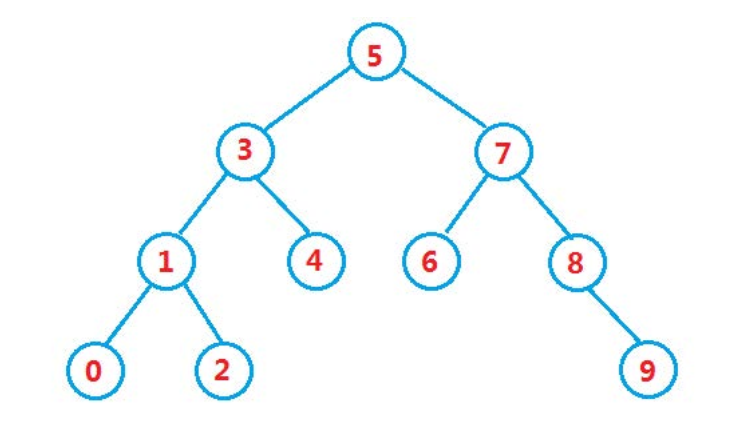
二叉搜索树又称二叉排序树,具有以下性质:
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树
注意:二叉搜索树中序遍历的结果是有序的
二、基本操作
1.查找元素
思路:二叉搜索树的左子树永远是比根节点小的,而它的右子树则都是比根节点大的值。当前节点比要找的大就往左走,当前元素比要找的小就往右走
public Node search(int key) {
if(root == null) {
return null;
}
Node cur = root;
while (cur != null) {
if(cur.val == key) {
return cur;
}else if(cur.val > key) {
cur = cur.left;
}else{
cur = cur.right;
}
}
return null;
}
2.插入元素
如果是空树直接把元素插入root位置就好了
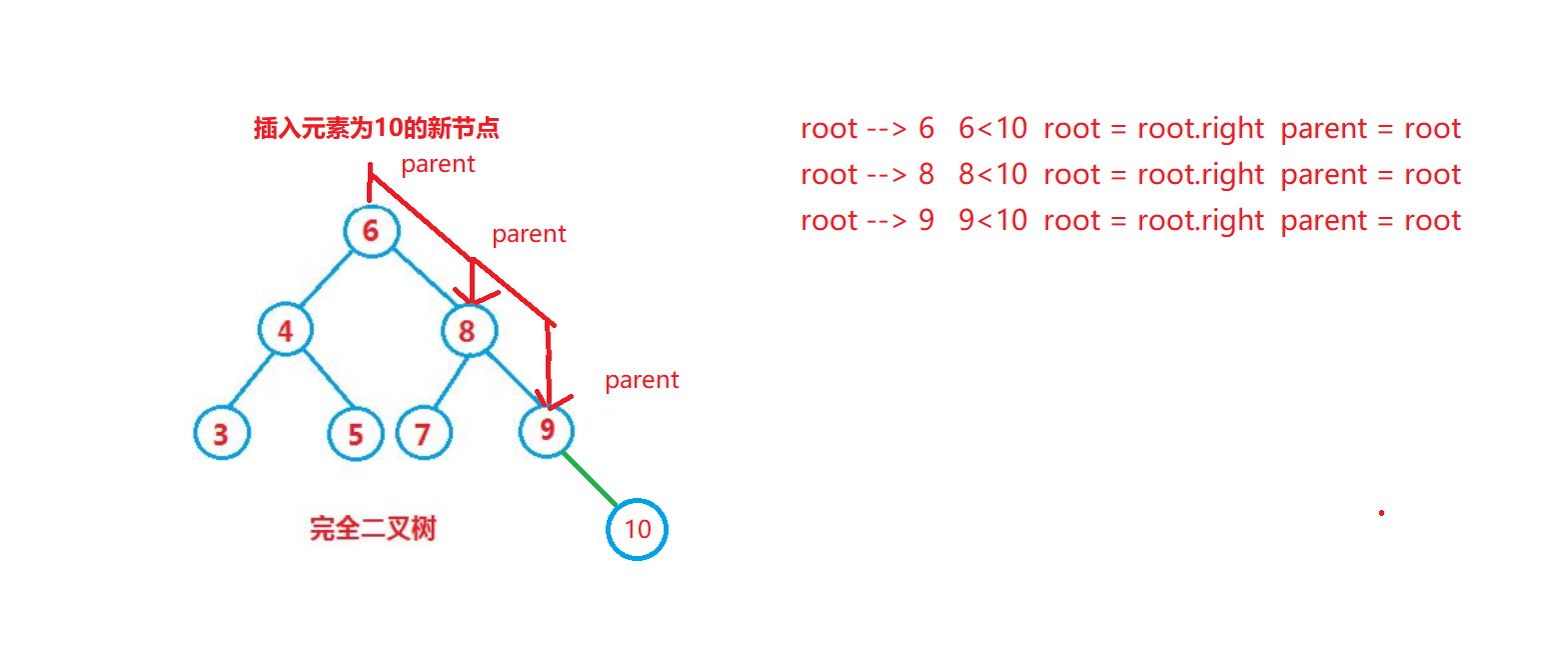
思路:因为是二叉搜索树就不能插入重复的元素了,且每次插入都是插入到叶子节点的位置。定义一个 cur 从root开始,插入的元素比当前位置元素小就往左走,比当前位置元素大就往右走,直到为空,所以就需要再定义一个变量parent 记住 cur 的前面的位置。
最后再判断插入到parent 的左子树还是右子树位置
代码实现:
public boolean insert(int key) {
Node node = new Node(key);
if(root == null) {
this.root = node;
return true;
}
Node parent = null;
Node cur = root;
while (cur != null) {
if(cur.val == key) {
//有相同的元素直接return
return false;
}else if(cur.val > key) {
parent = cur;
cur = cur.left;
}else{
parent = cur;
cur = cur.right;
}
}
if (parent.val > key) {
parent.left = node;
}else{
parent.right = node;
}
return true;
}
3.删除元素
删除元素是一个比较难的点,要考虑到很多种情况
-
cur.left == null
- cur 是 root,则 root = cur.right
- cur 不是 root,cur 是 parent.left,则 parent.left = cur.right
- cur 不是 root,cur 是 parent.right,则 parent.right = cur.right
-
cur.right == null
- cur 是 root,则 root = cur.left
- cur 不是 root,cur 是 parent.left,则 parent.left = cur.left
- cur 不是 root,cur 是 parent.right,则 parent.right = cur.left
-
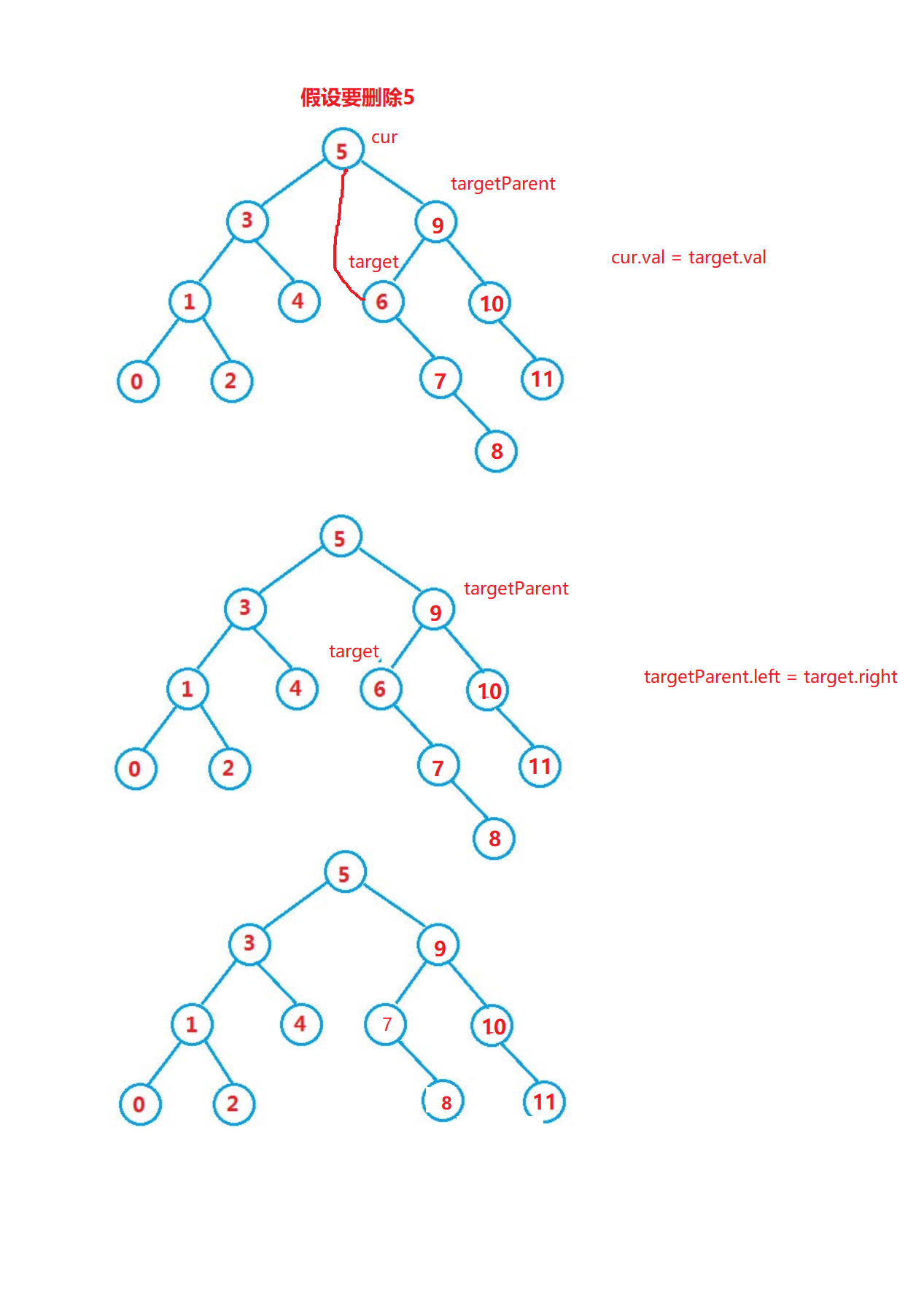
cur.left != null && cur.right != null
采用替罪羊的方式删除- 找到要删除节点,右树最左边的节点或者找到左树最右边的节点,替换这个两个节点的val值。
- 这样才能保证,删除后左树一定比根节点小,右树一定比根节点大
public boolean remove(int key) {
if(this.root == null) {
return false;
}
Node parent = null;
Node cur = this.root;
while (cur != null) {
if(cur.val == key) {
removeKey(parent,cur);
return true;
}else if(cur.val < key) {
parent = cur;
cur = cur.right;
}else{
parent = cur;
cur = cur.left;
}
}
return false;
}
public void removeKey(Node parent,Node cur) {
if(cur.left == null) {
if(cur == this.root) {
this.root = this.root.right;
}else if(cur == parent.left) {
parent.left = cur.right;
}else{
parent.right = cur.right;
}
}else if(cur.right == null) {
if(this.root == cur) {
this.root = this.root.left;
}else if(cur == parent.left) {
parent.left = cur.left;
}else{
parent.right = cur.left;
}
}else{
//左右都不为空的情况
Node targetParent = cur;
Node target = cur.right;
while (target.left != null) {
targetParent = target;
target = target.left;
}
cur.val = target.val;
if(targetParent.left == target) {
targetParent.left = target.right;
}else{
targetParent.right = target.right;
}
}
}
4.性能分析
插入和删除操作都必须先查找,查找效率代表了二叉搜索树中各个操作的性能
对有n个结点的二叉搜索树,若每个元素查找的概率相等,则二叉搜索树平均查找长度是结点在二叉搜索树的深度的函数,即结点越深,则比较次数越多。
但对于同一个关键码集合,如果各关键码插入的次序不同,可能得到不同结构的二叉搜索树:
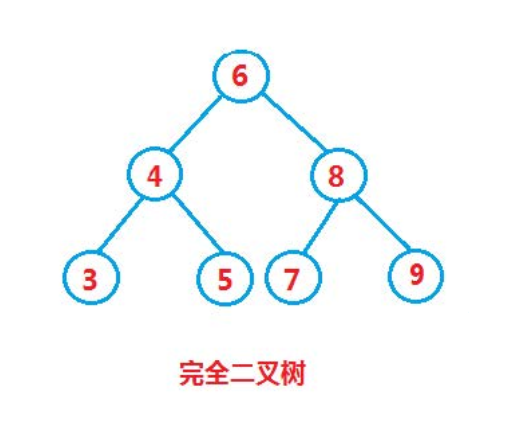
最好情况:二叉搜索树为完全二叉树,其平均比较次数为 O(log 2 _2 2n)
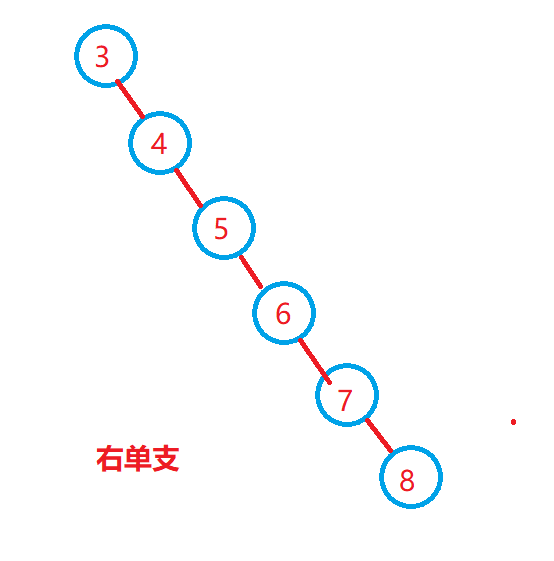
最坏情况:二叉搜索树退化为单支树,其平均比较次数为:O(n)
所有代码:
public class BinarySearchTree {
public static class Node {
int val;
Node left;
Node right;
public Node(int val) {
this.val = val;
}
}
public Node root = null;
/** * 查找某个节点 * @param key */
public Node search(int key) {
if(root == null) {
return null;
}
Node cur = root;
while (cur != null) {
if(cur.val == key) {
return cur;
}else if(cur.val > key) {
cur = cur.left;
}else{
cur = cur.right;
}
}
return null;
}
/** * 插入元素 * @param key * @return */
public boolean insert(int key) {
Node node = new Node(key);
if(root == null) {
this.root = node;
return true;
}
Node parent = null;
Node cur = root;
while (cur != null) {
if(cur.val == key) {
//有相同的元素直接return
return false;
}else if(cur.val > key) {
parent = cur;
cur = cur.left;
}else{
parent = cur;
cur = cur.right;
}
}
if (parent.val > key) {
parent.left = node;
}else{
parent.right = node;
}
return true;
}
/** * 删除元素 * @param key */
public boolean remove(int key) {
if(this.root == null) {
return false;
}
Node parent = null;
Node cur = this.root;
while (cur != null) {
if(cur.val == key) {
removeKey(parent,cur);
return true;
}else if(cur.val < key) {
parent = cur;
cur = cur.right;
}else{
parent = cur;
cur = cur.left;
}
}
return false;
}
public void removeKey(Node parent,Node cur) {
if(cur.left == null) {
if(cur == this.root) {
this.root = this.root.right;
}else if(cur == parent.left) {
parent.left = cur.right;
}else{
parent.right = cur.right;
}
}else if(cur.right == null) {
if(this.root == cur) {
this.root = this.root.left;
}else if(cur == parent.left) {
parent.left = cur.left;
}else{
parent.right = cur.left;
}
}else{
Node targetParent = cur;
Node target = cur.right;
while (target.left != null) {
targetParent = target;
target = target.left;
}
cur.val = target.val;
if(targetParent.left == target) {
targetParent.left = target.right;
}else{
targetParent.right = target.right;
}
}
}
}
今天的文章二叉搜索树二叉排序树二叉查找树_什么叫完全二叉树分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/74644.html