带你深入理解矩阵乘法的方法_矩阵的相乘计算方法「建议收藏」

为了不浪费大家宝贵的时间，开头我先简要说明一下这篇博文对哪些读者可能会有帮助

1、你是正在学习矩阵的乘法运算，觉得矩阵的乘法掌握起来很困难

2、你已经学会了矩阵乘法，但如果你在计算矩阵乘法时还在使用“一行乘一列得一数”的方法，那我强烈建议你看看后面的内容。

因为，我将带你更加深刻地理解矩阵，与之而来是对矩阵乘法的全新计算方式。这不仅让你在计算矩阵乘法时更快，而且更省心。

“矩阵就是数表”这可能是很多人第一次在线性代数课堂上听到的概念。我不能指责老师这样教有错，但这种肤浅的理解会给以后的学习带来越来越多的困难，无形之中让线性代数变得越来越“玄学”。

我认为好的学问都应该是通俗易懂的，因此让我们从一个最简单的概念开始——数数，或者说计量。

人类利用数字来表示事物的多少，但单有数字还是不够的，配合数字一起使用的还有一个概念——单位。例如，2L水，3kg钢铁等等。在更为抽象一点的事物上，还有与“单位”对应的一个概念——权。例如十进制数字 34 中的 4 的权是 1，而 3 的权是进制 10。简单来说，衡量任何实物，我们总是要现在此类事物中找一个看得顺眼的 “样品” 来作为衡量该类型其他事物的一个标准，看看需要衡量的事物是这个标准量的“几倍”，这样综合起来，我们心里就能有一个感性的认识。

认识一：其实没有标准，所有的标准都是由一个具体的事物（看得最顺眼的那个）来充当的。

上面的数数的例子都是单维度的，然而有很多量无法单单使用一对“数字+单位”这样的组合来描述清楚，而是需要多组。比如，平面上的点的位置需要两组，三维空间中的点的位置需要三组才能描述清楚，等等。而线性代数研究的就是空间。让我们还是再从最简单的概念开始——平面直角坐标系。

也许你会说，平面直角坐标系还不简单么，不就是这个么

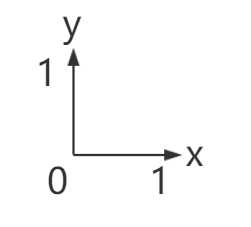
但是，我更希望它在你心中样子长成这样：

官方的说法把它叫做“平面直角坐标系的基”，你可以把它理解为在平面中数点的位置时用到的“单位”（就叫它“标准1”吧）。点（2,3）实际上是：

很多时候我们看的顺眼事物往往就那一个，因此标准也是唯一的了。比如二维平面的标准：

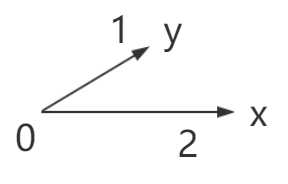
或许有人会说，x方向的基并不一定需要和y方向上的基保持长度相同，夹角也不需要是直角（只要是两个方向就行了）。随便整一个：

这也能作为衡量平面中点的坐标的“单位”（暂且叫它“标准2”好了）。但让我们来看一个具体的例子：

如果有一个点在上面这个坐标系中的坐标是：x=3, y=4。我们是不是通常会“忍不住“计算一下：

这个算式很简单，但不知你想过没有，为什么我们要去算呢？为什么不就用

来表示这个点的坐标就好了呢，实际上，当我们写下第一个等号，在进行

这样的换算时，我们就已经放弃上面的“标准2”，又使用起了平面直角坐标系的“标准1”。

认识二：标准往往是唯一的，使用其他的标准时，我们会情不自禁地回到这个唯一的标准。而这个唯一的标准都有一个特性，你不会去想把它转化成其他标准。

而这个的简单算式，实际上就是一次“矩阵运算”！不信？让我们再来看一下这个简单的式子：

这就是简单而又直接的算法，我可没有用什么“一横乘一竖”。不过你应该能发现两种算法的答案居然是一样的！等等，你也许会说，这根本就不是矩阵的乘法，就算你这样变形着写，着充其量也就是个向量对矩阵的乘法。那下面再让我们来思考一个更为深刻的问题——矩阵究竟是什么？是数表么，当然不是。其实，上文已经对这个问题给出了答案，再看看 认知一 吧，标准是由事物来充当的；二维空间中衡量点的位置的标准是由二维点来充当的，n 维空间中衡量点的位置的标准是由 n 维点来充当的。更进一步的，n 维空间中衡量一个点的坐标需要描述清楚 n 个维度，那描述清楚每一个维度又需要什么呢？回到开篇所说，需要一个数，一个“单位”。而在 n 维空间中，一个“单位”，一个“标准”，就是由一个点来充当的啊。即，一个维度需要一个标准，一个标准就是一个点，n 个维度自然需要 n 个点，而这每个点又都是 n 维空间中的点，自然每个都有 n 个维度。n 个 n 维点，可不就是一个  的矩阵嘛。为什么长宽相等的矩阵出现频率这么高，因为这样的矩阵本质上是一个坐标系！一个描述 n 维空间的坐标系。

当你用一个点（专业的说法叫向量）乘以矩阵时，实际上是放弃了以这个矩阵作为坐标系来衡量这个点的位置，重新使用了我们看得最顺眼的衡量标准——“单位阵”；

当你用矩阵乘以矩阵时，如

实际上是进行了 n 次点乘以矩阵。你放弃了用矩阵 B 来衡量前面矩阵 A 中的 n 个点的位置，重新使用了我们看得最顺眼的衡量标准——“单位阵”。这矩阵A中的 n 个点在矩阵 B 中的位置就是矩阵 A 本身所描述的，在你放弃标准 B（进行了这次矩阵运算后），矩阵 A 中的 n 个点的位置变成由矩阵 C 来描述了。

最后，有了上面的铺垫，我们来看一下，在这样的理解下，矩阵乘法到底应该怎么算。

这里只有“横”，没有什么“竖”的概念。不要一个数一个数地算，应该一个点一个点的算。公式太抽象？举个栗子,要计算：

我们一行一行的算，第一行：

相信剩下两行的计算就不用我啰嗦了，大家都会。

相信大家在学线性代数的时候，一会儿是列向量，一会儿是行向量，叫人头晕，老师解释这只是种写法，并没有什么讲究，但事实又好像不是如此，因为你要“一行乘一列”嘛，前面放“行”后面放“列”，这式子没法算呐。但我在这里要呐喊：

认识三：从来就没有什么列向量，所有的向量都是行向量。

其实，你要是认为“从来就没有什么行向量，所有的向量都是列向量”也可以，那样的算法是一次算一列。事情的真相其实是所有的向量都是“同方向”的，你喜欢行向量就都是行向量好了，你喜欢列向量就都是列向量好了，反正他们不会同时存在。相信只有一个方向的向量会让你神清气爽，不再晕头转向。不过你要是用列向量的话，记得要从后往前算，有兴趣的读者可以研究一下具体的算法，如有不明之处可以下面留言交流。

最后再皮一下：其实我是喜欢都看成行向量的，一来写起来省纸又顺手，二来从左往右算，符合习惯。我还暗自揣测过为什么行比列顺手，可能跟书写工具有关吧，矩阵记号是西方发明的，西方人用硬笔，书写时沉腕，旋转肘关节自然横向方便，如果矩阵记号是中国人发明的，我们用软笔，书写时悬腕，旋转肩关节自然竖向方便，那说不定矩阵运算就是列运算更加方便了。

如果您觉得本篇文章对您有所帮助，那就支持我一下吧。

今天的文章带你深入理解矩阵乘法的方法_矩阵的相乘计算方法「建议收藏」分享到此就结束了，感谢您的阅读。