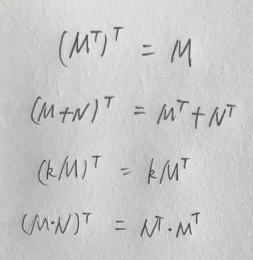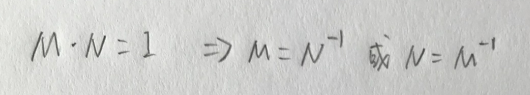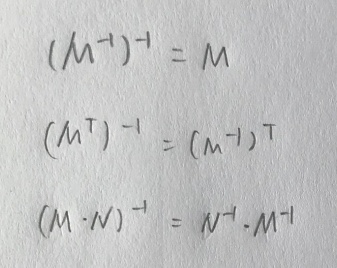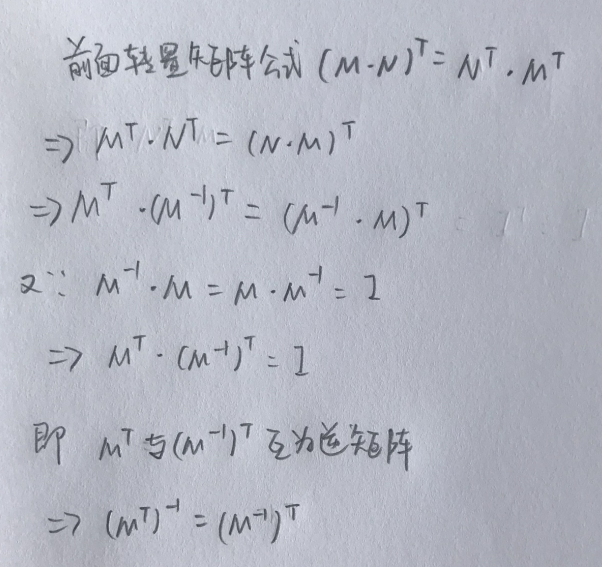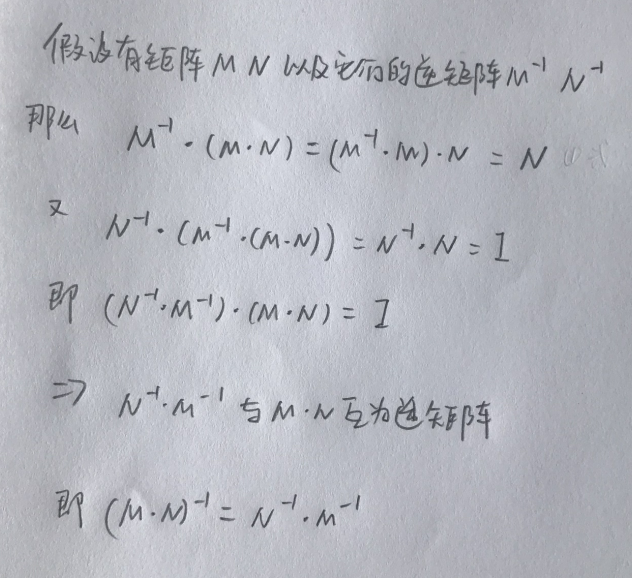线性代数：转置矩阵（matrix transpose）和逆矩阵（matrix inverse）

       这一篇是为了后面着色效果的数学基础做积累，之前我们使用矩阵的大部分情况都是直接的仿射空间变换，就是仿射空间A变换到仿射空间B，使用矩阵也都是如下：

       矩阵T*齐次坐标V = 齐次坐标V’

       其计算细节也就是矩阵行与向量列的点积，其计算意义也就是获得新仿射空间中的坐标分量，也聊了很多了。

       这次我们就来学两个矩阵的操作，一个是矩阵的转置操作（得到转置矩阵），一个是矩阵的逆操作（得到逆矩阵）。

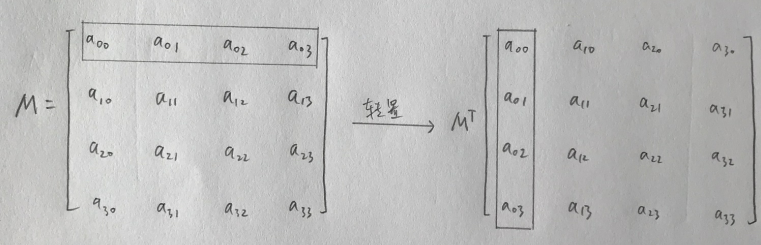
       ①.先看下数学上怎么定义转置矩阵的：

       将矩阵的行列互换得到的新矩阵称为转置矩阵，转置矩阵的行列式不变。

       这里我用4×4矩阵演示一下，因为三维图形开发中使用4×4矩阵。

       同时转置矩阵有以下的运算性质：

       前三个应该不难理解，可能一眼就看出来了，第四个运算性质要稍微演示一下：

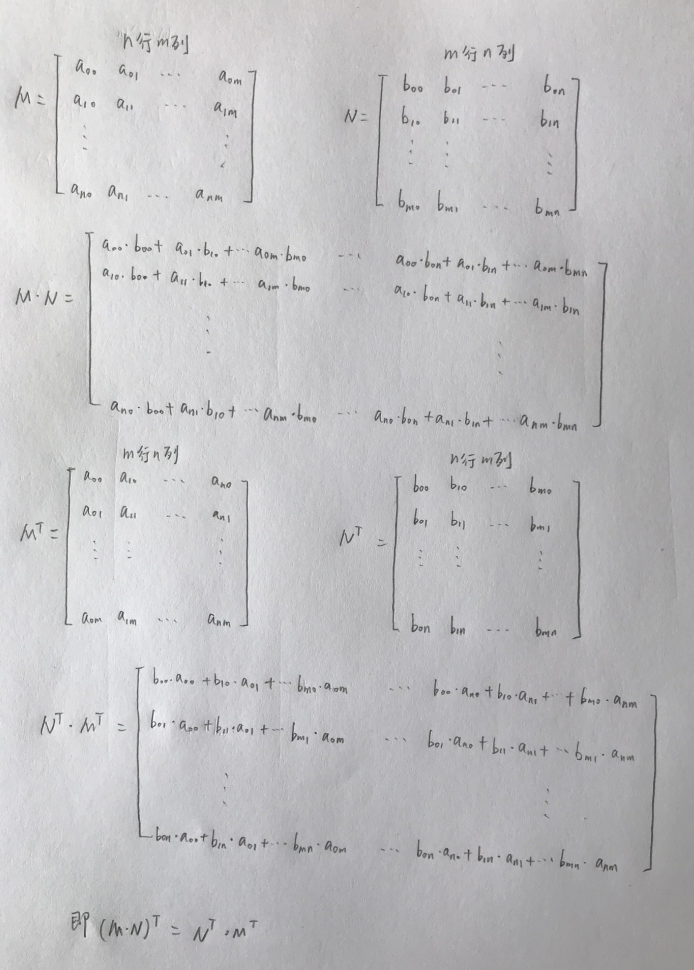
       第四个公式推导，可以用4×4矩阵推算一下，因为我们三维图形学中基本也就只用4×4矩阵了，推导一遍可以加深印象。

       然后将推导过程印在脑海里，后面碰到相关计算就能一目了然了。

       ②再来看看数学上怎么定义逆矩阵的：

       存在矩阵M以及矩阵N，假如M*N = 矩阵I（Identify Matrix单位矩阵），那么矩阵M和矩阵N互为逆矩阵。

       这么一看逆矩阵有个很大的作用就是“还原变换”，什么意思呢，假设M与N互为逆矩阵，那么M·N·齐次坐标A得到的还是原来的齐次坐标A，那么就意味着还原了这个变换，从仿射空间角度来讲就是，仿射空间A经过矩阵M变换到仿射空间B，那么仿射空间B经过M的逆矩阵N变换就还原成了仿射空间A。

       那么逆矩阵又有哪些运算性质呢？如下：

       第一个一目了然了。

       第二个稍微需要描叙一下：

       第三个可能也需要推算一下：

       好，到这里，转置矩阵和逆矩阵的常用公式性质都演示了一遍，顺便说下为什么要观察学习这两个矩阵操作呢？或者说这两个矩阵操作具体有什么用呢？就为了好玩推出一些稀奇古怪的公式定理？nonono，这和后面需要在三维图形学中的特异空间推导有极大关系，这里先提前做好知识储备工作，后面就来上实际的CG shader应用。

       so，我们接下来继续。