向量的点积和叉积_二维a×b叉乘运算公式

1.点积
2.叉积

1.点积:

一个向量在另一个向量上的投影的长度*另一个向量的长度,正负代表方向。

a(x1,y1),b(x2,y2) a,b向量的点积 = x1x2+y1y2。

点积代表的含义为向量a在b上的投影与b长度的乘积(反过来b在a上一样)

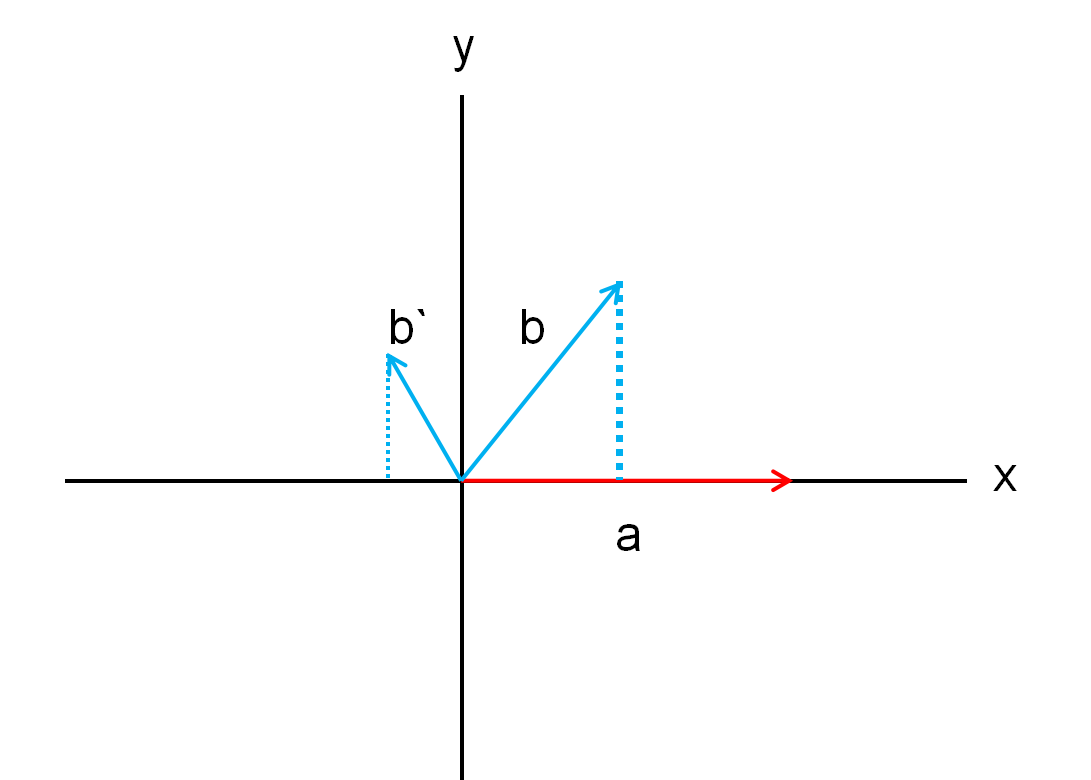
点积大于0的时候代表投影在另一个向量上，也就是说两个向量的角度差不超90

等于0的时候代表90度

小于零代表角度差大于90度

如下图所示,a向量与b向量的点积为正,与b`向量的点积为负。

2.叉积

叉积的概念: 叉积的绝对值代表a,b向量围合起来的四边形的面积,正负表示两个向量相对的位置。

a,b向量的叉积 = x1y2 – y1x2。

叉积的绝对值代表a,b向量围合起来的四边形的面积，而正负代表后一个向量位于前一个向量的什么位置(注意这里和点积有区别，向量相乘的先后对于叉积是有影响的)。

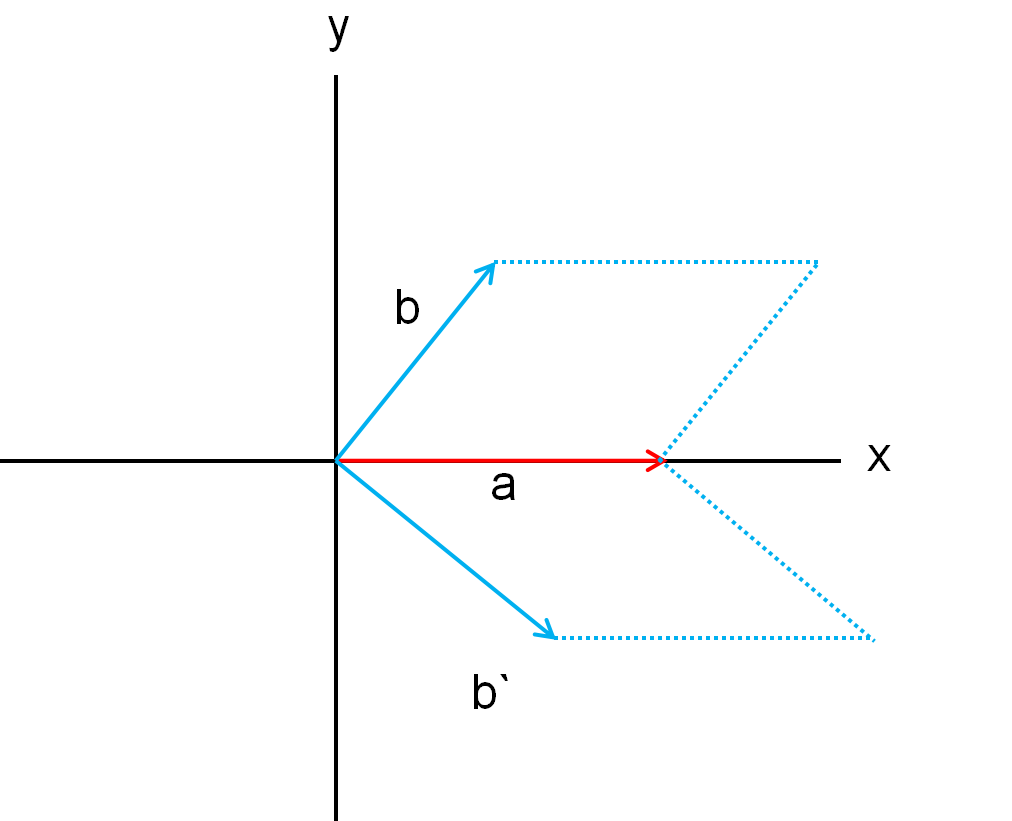
现在a先b后，如果a位于b的顺时针方向(180度内)，那么叉积为正。反之为负，如果共线，则为0。

如下图所示,a向量与b向量的叉积为正,因为a在b的顺时针方向。而a向量与b`的向量的叉积为负。

这些所展示的都是二维空间里的表现形式,其应用可以扩展到多维空间.

今天的文章向量的点积和叉积_二维a×b叉乘运算公式分享到此就结束了，感谢您的阅读。