神经网络学习 之 M-P模型「建议收藏」

M-P模型的来源

所谓M-P模型，其实是按照生物神经元的结构和工作原理构造出来的一个抽象和简化了的模型。
下图是生物神经元结构。

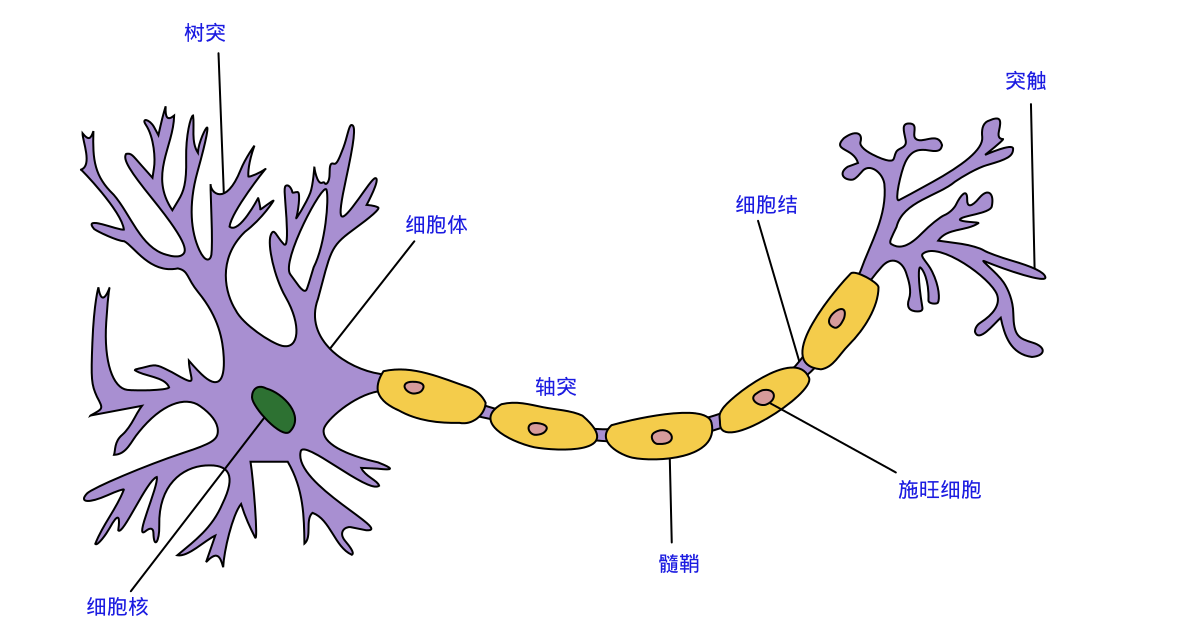
大家可以查一查一些生物方面的书籍，了解一下这个神经元是如何工作的。我们可以概括出生物神经网络的假定特点：

1. 每个神经元都是一个
多输入单输出的信息处理单元；

2. 神经元输入
分兴奋性输入和
抑制性输入两种类型；

3. 神经元具有
空间整合特性和
阈值特性；

4. 神经元输入与输出间有固定的
时滞，主要取决于突触延搁

---

M-P模型

按照生物神经元，我们建立M-P模型。为了使得建模更加简单，以便于进行形式化表达，我们忽略时间整合作用、不应期等复杂因素，并把神经元的突触时延和强度当成常数。下图就是一个M-P模型的示意图。

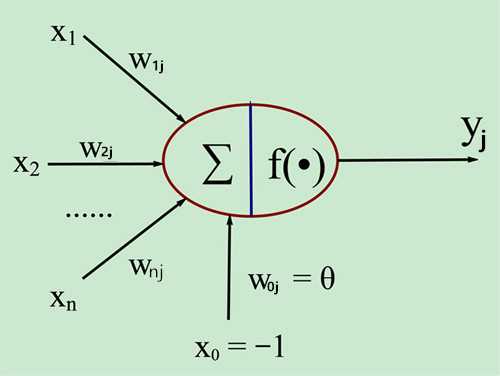
那么接下来就好类比理解了。我们将这个模型和生物神经元的特性列表来比较：






结合M-P模型示意图来看，对于某一个神经元

j
$j$ （注意别混淆成变量了，在这里



j

$j$ 只是起到标识某个神经元的作用），它可能接受同时接受了许多个输入信号，用

χi
$\chi_i$ 表示。

由于生物神经元具有不同的突触性质和突触强度，所以对神经元的影响不同，我们用权值

ωij
$\omega_{ij}$ 来表示，其正负模拟了生物神经元中突出的兴奋和抑制，其大小则代表了突出的不同连接强度。



θj
$\theta_j$表示为一个阈值（threshold），或称为偏置（bias）。

由于累加性，我们对全部输入信号进行累加整合，相当于生物神经元中的膜电位（水的变化总量），其值就为：

$$net′_j(t)=\sum _{i=1}^n\omega_{ij}χ_i(t)-\theta_j$$

神经元激活与否（外接专用水管流出与否）取决于某一阈值电平（水位高度），即只有当其输入总和超过阈值

θj
$\theta_j$ 时，神经元才被激活而发放脉冲，否则神经元不会发生输出信号。整个过程可以用下面这个函数来表示：

$$y_j=f(net_j)$$



yj
$y_j$表示神经元

j
$j$的输出，函数



f

$\cal f$称为激活函数 ( Activation Function )或转移函数 ( Transfer Function ) ，

net‘j(t)
$net′_j(t)$称为净激活(net activation)。

若将阈值看成是神经元

j
$j$的一个输入




今天的文章神经网络学习 之 M-P模型「建议收藏」分享到此就结束了，感谢您的阅读。