music算法doa_cordic算法原理与实现

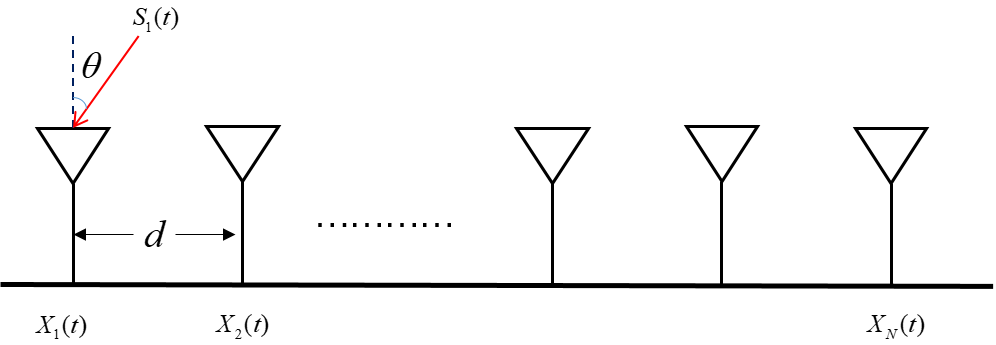
DOA估计算法

DOA（Direction Of Arrival）波达方向定位技术主要有ARMA谱分析、最大似然法、熵谱分析法和特征分解法，特征分解法主要有MUSIC算法、ESPRIT算法WSF算法等。
MUSIC (Multiple Signal Classification)算法，即多信号分类算法，由Schmidt等人于1979年提出。MUSIC算法是一种基于子空间分解的算法，它利用信号子空间和噪声子空间的正交性，构建空间谱函数，通过谱峰搜索，估计信号的参数。对于声源定位来说，需要估计信号的DOA。MUSIC算法对DOA的估计有很高的分辨率，且对麦克风阵列的形状没有特殊要求，因此应用十分广泛。

运用矩阵的定义，可得到更为简洁的表达式：

$X=AS+N$

式中

$X=[x_1(t),x_2(t),...x_M(t){]}^T$，
$S=[S_1(t),S_2(t),...S_D(t){]}^T$，
$A=[a({\theta }_1),a({\theta }_2),...a({\theta }_D){]}^T$，
$N=[n_1(t),n_2(t),...n_M(t){]}^T$。

$X$为阵元的输出，$A$为方向响应向量，$S$是入射信号，$N$表示阵列噪声。

其中 ${\phi }_k=\frac{2\pi d}{\lambda }sin{\theta }_k$有

$$A=[a({\theta }_1),a({\theta }_2),...a({\theta }_D){]}^T=\left[\begin{array}{cccc}1& 1& \cdots & 1\\ e^{-j{\phi }_1}& e^{-j{\phi }_2}& \cdots & e^{-j{\phi }_D}\\ ⋮& ⋮& \ddots & ⋮\\ e^{-j(M-1){\phi }_1}& e^{-j(M-1){\phi }_2}& \cdots & e^{-j(M-1){\phi }_D}\end{array}\right]$$
对$x_m(t)$进行N点采样，要处理的问题就变成了通过输出信号$x_m(t)$的采样 { x m ( i ) = 1 , 2 , . . . , M } \{ x_m (i)=1,2,…,M\} {
xm​(i)=1,2,...,M}估计信号源的波达方向角${\theta }_1,{\theta }_2...{\theta }_D$,由此可以很自然的将阵列信号看作是噪声干扰的若干空间谐波的叠加，从而将波达方向估计问题与谱估计联系起来。
对阵列输出X做相关处理，得到其协方差矩阵

$R_x=E[X{X}^H]$

其中$H$表示矩阵的共轭转置。
根据已假设信号与噪声互不相关、噪声为零均值白噪声，因此可得到：

$R_x=E[(AS+N)(AS+N{)}^H]=AE[S{S}^H]A^H+E[N{N}^H]=A{R}_S{A}^H+R_N$
其中$R_s=E[S{S}^H]$称为信号相关矩阵

$R_N={\sigma }^{2}I$是噪声相关阵

${\sigma }^2$是噪声功率

$I$是$M\times M$阶的单位矩阵

在实际应用中通常无法直接得到$R_x$，能使用的只有样本的协方差矩阵：
$\widehat{R_x}=\frac{1}{N}{\sum }_{i=1}^{N}X(i)X^H(i)$，$\widehat{R_x}$是$R_x$的最大似然估计。

当采样数$N\to \infty$，他们是一致的，但实际情况将由于样本数有限而造成误差。根据矩阵特征分解的理论，可对阵列协方差矩阵进行特征分解，首先考虑理想情况，即无噪声的情况：$R_x=A{R}_s{A}^H$，对均匀线阵，矩阵A由
$$A=[a({\theta }_1),a({\theta }_2),...a({\theta }_D){]}^T=\left[\begin{array}{cccc}1& 1& \cdots & 1\\ e^{-j{\phi }_1}& e^{-j{\phi }_2}& \cdots & e^{-j{\phi }_D}\\ ⋮& ⋮& \ddots & ⋮\\ e^{-j(M-1){\phi }_1}& e^{-j(M-1){\phi }_2}& \cdots & e^{-j(M-1){\phi }_D}\end{array}\right]$$
所定义的范德蒙德矩阵，只要满足${\theta }_i\ne {\theta }_j,i\ne j$，则他的各列相互独立。

若$R_s$为非奇异矩阵$Rank(R_s)=D$，各信号源两两不相干，且$M>D$，则$rand(A{R}_s{A}^H)=D$，

由于$R_x=E[X{X}^H]$，有：

$R_s^H=R_x$

即$R_s$为Hermite矩阵，它的特性是都是实数，又由于$R_s$为正定的，因此$A{R}_{s}A\dots \dots H$为半正定的，它有D个正特征值和$M-D$个零特征值。

再考虑有噪声存在的情况

$R_x=A{R}_s{A}^H+{\sigma }^{2}I$

由于${\sigma }^2>0$，$R_x$为满秩阵，所以$R_x$有M个正实特征值${\lambda }_1,{\lambda }_2...{\lambda }_M$

分别对应于M个特征向量$v_1,v_2...v_M$。又由于$R_x$为Hermite矩阵，所以各特征向量是正交的，即：$v_i^H{v}_j=0,i\ne j$与信号有关的特征值只有D个,分别等于矩阵$A{R}_s{A}^H$的各特征值与${\sigma }^2$之和，其余$M-D$个特征值为${\sigma }^2$，即${\sigma }^2$为$R$的最小特征值，它是$M-D$维的，对应的特征向量$v_i,i=1,2,...,M$中，也有D个是与信号有关的，另外$M-D$个是与噪声有关的，可利用特征分解的性质求出信号源的波达方向${\theta }_k$。

MUSIC算法的原理及实现

通过对协方差矩阵的特征值分解，可得到如下结论：

将矩阵$R_x$的特征值进行从小到大的排序，即${\lambda }_1\ge {\lambda }_2\ge ...\ge {\lambda }_M>0$，其中D个较大的特征值对应于信号，$M-D$个较小的特征值对应于噪声。

矩阵$R_x$的属于这些特征值的特征向量也分别对应于各个信号和噪声，因此可把$R_x$的特征值（特征向量）划分为信号特征（特征向量）与噪声特征（特征向量）。

设${\lambda }_i$为$R_x$的第$i$个特征值，$v_i$是与${\lambda }_i$个相对应的特征向量，有：

$R_x{v}_i={\lambda }_i{v}_i$

再设${\lambda }_i={\sigma }^2$是$R_x$的最小特征值$R_x{v}_i={\sigma }^2{v}_{i}i=D+1,D+2...M$，

将$R_x=A{R}_s{A}^H+{\sigma }^{2}I$代入可得${\sigma }^2{v}_i=(A{R}_s{A}^H+{\sigma }^{2}I)v_i$，

将其右边展开与左边比较得：

$A{R}_s{A}^H{v}_i=0$

因$A^{H}A$是$D\ast D$维的满秩矩阵，$(A^{H}A{)}^{-1}$存在；

而$R_s^{-1}$同样存在，则上式两边同乘以$R_s^{-1}(A^{H}A{)}^{-1}{A}^H$，

有：

$R_s^{-1}(A^{H}A{)}^{-1}{A}^{H}A{R}_s{A}^H{v}_i=0$

于是有

$A^H{v}_i=0，i=D+1,D+2,...,M$

上式表明：噪声特征值所对应的特征向量（称为噪声特征向量）$v_i$，与矩阵$A$的列向量正交，而$A$的各列是与信号源的方向相对应的，这就是利用噪声特征向量求解信号源方向的出发点。

用各噪声特征向量为例，构造一个噪声矩阵$E_n$:

$E_n=[v_{D+1},v_{D+2},...v_M]$

定义空间谱$P_{mu}(\theta )$:

$P_{mu}(\theta )=\frac{1}{a^H(\theta )}{E}_n{E}_n^{H}a(\theta )=\frac{1}{\Vert E_n^{H}a(\theta ){\Vert }^2}$

该式中分母是信号向量和噪声矩阵的内积，当$a(\theta )$和$E_n$的各列正交时，该分母为零，但由于噪声的存在，它实际上为一最小值，因此$P_{mu}(\theta )$有一尖峰值，由该式，使$\theta$变化，通过寻找波峰来估计到达角。

MUSIC算法实现的步骤

1.根据N个接收信号矢量得到下面协方差矩阵的估计值：

$R_x=\frac{1}{N}{\sum }_{i=1}^{N}X(i)X^H(i)$

对上面得到的协方差矩阵进行特征分解

$R_x=A{R}_s{A}^H+{\sigma }^{2}I$

2.按特征值的大小排序将与信号个数$D$相等的特征值和对应的特征向量看做信号部分空间，将剩下的$M-D$个特征值和特征向量看做噪声部分空间，得到噪声矩阵$E_n$:

$A^H{v}_i=0，i=D+1,D+2,...,M$

$E_n=[v_{D+1},v_{D+2},...v_M]$

3.使$\theta$变化，按照式

$P_{mu}(\theta )=\frac{1}{a^H(\theta )E_n{E}_n^{H}a(\theta )}$

来计算谱函数，通过寻求峰值来得到波达方向的估计值。

clear; close all;
%%%%%%%% MUSIC for Uniform Linear Array%%%%%%%%
derad = pi/180;      %角度->弧度
N = 8;               % 阵元个数        
M = 3;               % 信源数目
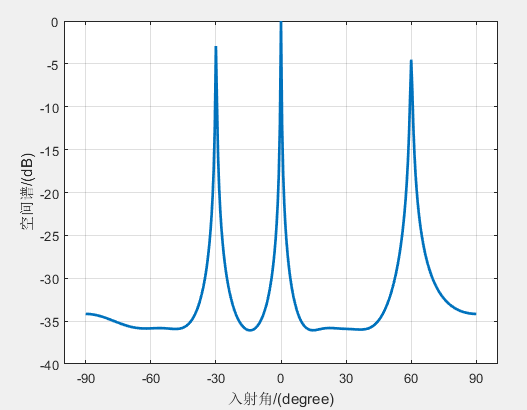
theta = [-30 0 60];  % 待估计角度
snr = 10;            % 信噪比
K = 512;             % 快拍数
 
dd = 0.5;            % 阵元间距 
d=0:dd:(N-1)*dd;
A=exp(-1i*2*pi*d.'*sin(theta*derad));  %方向矢量

%%%%构建信号模型%%%%%
S=randn(M,K);             %信源信号，入射信号
X=A*S;                    %构造接收信号
X1=awgn(X,snr,'measured'); %将白色高斯噪声添加到信号中
% 计算协方差矩阵
Rxx=X1*X1'/K;
% 特征值分解
[EV,D]=eig(Rxx);                   %特征值分解
EVA=diag(D)';                      %将特征值矩阵对角线提取并转为一行
[EVA,I]=sort(EVA);                 %将特征值排序 从小到大
EV=fliplr(EV(:,I));                % 对应特征矢量排序
                 
 
% 遍历每个角度，计算空间谱
for iang = 1:361
    angle(iang)=(iang-181)/2;
    phim=derad*angle(iang);
    a=exp(-1i*2*pi*d*sin(phim)).'; 
    En=EV(:,M+1:N);                   % 取矩阵的第M+1到N列组成噪声子空间
    Pmusic(iang)=1/(a'*En*En'*a);
end
Pmusic=abs(Pmusic);
Pmmax=max(Pmusic)
Pmusic=10*log10(Pmusic/Pmmax);            % 归一化处理
h=plot(angle,Pmusic);
set(h,'Linewidth',2);
xlabel('入射角/(degree)');
ylabel('空间谱/(dB)');
set(gca, 'XTick',[-90:30:90]);
grid on;

实现结果

今天的文章music算法doa_cordic算法原理与实现分享到此就结束了，感谢您的阅读。