数据结构与算法之Huffman tree(赫夫曼树 / 霍夫曼树 / 哈夫曼树 / 最优二叉树)

赫夫曼树概述

HuffmanTree因为翻译不同所以有其他的名字：赫夫曼树、霍夫曼树、哈夫曼树

赫夫曼树又称最优二叉树，是一种带权路径长度最短的二叉树。所谓树的带权路径长度，就是树中所有的叶结点的权值乘上其到根结点的路径长度（若根结点为0层，叶结点到根结点的路径长度为叶结点的层数）。树的路径长度是从树根到每一结点的路径长度之和，记为WPL=（W1L1+W2L2+W3L3+…+WnLn），N个权值Wi（i=1,2,…n）构成一棵有N个叶结点的二叉树，相应的叶结点的路径长度为Li（i=1,2,…n）。可以证明赫夫曼树的WPL是最小的。

定义

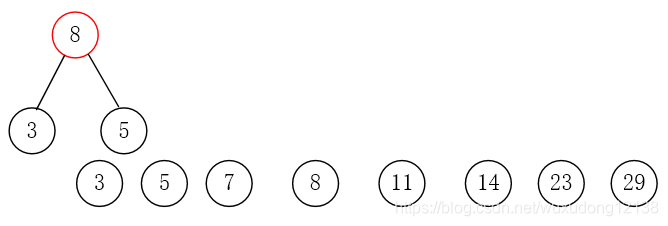
路径： 路径是指从一个节点到另一个节点的分支序列。

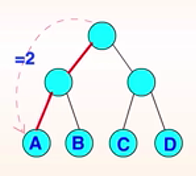
路径长度： 指从一个节点到另一个结点所经过的分支数目。 如下图：从根节点到a的分支数目为2

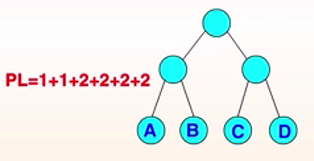
树的路径长度： 树中所有结点的路径长度之和为树的路径长度PL。 如下图：PL为10

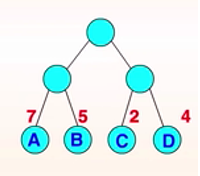
节点的权： 给树的每个结点赋予一个具有某种实际意义的实数，我们称该实数为这个结点的权。如下图：7、5、2、4

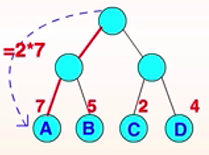
带权路径长度： 从树根到某一结点的路径长度与该节点的权的乘积，叫做该结点的带权路径长度。如下图：A的带权路径长度为2*7=14

树的带权路径长度（WPL）： 树的带权路径长度为树中所有叶子节点的带权路径长度之和

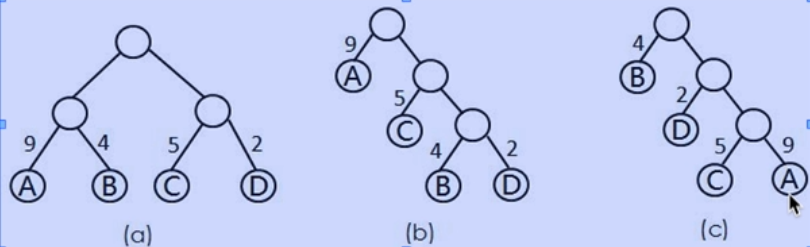
最优二叉树：权值最大的节点离跟节点越近的二叉树，所得WPL值最小，就是最优二叉树。如下图：（b）

• （a）WPL=9*2+4*2+5*2+2*2=40
• （b）WPL=9*1+5*2+4*3+2*3=37
• （c） WPL=4*1+2*2+5*3+9*3=50

构造赫夫曼树步骤

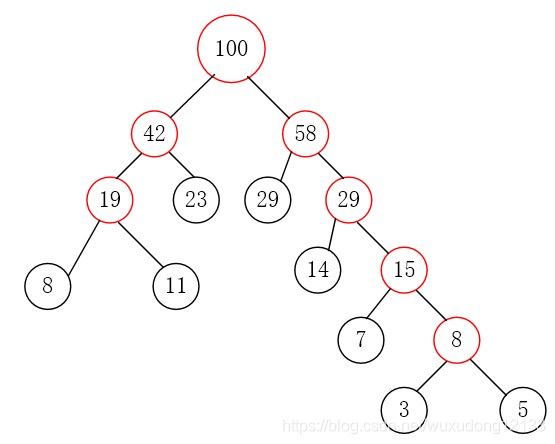
对于数组{5,29,7,8,14,23,3,11}，我们把它构造成赫夫曼树

第一步：使用数组中所有元素创建若干个二叉树，这些值作为节点的权值（只有一个节点）。

第二步：将这些节点按照权值的大小进行排序。

第三步：取出权值最小的两个节点，并创建一个新的节点作为这两个节点的父节点，这个父节点的权值为两个子节点的权值之和。将这两个节点分别赋给父节点的左右节点

第四步：删除这两个节点，将父节点添加进集合里

第五步：重复第二步到第四步，直到集合中只剩一个元素，结束循环

代码实现

• 节点类

//接口实现排序功能
public class Node implements Comparable<Node> { 
   
    int value;
    Node left;
    Node right;

    public Node(int value) { 
   
        this.value = value;
    }

    @Override
    public int compareTo(Node o) { 
   
        return -(this.value - o.value); //集合倒叙，从大到小
    }

    @Override
    public String toString() { 
   
        return "Node value=" + value ;
    }
}

• 测试类

import java.util.ArrayList;
import java.util.Collections;
import java.util.List;

public class Demo { 
   
    public static void main(String[] args) { 
   
        int[] arr = { 
   5, 29, 7, 8, 14, 23, 3, 11};
        Node node = createHuffmanTree(arr);
        System.out.println(node); //Node value=100
    }

    //创建赫夫曼树
    public static Node createHuffmanTree(int[] arr) { 
   
        //使用数组中所有元素创建若干个二叉树（只有一个节点）
        List<Node> nodes = new ArrayList<>();
        for (int value : arr) { 
   
            nodes.add(new Node(value));
        }

        //循环处理
        while (nodes.size() > 1) { 
   
            //排序
            Collections.sort(nodes);
            //取出最小的两个二叉树（集合为倒叙，从大到小）
            Node left = nodes.get(nodes.size() - 1); //权值最小
            Node right = nodes.get(nodes.size() - 2); //权值次小
            //创建一个新的二叉树
            Node parent = new Node(left.value + right.value);
            //删除原来的两个节点
            nodes.remove(left);
            nodes.remove(right);
            //新的二叉树放入原来的二叉树集合中
            nodes.add(parent);
            //打印结果
            System.out.println(nodes);
        }
        return nodes.get(0);
    }
}

• 循环次数结果

[Node value=29, Node value=23, Node value=14, Node value=11, Node value=8, Node value=7, Node value=8]
[Node value=29, Node value=23, Node value=14, Node value=11, Node value=8, Node value=15]
[Node value=29, Node value=23, Node value=15, Node value=14, Node value=19]
[Node value=29, Node value=23, Node value=19, Node value=29]
[Node value=29, Node value=29, Node value=42]
[Node value=42, Node value=58]
[Node value=100]
Node value=100

Process finished with exit code 0

今天的文章数据结构与算法之Huffman tree(赫夫曼树 / 霍夫曼树 / 哈夫曼树 / 最优二叉树)分享到此就结束了，感谢您的阅读。