关于Kappa系数、二次加权Kappa系数
Kappa系数
1. 定义
kappa系数是统计学中度量一致性的指标, 值在[-1,1]。对于评分系统, 一致性就是不同打分人平均的一致性; 对于分类问题,一致性就是模型预测结果和实际分类结果是否一致。
kappa系数的计算是基于混淆矩阵, 取值为-1到1之间, 通常大于0。
基于混淆矩阵的Kappa系数计算公式如下:
k a p p a = p o − p e 1 − p e \large kappa=\frac{p_o-p_e}{1-p_e} kappa=1−pepo−pe
其中:
p o p_o po为预测的准确率,也可理解为预测的一致性 p o = 对角线元素之和 整个矩阵的元素之和 \large p_o=\frac{对角线元素之和}{整个矩阵的元素之和} po=整个矩阵的元素之和对角线元素之和,也就是ACC。
p e p_e pe表示偶然一致性, p e = ∑ i 第 i 行元素之和 × 第 i 列元素之和 ( ∑ 矩阵所有元素 ) 2 p_e=\frac{\sum_i第i行元素之和\times第i列元素之和}{\rm(\sum矩阵所有元素)^2} pe=(∑矩阵所有元素)2∑i第i行元素之和×第i列元素之和,也就是所有类别分别对应“实际与预测数量的乘积”总和除以“样本总数的平方”。
kappa值含义:
-1:完全不一致
0: 偶然一致
0.0~0.20: 极低的一致性(slight)
0.21~0.40: 一般的一致性(fair)
0.41~0.60: 中等的一致性(moderate)
0.61~0.80: 高度的一致性(substantial)
0.81~1: 几乎完全一致(almost perfect)
2. 使用Kappa的原因
分类问题中,最常见的评价指标是acc,它能够直接反映分正确的比例,同时计算非常简单。但是实际的分类问题中,各个类别的样本数量往往不太平衡。在这种不平衡数据集上如不加以调整,模型很容易偏向大类别而放弃小类别(eg: 正负样本比例1:9,直接全部预测为负,acc也有90%。但正样本就完全被“抛弃”了)。此时整体acc挺高,但是部分类别完全不能被召回。
这时需要一种能够惩罚模型的“偏向性”的指标来代替acc。而根据kappa的计算公式,越不平衡的混淆矩阵, p e p_e pe越高,kappa值就越低,正好能够给“偏向性”强的模型打低分。
Kappa系数计算示例
混淆矩阵:
| 成绩评级 | 好 | 中 | 差 |
|---|---|---|---|
| 好 | a | b | c |
| 中 | d | e | f |
| 差 | g | h | i |
p o = a + e + i a + b + c + d + e + f + g + h + i p_o=\frac{a+e+i}{a+b+c+d+e+f+g+h+i} po=a+b+c+d+e+f+g+h+ia+e+i
p e = ( a + d + g ) × ( a + b + c ) + ( d + e + f ) × ( b + e + h ) + ( c + f + i ) × ( g + h + i ) ( a + b + c + d + e + f + g + h + i ) 2 p_e=\frac{(a+d+g)\times(a+b+c)+(d+e+f)\times(b+e+h)+(c+f+i)\times(g+h+i)}{(a+b+c+d+e+f+g+h+i)^2} pe=(a+b+c+d+e+f+g+h+i)2(a+d+g)×(a+b+c)+(d+e+f)×(b+e+h)+(c+f+i)×(g+h+i)
将得到的 p o p_o po和 p e p_e pe带入Kappa计算公式即可。
二次加权Kappa(Quadratic Weighted Kappa——QWK)
对于一些有序关系的级别得分, 使用上面简单的计算方法存在一些问题。 比如在疾病预判时, 假设病人是无病的, 一个医生预测为得病且特别严重, 另一个医生预测为得病且中度. 很明显, 第一个医生的预测结果更加不可接受。 所以, 我们要在计算kappa值时加入权重的概念, 以区分这种预测结果的后果程度。
其中, w i , j w_{i,j} wi,j是平方加权, O i , j O_{i,j} Oi,j为观察矩阵中的元素, E i , j E_{i,j} Ei,j为期望矩阵中的元素,N为分类的总类数,二次加权Kappa的数学计算公式为:
k = 1 − ∑ i , j w i , j O i , j ∑ i , j w i , j E i , j w i , j = ( i − j ) 2 ( N − 1 ) 2 E i , j = ( x × y ) n × m k=1-\frac{\sum_{i,j}w_{i,j}O_{i,j}}{\sum_{i,j}w_{i,j}E_{i,j}} \\ w_{i,j}=\frac{(i-j)^2}{(N-1)^2}\\ E_{i,j}=\frac{(x\times y)}{n\times m} k=1−∑i,jwi,jEi,j∑i,jwi,jOi,jwi,j=(N−1)2(i−j)2Ei,j=n×m(x×y)
【注】 E i , j E_{i,j} Ei,j为自己写出的公式,根据参考资料的文字描述得出。
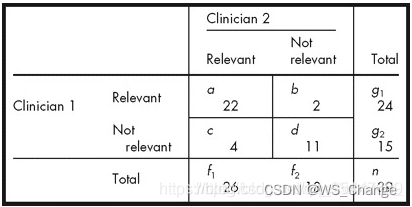
上面的公式当中的i和j,代表的是矩阵中元素所在位置的行数和列数,如下表中的a对应的i=1,j=1,以此类推。而 x x x代表元素所在行的元素之和, y y y代表元素所在列的元素之和, n n n代表该矩阵的行的元素总数, m m m代表该矩阵的列的元素总数。网上很多帖子都没有说清楚公式中字母的含义,导致初期看的很困惑,下面举个很“常见”的例子:
这里的N=2,i=j=2。
完整的计算公式应该如下:
∑ i , j w i , j O i , j = ( 1 − 1 ) 2 ( 2 − 1 ) 2 × 22 + ( 1 − 2 ) 2 ( 2 − 1 ) 2 × 2 + ( 2 − 1 ) 2 ( 2 − 1 ) 2 × 4 + ( 2 − 2 ) 2 ( 2 − 1 ) 2 × 11 = 0 × 22 + 1 × 2 + 1 × 4 + 0 × 11 = 6 \sum_{i,j}w_{i,j}O_{i,j}=\frac{(1-1)^2}{(2-1)^2}\times22+\frac{(1-2)^2}{(2-1)^2}\times2+\frac{(2-1)^2}{(2-1)^2}\times4+\frac{(2-2)^2}{(2-1)^2}\times11\\=0\times22+1\times2+1\times4+0\times11=6 i,j∑wi,jOi,j=(2−1)2(1−1)2×22+(2−1)2(1−2)2×2+(2−1)2(2−1)2×4+(2−1)2(2−2)2×11=0×22+1×2+1×4+0×11=6
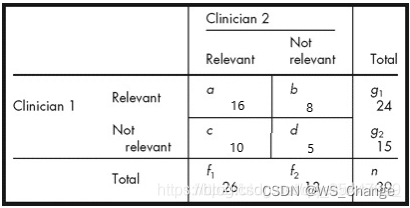
根据该表我们还可以算出他的期望矩阵 E E E,如下表所示:
以表格中a为例, E 1 , 1 = ( 24 × 26 ) 39 = 16 E_{1,1}=\large\frac{(24\times26)}{39}=16 E1,1=39(24×26)=16,其他元素以此类推。
∑ i , j w i , j E i , j = ( 1 − 1 ) 2 ( 2 − 1 ) 2 × ( 24 × 26 ) 39 + ( 1 − 2 ) 2 ( 2 − 1 ) 2 × ( 24 × 13 ) 39 + ( 2 − 1 ) 2 ( 2 − 1 ) 2 × ( 15 × 26 ) 39 + ( 2 − 2 ) 2 ( 2 − 1 ) 2 × ( 15 × 13 ) 39 = 0 × 16 + 1 × 8 + 1 × 10 + 0 × 5 = 18 \sum_{i,j}w_{i,j}E_{i,j}=\frac{(1-1)^2}{(2-1)^2}\times\frac{(24\times26)}{39}+\frac{(1-2)^2}{(2-1)^2}\times\frac{(24\times13)}{39}+\frac{(2-1)^2}{(2-1)^2}\times\frac{(15\times26)}{39}+\frac{(2-2)^2}{(2-1)^2}\times\frac{(15\times13)}{39}\\ =0\times16+1\times8+1\times10+0\times5=18 i,j∑wi,jEi,j=(2−1)2(1−1)2×39(24×26)+(2−1)2(1−2)2×39(24×13)+(2−1)2(2−1)2×39(15×26)+(2−1)2(2−2)2×39(15×13)=0×16+1×8+1×10+0×5=18
所以最终的二次加权Kappa系数就等于 k = 1 − 6 18 = 0.67 k=1-{\large\frac{6}{18}}=0.67 k=1−186=0.67
来源:
二次加权kappa计算公式
kappa与quadratic weighted kappa
今天的文章
【深度学习】关于Kappa系数、二次加权Kappa系数(QWK)分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/80952.html