感兴趣的话大家可以关注一下公众号 : 猿人刘先生 , 欢迎大家一起学习 , 一起进步 , 一起来交流吧!
在计算机中,数据元素并不是孤立、杂乱无序的,而是具有内在联系的数据集合。数据元素之间存在一种或多种特定关系,也就是数据的组织形式。为编写出一个 好”的程序,必须分析待处理对象的特性及各处理对象之间存在的关系。这也就是研究数据结构的意义所在。
1. 数据结构
数据结构是计算机存储、组织数据的方式 , 是相互存在一种或多种特定关系的数据元素的集合 , 按照视点不同 , 我们大概可以把数据结构分为两种 : 物理结构和逻辑结构.
1.1 逻辑结构
指反映数据元素之间的逻辑关系的数据结构 , 其中的逻辑关系是指数据元素之间的前后关系 , 而与它们在计算机中存储位置无关
集合 : 数据结构中的元素除了”同属一个集合的关系”之外 , 别无其他关系
线性结构 : 数据结构中的元素存在一对一的关系
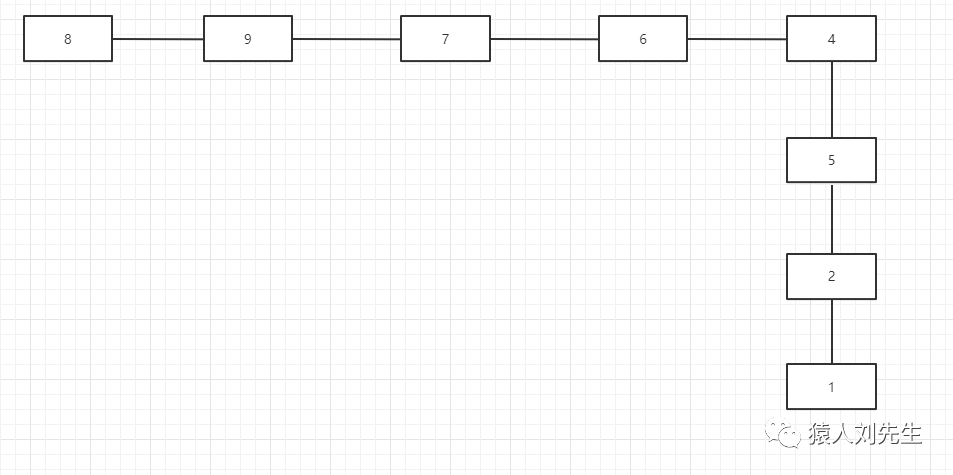
树形结构 : 数据结构中的元素存在一对多的相互关系
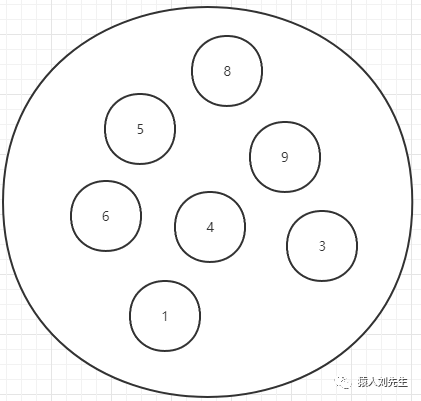
圆形结构 : 数据结构中的元素存在多对多的相互关系
1.2 物理结构
物理结构也叫存储结构 , 指的是数据的逻辑结构在计算机中的存储形式 , 数据是数据元素的集合,那么根据物理结构的定义,实际上就是如何把数据元素存储到计算机的存储器中。存储器主要是针对内存而言的,像硬盘、软盘、光盘等外部存储器的数据组织通常用文件结构来描述
数据的存储结构应正确反映数据元素之间的逻辑关系,这才是最为关键的,如何存储数据元素之间的逻辑关系,是实现物理结构的重点和难点。
数据元素的存储结构形式有两种:顺序存储和链式存储。
顺序存储结构 : 是把数据元素存放在地址连续的存储单元里,其数据间的逻辑关系和物理关系是一致的
链式存储结构 : 是把数据元素存放在任意的存储单元里,这组存储单元可以是连续的,也可以是不连续的 数据元素的存储关系并不能反映其逻辑关系,因此需要用一个指针存放数据元素的地址,这样通过地址就可以找到相关联数据元素的位置 , 显然,链式存储就灵活多了,数据存在哪里不重要,只要有一个指针存放了相应的地址就能找到白了
1.3 数组
数组站在物理结构来说属于顺序结构 , 而站在逻辑结构来说属于线性结构 , 数组是在内存中连续存储的具有相同类型的一组数据的集合 , 在JVM中有堆和栈 , 连续存储指的就是数组中的数据在堆中是连续的排在一起的 , 这就是数组在内存中的一个表现形式
1.3.1 数组的查询
数组的查询是通过一个公式来计算的 :a[n] = 起始地址 + (n * 字节数) , n表示的就是下标 , 比如我们此时要寻找下边为2的元素 , 那么通过公式计算 , 100 + (2*4) , 那么找到的就是地址为108的元素 , 也就是说5 , 因为它有一个公式 , 经过计算 , 可以很快的找到这个元素的地址 , 所以它的查询的时间复杂度是o(1) , 这种情况是根据下标查找 , 也叫随机访问
-
数组支持随机访问,根据下标随机访问的时间复杂度为O(1)
-
数组排好序的前提下 , 使用二分查找的情况 , 数组的时间复杂度为O(logn)
-
数组在顺序查找的情况下 , 需要遍历每一个元素 , 直到相等 , 然后返回 , 所以时间复杂度是O(N)
1.3.2 数组的增加
-
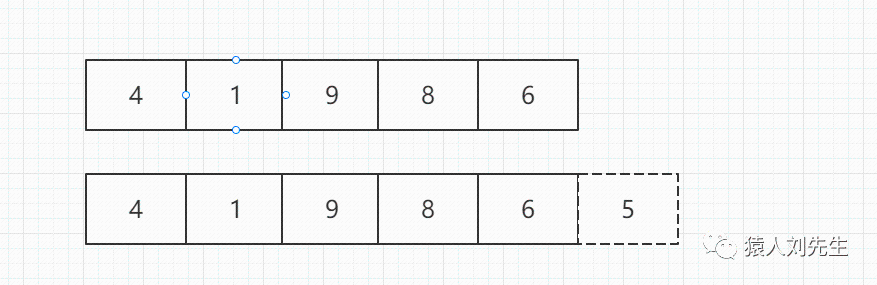
如果使用尾插法 , 时间复杂度为O(1) , 因为不涉及其他元素的移动
-
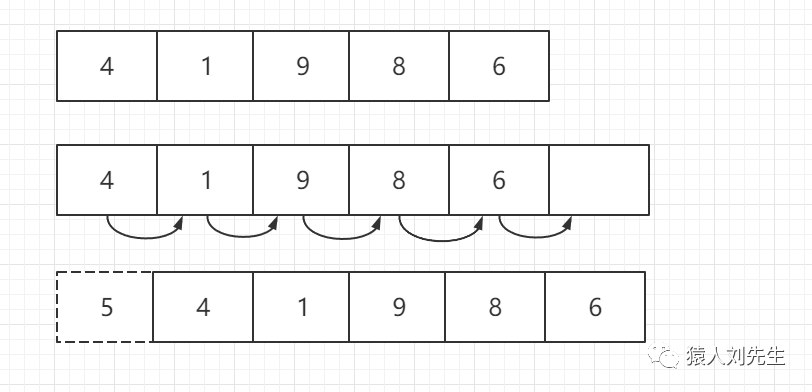
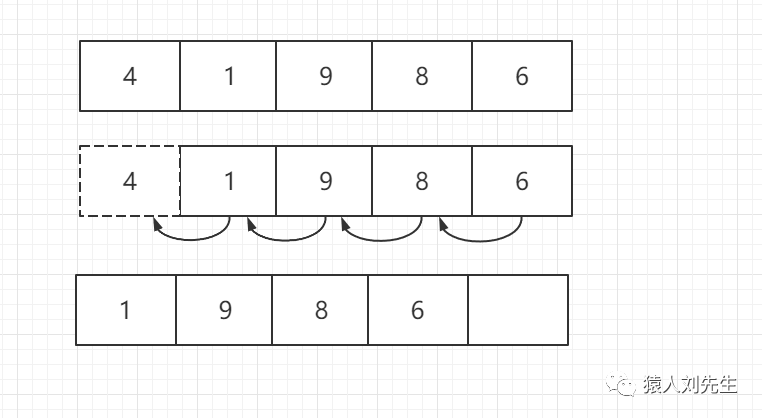
如果使用头插法 , 时间复杂度为O(N) , 因为数组的每一个元素都要向后移动
-
如果在中间插入 , 时间复杂度也是O(N) , 因为插入位置后面的元素也需要向后移动
1.3.3 数组的删除
-
如果使用头删法 , 时间复杂度为O(N) , 因为其它元素要向前移动一位
-
如果使用尾删法 , 时间复杂为O(1) , 不涉及到其它元素的移动
-
如果在中间删除 , 时间复杂度也为O(N) , 因为删除位置之后的元素要向前移动一位
1.4 动态数组
上文我们所分析的数组是常态数组 , 一维数组 , 接下来我们分析动态数组
动态数组(也称为可增数组、可变长数组、动态表、数组表)是一种可随机存取且可自动调整大小的线性数据结构,能够添加或删除元素。
实现动态数组的一个简单方法是,首先初始化固定大小的数组。一旦数组存储满了,创建一个1.5倍于原始数组大小的新数组(将旧数组数据复制进新数组)。同样,若数组中存储的元素个数小于数组大小的一半,则把数组大小减少一半。
1.4.1 动态数组增加
-
动态数组头插时间复杂度O(N) , 因为会涉及到其他元素向后移动或者是扩容
-
动态数组尾插时间复杂度如果不扩容 , 那么是O(1) , 如果需要扩容的话 , 那么就是O(N)
-
动态数组中间插入 , 时间复杂度O(N) , 因为会涉及其它元素的移动或者是数组的扩容
1.4.2 动态数组删除
-
动态数组头删时间复杂度 : O(N) . 因为会涉及其他元素向前移动或者是缩容的情况
-
动态数组尾删时间复杂度 , 如果考虑缩容 , 那么时间复杂度为O(N) , 否则的话时间复杂度为O(1)
-
动态数组中间删除时间复杂度为O(N) , 因为会涉及到其他元素向前移动或者是缩容
1.4.3 动态数组的查询
- 动态数组查询的情况和常态数组是相同的
1.4.4 动态数组的扩容
当添加元素时,旧数组容量不够了,这时候不能直接给旧数组扩容,因为旧数组的容量在创建的时候就确定好了 , 所以需要创建一个新的数组,并把旧数组的的元素挪到新的数组中
步骤如下:
-
判断容量是否够用,也就是size + 1 <= elements.length;elements表示旧数组
-
创建一个新的数组newElements,容量为elements的1.5倍(使用位运算效率更高);
-
将elements中的元素挪到newElements中;
-
将element指针指向newElements;
1.4.5 动态数组的缩容
当删除元素时,旧数组中元素会越来越少,当少到一定程度时,数组原有开辟的空间就会浪费,所以就要考虑到缩容操作 , 所以和扩容一样,需要创建一个新的数组,并将旧数组中的元素挪到新的数组中;
步骤如下:
-
判断容量是否够用,也就是size 大于elements容量的一半时,或者容量小于DEFAULIT_CAPACITY默认容量10时,没必要进行缩容操作;
-
创建一个新的数组newElements,容量为elements的1/2(使用位运算效率更高);
-
将elements中的元素挪到newElements中;
-
将element指针指向newElements;
1.5 链表
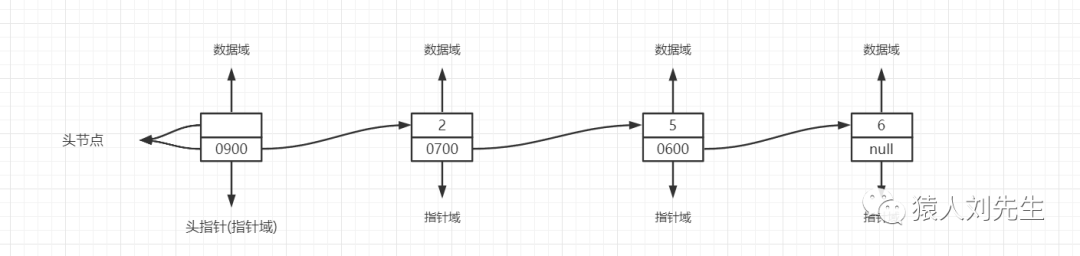
链表站在物理结构来说属于链式结构 , 而站在逻辑结构来说也属于线性结构 , 链表包含单链表,双向链表,循环链表等等。相对于线性表,添加,删除操作非常方便,因为不用移动大量的结点,只需要修改对应的前后结点指针即可,既然是链表,结点除了基本信息也要加入下一结点指针,方便计算机在内存中查找 , 我们通常把存放基本信息的域成为数据域 , 存放直接后继位置的域成为指针域 , 这两部分组成的数据元素的存储映象 , 称为结点 , 第一个结点称为头结点也叫哑元结点 , 第二个结点才属于真正的第一结点 , 而头结点的数据域可以不存放任何东西 , 也可以存放链表的长度等一些公共的信息
1.5.1 单链表
单链表中包含多个节点 , 每一个结点都有一个指向后继元素的next(下一个)指针 , 最后一个结点的next指针值为null , 表示该链表的结束
1.5.2 循环链表
将单链表中终端结点的指针端自空指针改为指向头结点,就使整个单链表形成个环,这种头尾相接的单链表称 单循环链表,简称循环链表
1.5.3 双向链表
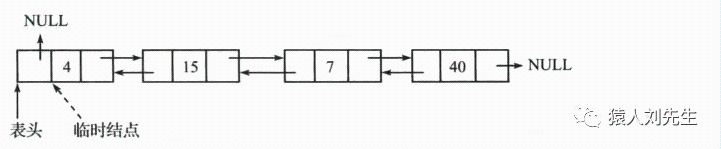
双向链表也叫双链表,是链表的一种,它的每个数据结点中都有两个指针,分别指向直接后继和直接前驱。所以,从双向链表中的任意一个结点开始,都可以很方便地访问它的前驱结点和后继结点。
1.5.4 单链表增加和删除
单链表头插
若需要在当前表头结点插入一个新结点 , 只需要修改一个next指针(新结点的next指针) , 可以分两步完成
* 修改新结点的next指针 , 使其指向当前的表头结点
* 更改表头指针的值 , 使其指向新节点(之前的表头指针指向的是15 , 修改后指向为新数据的)
单链表尾插
若需要在尾结点插入新结点 , 则需要修改两个指针(最后一个结点的next指针和新节点的next指针) , 可以分两步完成
* 新结点的next指针指向NULL
* 最后一个结点的指针指向新结点
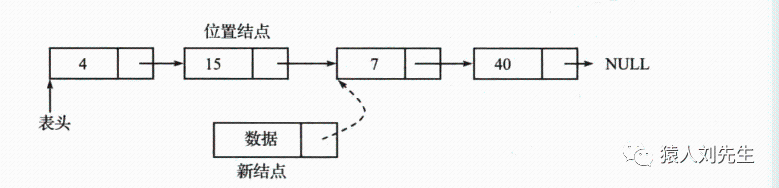
单链表中间插入
假设给定插入新结点的位置 , 在这种情况下需要修改两个指针 , 如果要在位置3增加一个元素 , 则需要将指针定位于链表的位置2 , 即需要从表头开始经过两个结点 , 然后插入新结点 , 为了简单起见 , 假设第二个结点为位置结点
*新节点的next指针指向位置结点的下一个节点
* 位置结点的next指针指向新节点
如果使用的是头插法 , 则时间复杂度为O(1) , 否则的话时间复杂度为O(N) , 而不管哪种方式插入空间复杂度为O(1)
单链表的头删
从链表中删除第一个节点 , 可以通过两步来实现
*创建一个临时节点 , 它指向表头指针所指的节点
* 修改表头指针的值 , 使其指向下一个结点 ,并移除临时结点(删除前 , 表头指针指向15 , 删除后 , 表头指针指向7)
单链表的尾删
单链表最后一个结点被删除 , 该操作比删除链表的头结点稍微复杂一点 , 因为需要找到表尾节点的前驱节点 , 所以分三步实现
* 遍历链表 , 在遍历时还需要保存前驱(前一次经过的)节点的地址 , 当遍历到链表的表尾时 , 将有两个指针 , 即表尾结点的指针和指向表尾结点的前驱节点的指针
* 将表尾结点的前驱结点的next指针更新为NULL
移除表尾结点的
单链表的中间删除
在这种情况下 , 被删除节点总是处于两个结点之间 , 因此不需要更新表头和表尾的指针 , 该操作可通过两步实现
* 在遍历时保存前驱(前一次经过的)节点的地址 , 一旦找到要被删除的结点 , 将前驱结点next指针的值更新为被删除结点的next指针的值
* 移除需删除结点的当前结点
如果使用的是头删法 , 则时间复杂度为O(1) , 否则的话时间复杂度为O(N) , 而不管哪种方式插入空间复杂度为O(1)
1.5.5 双向链表增加和删除
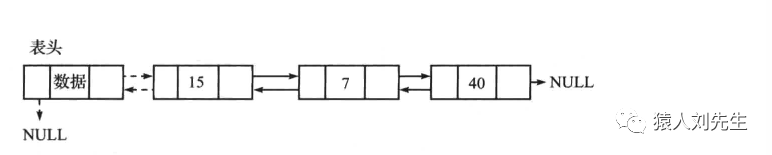
双向链表头插
这种情况下 , 需要修改前驱指针和后驱指针的值
*将新结点的后继指针更新为指向当前的表头结点 , 将新结点的前驱指针赋值为NULL
* 将表头结点前驱指针更新为指向新节点 , 然后将新结点作为表头
双向链表尾插
在这种情况下需要遍历到链表的最后 , 然后插入新结点
* 新结点的后继指针指向NULL , 其前驱指针指向表尾结点
* 更新最后一个结点的右指针 , 使其指向新结点
双向链表中间插入
需要遍历链表 , 知道位置结点 , 然后插入新元素
* 新结点的后继指针指向需要插入新结点的位置结点的后继结点。然后令新结点的前驱指针指向位置结点
*位置结点的后继结点的前驱指针指向新结点,位置结点的后继结点指向新结点
如果使用的是头插法 , 则时间复杂度为O(1) , 否则的话时间复杂度为O(N) , 而不管哪种方式插入空间复杂度为O(1)
双向链表头删
在这种情况下,要从双向链表中删除第一个结点(当前的表头结点)。可通过两步来实现
* 创建一个临时结点 , 它与表头指向同一个结点
* 修改表头结点指针 head(表头),使其指向下一个结点,将表头结点的前驱指针更改为NULL,然后移除临时结点。
双向链表尾删
这种情况的处理比删除双向链表的第一个结点要复杂一些,因为要找到表尾结点的前驱结点。需要3步来实现
* 遍历链表,在遍历时还要保存前驱(前一次经过的)结点的地址。当遍历到表尾时,有两个指针分别是指向表尾结点的tail(表尾)指针和指向表尾结点的前驱结点的指针
* 更新表尾的前驱节点的next指针为NULL
* 移出表尾结点
双向链表中间删除
在这种情况下,被删除的结点总是位于两个结点之间,因此表头和表尾的值不需要更新。该删除操作可通过两步实现
* 与上一种删除情况类似,在遍历链表时保存前驱(前一次经过的)结点。一旦找到要删除的结点,更改前驱结点的next指针使其指向被删除结点的下一个结点,更改被删除结点的后继结点的previous指针指向被删除结点的前驱结点。
* 移除被删除的当前节点
如果使用的是头删法 , 则时间复杂度为O(1) , 否则的话时间复杂度为O(N) , 而不管哪种方式插入空间复杂度为O(1)
1.5.6 循环链表增加和删除
循环链表头插
在循环链表的表头前插入结点与在表尾插入结点的唯一区别是,在插入新结点后,还需要更新指针。具体的步骤如下
* 创建一个结点 , 并且初始化其next指针指向该节点自身

* 更新表头的前驱结点的next 指针指向新结点,得到如下图所示的循环链表
* 设置新结点为表头结点
循环链表尾插
在由表头开始的循环链表的表尾插入一个包含数据(data)的结点。新结点将放在表尾结点(即循环链表的最后一个结点)的后面,也就是说,在表尾结点和第一个结点之间插入该新结点。
* 创建一个结点 , 并且初始化其next指针指向该节点自身
* 更新新结点的next指针为表头结点,然后遍历循环链表直至表尾。即插入位置应为循环链表中下一个结点是表头结点的结点位置(该结点是表头的前驱结点)
* 更新表头的前驱结点的next 指针指向新结点,得到如下图所示的循环链表
时间复杂度为O(N) , 用于扫描长度为N的链表 , 空间复杂度为O(1)
循环链表头删
删除循环链表中的第一个结点的操作很简单,只需将表尾结点的next 指针指向第一个结点的后继(下一个)结点。
* 遍历循环链表找到表尾结点。表尾结点是将要删除的表头结点的前驱结点。
* 创建一个指向表头结点的临时结点。更新表尾结点的next指针,使其指向第一个结点的后继结点
* 修改表头指针的值,使其指向后继结点。移除临时结点
循环链表尾插
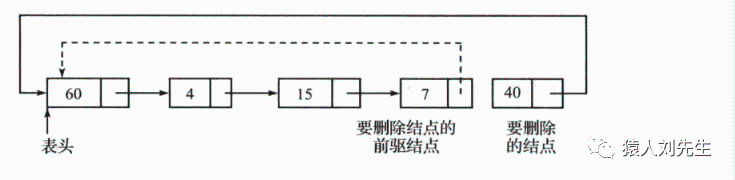
为了删除循环链表中的最后一个结点,需要遍历循环链表到倒数第二个结点。该结点将成为新的表尾结点,其next指针将指向链表的第一个结点。以下图的链表为例。为了删除最后一个结点40,首先遍历链表到结点7,再将结点7的next 指针指向结点60,并将这个结点重命名为表尾。
* 遍历循环链表,找到表尾结点及其前驱结点。
* 更新表尾结点的前驱结点的next指针,使其指向表头结点。
* 移除表尾结点
时间复杂度为O(N) , 用于扫描长度为N的链表 , 空间复杂度为O(1)
小结 :
-
单链表/双向链表头插/头删时间复杂度 : O(1)
-
单链表/双向链表中间插入/删除时间复杂度 : O(N)
-
循环链表插入/删除时间复杂度 : O(N)
-
单链表/双向链表/循环链表获取数据时间复杂度 : O(N)
-
数组头插/头删时间复杂度 : O(N)
-
数组尾删/尾插时间复杂度 : O(1)
-
数组中间插入/删除时间复杂度 : O(N)
-
数组/动态数组根据下标随机访问时间复杂度 : O(1)
-
数组/动态数组二分查找时间复杂度 : O(logn)
-
数组/动态数组顺序查找时间复杂度 : O(N)
-
动态数组头插/头删时间复杂度 : O(N)
-
动态数组尾插/尾删时间复杂度 : 不扩容 : O(1) , 扩容 😮(N)
-
动态数组中间插入/删除时间复杂度 : O(N)
今天的文章数据结构中链式存储结构有什么优势_数据结构中链式存储结构有什么优势分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/81417.html