线性表出
m个n维向量α1、α2……αm和m个数k1、k2……km,
称向量 k1 α1+k2 α2+……+km αm为向量α1、α2……αm的一个线性组合
若向量β可以表示成 :β= k1 α1+k2 α2+……+km αm,
则称β可以由向量组α1、α2……αm线性表出。
线性相关
对m个n维向量α1、α2……αm,
若存在 k1 α1+k2 α2+……+km αm=O 且k1、k2……km不全为零,
则称向量组α1、α2……αm线性相关。否则称线性无关。
线性无关的几种等价表述:(1)不存在不全为零的数k1、k2……km,使得k1 α1+k2 α2+……+km αm=O。(2)对任意不全为零的数k1、k2……km,均有k1 α1+k2 α2+…+km αm ≠ O。(3)当且仅当k1=k2=……=km=0时,才有k1 α1+k2 α2+……+km αm=O。
含有零向量/相等向量/成比例向量 的向量组是线性相关的。
单个向量时,零向量是线性相关的(存在k不为零,使得kO=O)。
定理:向量组α1、α2……αm(m>2)线性相关↔至少有一个向量ai可以由其余向量线性表出。 (k1 α1+k2 α2+……+km αm=O且k不全为零,等式两边移项即可得证)
定理:若向量组α1、α2……αm线性无关,而向量组α1、α2……αm、β线性相关,则β可以由α1、α2……αm线性表出,且表出法唯一。
定理:
1、向量β可由向量组α1、α2……αm线性表出↔
2、存在实数k1、k2……km,使得k1 α1+k2 α2+……+km αm=β↔
3、非齐次方程组Ax=β有解↔
4、系数矩阵的秩r(A)=增广矩阵的秩
(增广矩阵做初等行变换,化为行阶梯矩阵可得r(A)。再进一步化为行最简矩阵,可以列式求出多个未知数xi)
定理:
1、向量组α1、α2……αm线性相关(aj是n维列向量)↔
2、以αj为列向量的齐次方程组 x1 α1+x2 α2+……+xm αm=O有非零解↔
3、r(A)<n
原理:观察齐次方程组的系数矩阵Am×n=(α1,α2,…,αm),行数m=列向量aj的维度,列数n=向量的个数/未知数x的个数【这里的m和n的含义有所改变,要特别注意!记忆清楚!】【有几个列向量aj就有几个未知数】。
如何求r(A)——系数矩阵A由初等行(列)变换化为阶梯矩阵,阶梯矩阵的秩和原矩阵等秩。
推论1:m<n时,齐次方程组有非零解(系数矩阵的行数小于列数时,满足r(A)≤ m<n)
推论2:m=n时,当|A|=0时,齐次方程组有非零解(★只有n阶矩阵才有对应行列式。|A|=0说明在矩阵A内存在某行或列全部为0,满足r(A)<n)
★★★判断向量组的线性相关性,最多三种情况:列向量aj的维度=m,向量组中向量的个数=n
(1)m<n时:不用求直接得出r(A)<n,向量组线性相关。
原理:矩阵的秩≤行数,即r(A)≤ m<n,向量组线性相关 P232例5(2)
(2)m = n时(即系数矩阵为方阵时):计算系数行列式|A|
情况① |A|=0,则r(A)<n,向量组线性相关
情况② |A|≠0,则r(A) =n,向量组线性无关 只有方阵才有对应的行列式噢!P232例5(1)
(3)m>n时:计算系数矩阵A的秩r(A)
情况① r(A)<n,向量组线性相关
情况② r(A) =n,向量组线性无关
情况③ r(A)>n,向量组线性无关
题型:已知各向量的坐标,判断向量组的线性相关 就是转化为考察齐次方程组考察有无非零解。
步骤
1、设x1 α1+x2 α2+……+xm αm=O
2、按分量写出,得齐次方程组
3、写出系数矩阵Am×n=(α1,α2,…,αm)。观察。化为行阶梯矩阵判断r(A),若r(A)<n / m<n / m=n且|A|=0,齐次方程组有非零解,向量组线性相关。
定理:
向量组线性无关的充要条件:r(A)<n (n为向量的个数/齐次方程组未知数x的个数)
题型:已知α1、α2、α3线性无关,证明 α1+α2、α2+α3、α3+α1 线性无关。
步骤
1、记 β1=α1+α2、β2=α2+α3、β3=α3+α1
则(β1,β2,β3) =(α1+α2,α2+α3,α3+α1) =(α1,α2,α3)
(相当于矩阵(α1,α2,α3)右乘矩阵
)
2、由于行列式
=2≠0,知矩阵
可逆→r(β1,β2,β3)=r(α1,α2,α3)(乘上一个可逆矩阵不改变原矩阵的秩)
3、已知α1,α2,α3线性无关→r(α1,α2,α3)=n=3→r(β1,β2,β3)=3(向量组线性无关的充要条件为r(A)=n,n为向量的个数/齐次方程组未知数x的个数)
4、由于r(β1,β2,β3)=n,故β1,β2,β3也线性无关。(P234例10还有方法二)
向量组之间的线性表出:
一组向量由另一组个数更少的向量线性表出,则该组向量线性相关。
定理:设向量组β1、β2……βt中的任一向量均可由向量组α1、α2……αs线性表出,
(1)若β1、β2……βt 线性无关,t ≤ s(β数量少)
(2)若 t >s(β数量多),则β1、β2……βt 线性相关,
证明(2):设向量均为n维向量,因向量组β1、β2……βt中的任一向量均可由向量组α1、α2……αs线性表出,存在。。。(未完)
(1)是(2)的逆否命题。
今天的文章线性表示向量_线性相关和线性表示分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/81649.html


 (相当于矩阵(α1,α2,α3)右乘矩阵
(相当于矩阵(α1,α2,α3)右乘矩阵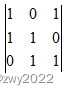 =2≠0,知矩阵
=2≠0,知矩阵