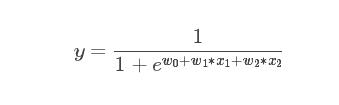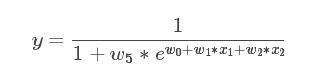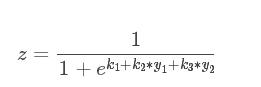线性和非线性函数_如何区分线性和非线性微分方程

一、线性函数与非线性函数的区别

线性Line，是指量与量之间按照比例成直线关系，在数学上可理解为一阶导数是个常数；
非线性non-line则指不按照比例不成直线关系，一阶导数不为常数。

参考链接：
机器学习中的线性和非线性判断
这篇博客的结论是：
下面可以快速判断是为非线性的三种常见情况：

(变量)^n，且n不为1
|变量| 有变量在绝对值內的为非线性
sgn(变量) 有变量在符号函数之内

做一点补充理解：
线性定义：F(ax+y) = aF(x) + F(y)，x，y为变量，a为常数；
问题：一个显而易见的事实，一次函数 F(t)=3t + 2 (t为标量实数)是一个线性函数，那么根据线性定义，应有F(2t) = 2F(t)，然而
F(2t) = 32t + 2 = 6t + 2；
2F(t) = 2(3t+2) = 6t + 4；
看起来两者并不相等，为什么？
得出两者并不相等的原因是将变量 t 当做标量，也就是认为线性定义中的变量 x，y 是标量，但实际上线性定义中的变量x，y是指向量，F是向量变换，满足线性定义的向量变换可称为向量的线性变换。

一次函数F(t)=3t + 2 (t为标量实数)也是线性函数，那么根据前面的线性定义，应当如何解释 F(2t) 与 2F(t)的关系？
从向量视角下去理解一次函数 F(t)=3t + 2 (t为标量实数)，t 是只有一个标量作为分量的向量，2F(t)和F(2t)亦如此，向量F(2t)平移即可得到2F(t)。
两个向量是同一个向量的条件：方向相同；长度相等。向量
F(2t)=6t + 2;
2F(t)=6t + 4；
两者都可以通过向量 6t 平移得到，由于平移不改变向量的方向和长度，故向量F(2t)=2F(t)=6t。

怎样区分线性和非线性：

非线性函数：不满足线性定义的函数即为非线性函数。
线性可以认为是1次曲线，比如比如y=ax+b ，即成一条直线；
非线性可认为是2次以上的曲线，比如y=ax²+bx+c，（x²是x的2次方），即不为直线的即可。
两个变量之间的关系是一次函数的关系图像是直线，这样的两个变量之间就是“线性关系”如果不是一次函数关系，图像不是直线，就是“非线性关系”。
线性与非线性，常用于区别函数y = f （x）对自变量x的依赖关系。线性函数即一次函数，其图像为一条直线。其它函数则为非线性函数，其图像不是直线。
在数学上，线性关系是指自变量x与因变量yo之间可以表示成y=ax+b ，（a，b为常数），即说x与y之间成线性关系。

总结：
不能表示成y=ax+b ，（a，b为常数），即非线性关系，非线性关系可以是二次，三次等函数关系，也可能是没有关系。

二、线性模型和非线性模型的区别

1、线性模型可以是用曲线拟合样本，但是分类的决策边界一定是直线的，例如logistics模型
　　2、区分是否为线性模型，主要是看一个乘法式子中自变量x前的系数w，如果w只影响一个x，那么此模型为线性模型。或者判断决策边界是否是线性的
　　3、举例：

画出y和x是曲线关系，但是它是线性模型，因为x1*w1中可以观察到x1只被一个w1影响

此模型是非线性模型，观察到x1不仅仅被参数w1影响，还被w5影响，如果自变量x被两个以上的参数影响，那么此模型是非线性的！

4、其实最简单判别一个模型是否为线性的，只需要判别决策边界是否是直线，也就是是否能用一条直线来划分
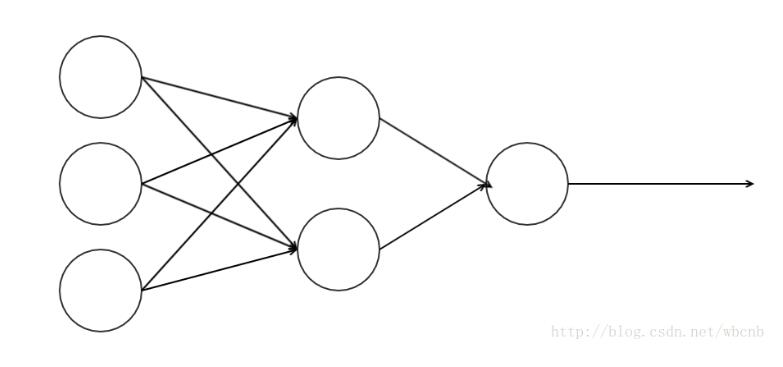
　　神经网络是非线性
　　虽然神经网络的每个节点是一个logistics模型，但是组合起来就是一个非线性模型。
　　此处我们仅仅考虑三层神经网络

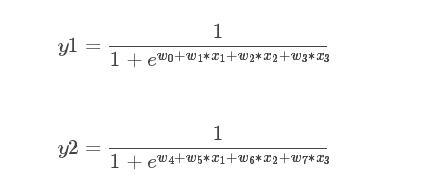
　第一层的表达式

　第二层的表达式

将第一层的表达式带入第二层表达式中，可以观察到x1变量不仅仅被w1影响还被k2影响，所以此模型不是一个线性模型，是个非线性模型。