单样本的z检验_单样本z检验的前提条件

提出问题：想知道北京大学所有男生的平均身高是否等于1.8米。

1、抽样（比如抽取100人作为样本）。

2、做出假设，假设北京大学男生总体的平均身高等于1.8米。（零假设，null hypothesis）。

这里用假设检验来判断样本所代表的总体的均数是否等于1.8米，本质是判断零假设成立的前提下（假设总体均数等于1.8米），是否有可能抽到目前这个样本及更极端的样本。

关于假设检验的基本思想，读一下这篇你就懂了：我来尝试给你讲清统计学中的假设检验和两类错误

3、基于当前零假设和当前样本，计算 z score （z值）或t score（t值），通过z值 / t值及比该数值更极端的值出现的概率来代表抽到目前这个样本及更极端的样本的概率。其计算公式如下。

总体标准差已知则计算z值即可，但大多数情况下总体标准差是未知的，此时用样本标准差代替，计算t值。

在本例中，先计算样本均数和样本标准差，即sample mean和sample standard deviation，也就是说z值和t值都是在当前抽到的样本的基础上计算得到的，如果重新抽样，z值和t值可能会变化；

true mean under null hypothesis就是我们零假设中设定的1.8米，也就是说z值和t值都是在零假设成立的前提下计算得到的数值；

true standard deviation是北京大学所有男生这个总体身高的标准差，需根据实际情况判断是否能够获得这一数据进而决定用z值还是t值。

4、在计算完z值或t值之后，如何判断z值 / t值及比该数值更极端的值出现的概率有多大？什么叫做『更极端的值』？概率小到多少就认为是不可能发生呢？

z值服从标准正态分布，t值服从t分布（近似正态分布的一簇曲线，均数为零），某一段分布曲线下的面积就是某一取值范围的z值 / t值出现的概率。

注意：这里的表达必须是『某一取值范围的z / t值出现的概率』，因为z分布和t分布分别是z值和t值的概率分布，单个数值对应的概率是0。

在z分布或t分布中，随着曲线向两端延伸，其对应的z值 / t值的绝对值越来越大，此时我们认为z / t的取值越来越极端，z值 / t值及更极端的值出现的概率越来越小。

通常假设检验中认为概率小于5%的事件在一次抽样中是不可能发生的。

如下图。

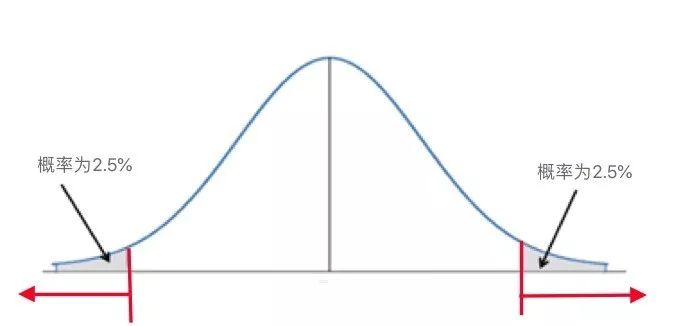
z分布或t分布曲线
双侧检验
红色箭头所指的横轴区域表示z值/t值及更极端的值
灰色阴影部分表示z值/t值及更极端的值发生的概率，为5%
也就是说，在零假设成立前提下，基于目前抽到的样本，我们的检验思路如下：

计算得出的z值/t值落在红色箭头范围内 → 在一次抽样中，抽中目前样本及更极端的样本的概率小于5% → 在一次抽样中，目前样本及更极端的样本不可能被抽中 → 拒绝零假设。

由计算公式可知，z值和t值就是目前抽到的这个样本的均数与零假设中规定的总体均数之间的差异。

我们通常说：想判断这个差异有没有统计学意义，其实是想判断在零假设成立的前提下（假设总体均数等于1.8米），是否有可能得到目前这个样本并计算出目前这个差异。

『有可能得到』就是我们常说的差异没有统计学意义，还没有理由拒绝零假设；『不可能得到』就是差异有统计学意义，拒绝零假设。

本例是双侧检验，单侧检验的结论推断方法和双侧检验一样，大家可自行练习。

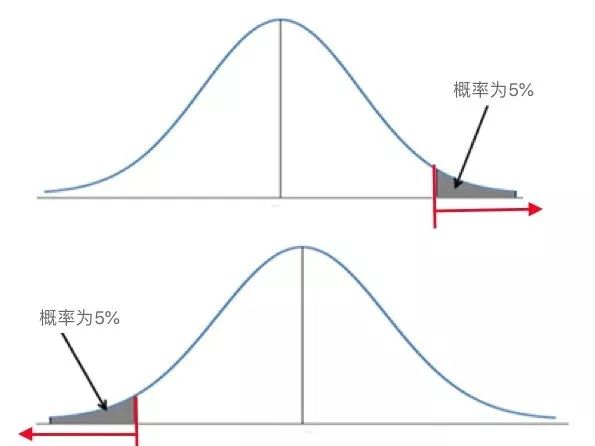
z分布或t分布曲线
单侧检验的两种情况
红色箭头所指的横轴区域表示z值/t值及更极端的值
灰色阴影部分表示z值/t值及更极端的值发生的概率，为5%

5、最后，根据目前得到的z值或t值是否落在红色箭头的范围内，得到假设检验的结论。

如果你计算得到的z或t值落在了非红色箭头的范围内，就意味着零假设成立的前提下，目前样本是有可能被抽中的（目前的样本已经被抽中了，这是事实），也就是说零假设是符合事实的，所以我们没有理由拒绝零假设。

相反，如果z或t值落在了红色箭头的范围内，就意味着零假设成立的前提下，目前的样本在一次抽样中是不可能发生的（这是违反事实的），那么你就有理由怀疑零假设的真实性，从而拒绝零假设。

注意：z检验和t检验的关键在于，z值和t值分别服从标准正态分布和近似正态分布的t分布。所以为了保证你计算出来的z值/t值服从上述分布，就要保证样本所来自的总体服从正态分布或近似正态分布。这是单样本z检验/t检验的前提条件。

今天的文章单样本的z检验_单样本z检验的前提条件分享到此就结束了，感谢您的阅读。