capcom优化好_cpu优化器

在较早的文章中介绍了些Volcano/Cascades优化器框架的设计理念和实现思路，基本是基于论文的解读:

https://zhuanlan.zhihu.com/p/364619893

https://zhuanlan.zhihu.com/p/365085770

虽然cascades号称目前最为先进的优化器搜索框架，但不得不说这2篇paper的内容，实在是让人看起来有些吃力。尤其是后篇，说是从工程实现的角度来描述，但讲解的不够详尽，而且有些地方既模糊又抽象。

此外工业界并没有一款优化器是完全基于paper的框架去实现的，这让我们按图索骥变得更加困难，不过今天介绍的这篇paper 《EFFICIENCY IN THE COLUMBIA DATABASE QUERY OPTIMIZER》，为理解cascades提供了很好的参考，并且提供了开源实现。

概括来说，这篇paper详细讲解了columbia optimizer的设计和实现，它完全参考了cascades中的概念和top-down的搜索策略，并做了一系列优化来改善cascades的优化效率。

本文将分为以下几个方面进行介绍：

Cascades优化器的基本概念
Columbia优化器的设计和实现
Calcite中对于Cascades实现的参考

Cascades优化器的基本概念

查询优化的本质，是

给定query和代价模型等元信息的前提下，搜索计划空间的所有可能，得到代价最低的执行计划。

这是一个NP hard问题，人们通常会利用dynamic programming的思想，将其转换为一个problem和其包含的一系列嵌套的subproblems。通过递归获取子问题的最优解并向父问题延伸，最终得到根问题的最优解。

cascades的优化框架也遵循了这个思路，只不过与system-R等不同，它不采用子problem -> 父problem的直观路线，而是从父problem -> 子problem深度优先递归方式，也就是所谓的top-down search strategy，并在过程中利用memorization避免对相同子problem的反复计算。深度优先的好处是可以尽早获取到一个可行的物理计划和对应cost，并以该cost作为上界在后续search中做剪枝。

关于cascades这里只大概给出一些基本概念，方便理解文章后续的内容，总的来说还是需要读者有cascades的基本理论知识，详细的内容可以参见前面的文章或读原paper。

operator

描述某个特定的algebra运算，对于关系代数就是例如join / aggregation等。分为logical/physical两类

logical operator描述算子的逻辑语义，与具体实现无关。
physical operator描述算子的具体实现算法，例如对join有hash join/nested loop join等。

expression

在计划空间中描述一个具体的algebra运算内容的数据结构，如果是关系代数那就表示一个关系运算表达式。内部会包含对应该运算的operator，根据operator的不同类型分为logical expression/physical expression。一般一个logical expression会对应多个具体实现的physical expressions。

logical property

运算结果所具有的逻辑属性，这类属性与运算的语义相关，与具体实现无关，例如数据的cardinality/schema等。

physical property

运算结果所具有的物理属性，这类属性与具体实现方式相关，例如数据的collation(顺序)/distribution等。

group

上面提到了优化的过程是对problem/subproblems的求解，由于问题的复杂性，dynamic programming会对problem做一定的“拆分”，而group就是按照逻辑等价性进行拆分的结果，不同group对应不同的subproblem，从而把问题规模不断减小。

具体到实现中，group是所有逻辑上等价的expression的集合，其中所有expression(包含logical expression + physical expression)的逻辑属性相同，构成逻辑等价类。

search space

存放优化过程中所有枚举的计划的数据结构，随着优化过程的进行会生成若干潜在的候选plan tree，内部会利用memorization来避免生成重复的计划内容，减少无谓空间/时间浪费。

search space是基于group来组织的，所有各类expression包含在所属group内部。所以组织层次上是

search space -> group -> m-expr

rule

rule是搜索算法中最为核心的部分，各种计划(节点)的生成是通过rule来完成的，rule总是应用到一个logical expression上，将其转换为另一种logical expression或者一个physical expression。

logical -> logical的转换，称为transformation rule。

logical -> physical的转换，称为implementation rule。

无论是哪种rule，都包含两个最主要的结构：

Pattern: 描述rule可以应用到的表达式形态。
Substitute ：描述转换之后的表达式形态。

因此一个rule是否可以应用，要判断Pattern是否和现有的expression tree能match上，可以的话，就把substitute对应的新expression tree建立起来，加入search space中，作为候选计划的一部分，从而实现对计划空间的扩展。例如，一个transformation rule是predicate pushdown，那它所要求的pattern就必须是

如果expression tree上是join -> join，则不满足这个pattern而无法应用这个rule。转换后的substitute为：

enforcer

由于cascades的搜索过程是top-down的，这意味着对当前的expression tree优化时，总是先处理root expression，一旦确定了其物理执行算法，会向children做递归优化，这时root expression的物理实现可能会对children的输出物理属性有所要求，例如top join如果使用sort merge join，则要求2个input在对应的join key上是有序的，这种对物理属性的要求构成了optimization goal的一部分。

enforcer是一个physical operator，作用是改变input group的物理属性，来满足上层算子的要求。

Columbia的设计与实现

这节参考了paper的主要内容，着重介绍search engine的设计实现和相对cascades对于搜索效率的改进。

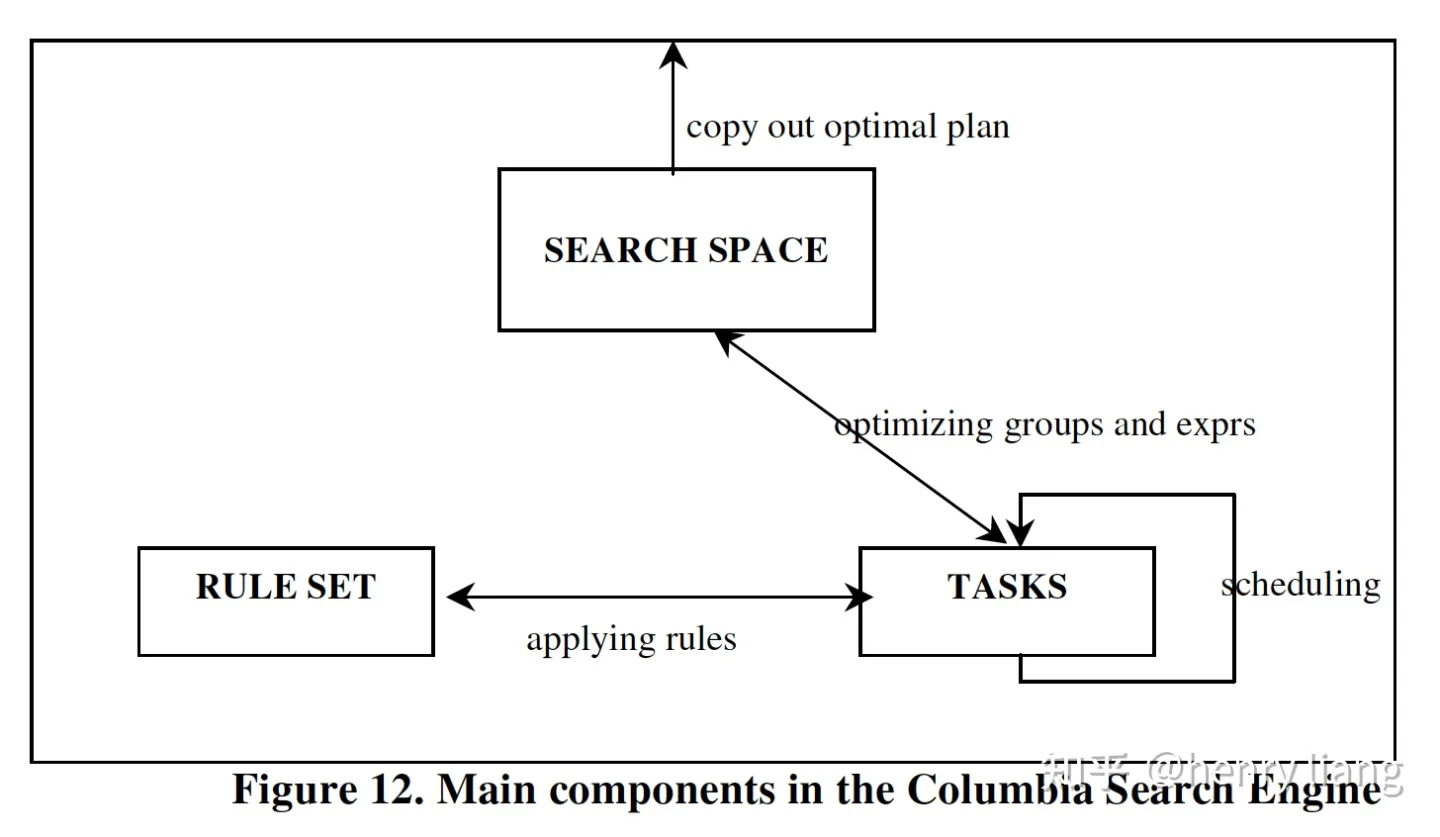
三大组件：

这里的基本思路和cascades一样，通过不同类型的task来驱动整个优化流程，扩展seach space，task的核心是对rule的应用。

Search Space

首先介绍一个columbia optimizer中的重要概念，multi-expression：

一个query在经过parser后会被转换为由expression（缩写expr) 组成的AST，而multi-expression（缩写m-expr）则是expr的”紧凑”版本，两者共享了描述运算语义的operator对象，但expr的输入是子expr，而m-expr的输入则是子group，其内部是任意满足该运算语义的m-expr集合，例如对于表达式：

(t1 inner_join t2) inner_join (t3)

其left input是 (t1 inner_join t2)，但这仅是一个逻辑运算符，内部可能对应

t1 inner_join t2 / t2 inner_join t1 / t1 hash inner join t2 / t2 nested loop inner join t1 …..

等很多的具体表达式（logical/physical），但都属于同一个group。

m-expr是group中的主要组成成员，优化过程也主要基于m-expr进行。

在构建初始search space时，会把parser生成expr tree CopyIn search space中，形成一系列basic groups，这些group中只有一个initial logical m-expr，与AST中的expr一一对应。后续优化中，group中的m-expr会不断增加，或者search space中产生新的group。

SSP (Search Space,对应Memo)
|-> groups (array)
       |-> m-exprs
              |-> operator (logical/physical)
              |-> input groups (array)

代码中几个主要结构类和内部一些重要成员：

class SSP	//Search Space
{
public:
	M_EXPR ** HashTbl;	// To identify duplicate MExprs
	// Convert the EXPR into a Mexpr. 
	// If Mexpr is not already in the search space, then copy Mexpr into the 
	// search space and return the new Mexpr.  
	// If Mexpr is already in the search space, then either throw it away or
	// merge groups.
	// GrpID is the ID of the group where Mexpr will be put.  If GrpID is 
	// NEW_GRPID(-1), make a new group with that ID and return its value in GrpID.
	M_EXPR * CopyIn(EXPR * Expr, GRP_ID & GrpID);	
	
	//If another expression in the search space is identical to MExpr, return 
	// it, else return NULL. 
	// Identical means operators and arguments, and input groups are the same.
	M_EXPR * FindDup (M_EXPR & MExpr);		
private:
	GRP_ID	RootGID;	//ID of the oldest, root group.  Set to NEW_GRPID in SSP""Init then
        //Collection of Groups, indexed by GRP_ID
        CArray<GROUP*, GROUP* > Groups;
}; // class SSP

class GROUP      
{	
public:
	GROUP(M_EXPR * MExpr); //Create a new Group containing just this MExpression
	inline GRP_ID GetGroupID() {return(GroupID); };
	
	//Return winner for this property, null if there is none
	WINNER * GetWinner(PHYS_PROP * PhysProp); 
	//Create a new winner for the property ReqdProp, with these parameters.
	//Used when beginning the first search for ReqdProp.
	void NewWinner(PHYS_PROP *ReqdProp, M_EXPR * MExpr, COST * TotalCost, bool done);
private	: 
	GRP_ID	GroupID;	        //ID of this group
	M_EXPR * FirstLogMExpr;	        //first log M_EXPR in  the GROUP
	M_EXPR * FirstPhysMExpr;	//first phys M_EXPR in  the GROUP
	LOG_PROP *	 LogProp;       //Logical properties of this GROUP
	COST * LowerBd;			// lower bound of cost of fetching cucard tuples from disc
	// Winner's circle
	CArray < WINNER *, WINNER * > Winners;
};  // class GROUP

class M_EXPR 
{
private:
	M_EXPR * HashPtr;			// list within hash bucket
	BIT_VECTOR 		RuleMask;	//If 1, do not fire rule with that index
	OP*		Op;					//Operator
	GRP_ID*	Inputs;
	GRP_ID 	GrpID;				//I reside in this group

	inline int GetArity() {return (Op -> GetArity()); } ;
	//We just fired this rule, so update dont_fire bit vector
	inline void  fire_rule(int rule_no) { bit_on( RuleMask , rule_no); };	
}; // class M_EXPR

class WINNER    
{
private:
	M_EXPR    *   MPlan;
	PHYS_PROP *  PhysProp;       //PhysProp and Cost typically represent the context of
	COST      *  Cost;           //the most recent search which generated this winner. 
	bool		 Done;	     //Is this a real winner; is the current search complete?
}; //class WINNER

search space的总体设计与cascades没什么不同，但做了如下改进

GROUP

为了提升搜索效率，针对group做了2点改进

引入lower bound cost，做更积极的group pruning

在top-down的优化中，具体到某个group时，会有对应的search context（cascades中的optimization goal)，context中包含2个部分：

[required physical property , cost upper bound]

也就是在向下搜索时，要求当前group输出的物理属性，同时整个子计划的代价要小于cost上界。

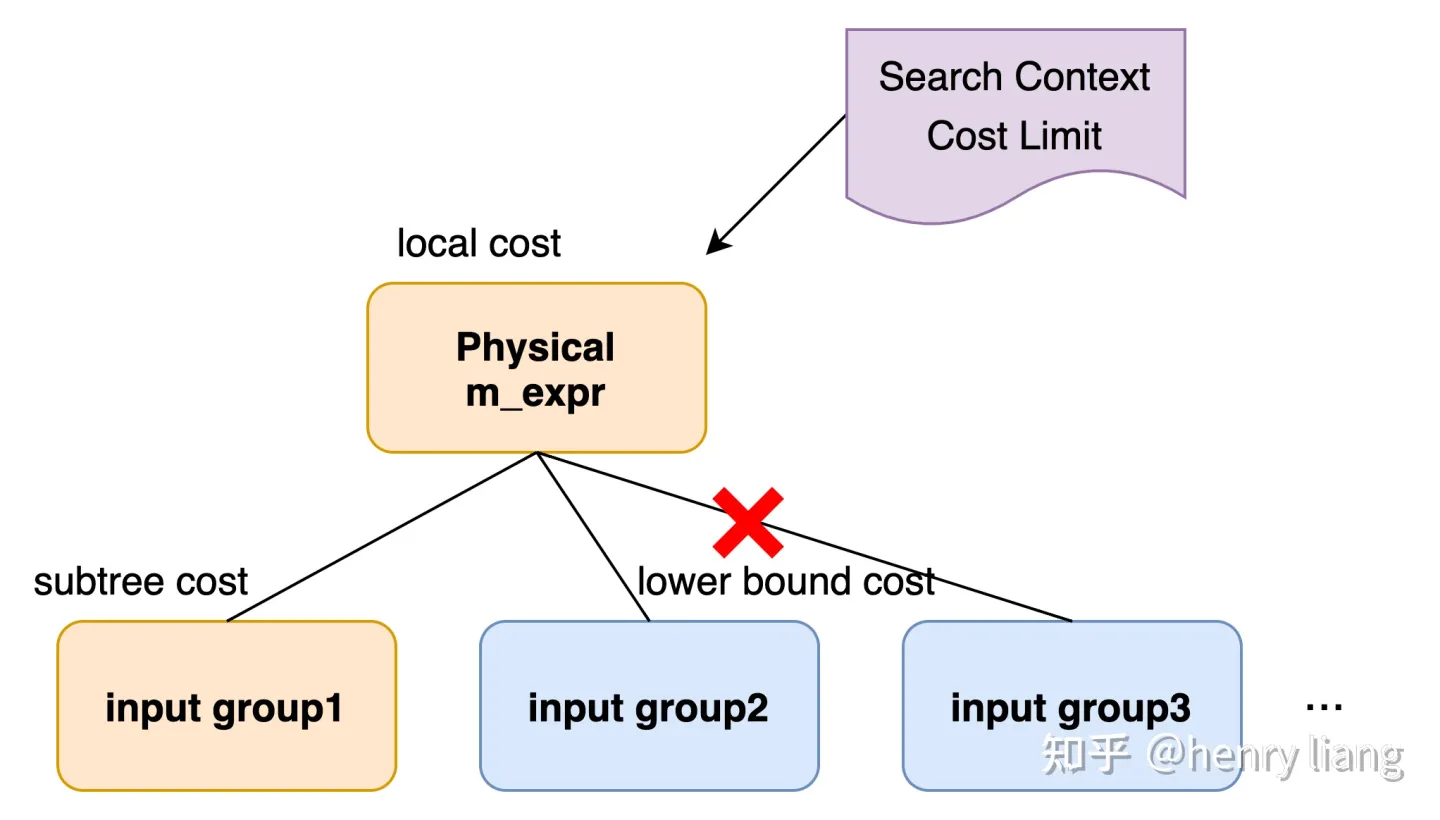
子计划的代价是当前group的physical m-expr代价 + 各个input group中最优physical m-expr的代价。有没有可能在优化input group之前，就能判断其代价已经过大了，从而实现pruning呢？

columbia为每个group计算一个cost lower bound，并保证group枚举的任一physical m-expr对应的子plan，其cost(m-expr) > lower bound。这个lower bound是基于group的logical property计算的，和具体算子实现方式无关，在group创建时计算完成。

剪枝过程如下图，top group的physical m-expr已生成并可得到该算子的local_cost，在依次优化下层input group时，假设input group1已优化完得到subplan cost1，而input group 2/3尚未优化，但此时

top local cost + input cost1 + input_group2’s lower bound cost > Cost Limit

表明无法找到满足context的最优解，从而避免了对input group 2/3的无意义优化。

lower bound cost的具体算法如下：

|G| = group输出的cardinality

cucard(Ai.X) = Ai.X这列在G的输出结果中具有的最大NDV值

cucard(Ai) = max(cucard(Ai.X)) 表示对于所有在G输出结果中的Ai表的列，具有的最大NDV值

touchcopy() = 对一行join结果做拼接并copy出去的代价

Fetch() = 通过IO读取一行数据的代价

这个公式给出了一个join plan的总代价：

LowerBound(join sequence) = cost(top join) + cost(non-top join) + cost(base table fetch)

对于cost(non-top join)的部分，我们考虑t1 join t2 … join tn 这个序列，且以left-deep tree为例：

non top join = t1 join t2 … join tn-1

如果t2在G中具有cucard(t2)个NDV值，说明t1 join t2至少产生了cucard(t2)行数据，对t3…tn-1也同理类推，由于计算的是下界，这是安全的。paper中证明了即使不是left-deep tree这个推导也成立，这里不再详述。

Lower bound pruning是columbia对优化效率的一个重要改进，可以很好的提升剪枝效率，缩短优化时间，同时由于是基于代价模型计算的cost下界，这种pruning并不影响结果的最优性。

2. 将logical m-expr和physical m-expr分离到2个链表中

在cascades中，所有m-expr是保持在一个link list中，而columbia则分为了logical/physical两个list，这在2种情况下有益：

优化一个group时，会对所有logical m-expr做rule binding的操作，如果是一个list则要跳过physical m-expr，考虑到group中的m-expr可能很多，而且physical m-expr数量会是logical m-expr的N倍，因此可能引发较多memory page fault。而rule binding是一个密集操作，因此微小的改进也有意义。
一个group可能会基于不同的search context（例如不同required physical property）反复被优化，因此将之前生成的physical m-expr保存在一起，当下次优化时可以先检查是否已经有physical m-expr能够满足新context的要求，如果可以则直接进入针对该m-expr的优化流程。而在cascades中，每个group并不特殊处理physical m-expr，总是要对所有logical m-expr重新优化来生成physical m-expr，这显然不够高效且浪费空间。

WINNER

由于group会基于不同search context反复优化，因此每个context应该都会找到一个最优plan，这些plan就保存在group的winners数组中，以备后续复用。

在columbia中，WINNER结构被简化，只包含

[当前group中最优的(physical) m-expr + 最优plan cost + required physical property]

在基于当前search context搜索过程中得到的最优解（临时）也会保存在winner结构中。此外，如果最后无法找到满足要求的plan，这个winner对象仍然会创建出来，只不过其中的m-expr是null pointer，表示无法找到context的最优解，这也是一种结果，可以保存下来被复用。

M_EXPR

前面已经提到了EXPR和M_EXPR，以及何时从EXPR生成M_EXPR。相对于cascades中用来描述该结构的EXPR_LIST，columbia的M_EXPR要更加精简。

注意在上面代码中M_EXPR类的这个字段

BIT_VECTOR 		RuleMask;  // 每个rule对应一个bit，如果fire过则设为1

RuleMask实现了columbia中的unique rule set原则，也就是对于一个m-expr，任一个rule只会对其fire(尝试apply)一次，不会做重复的计算，这对于提升搜索效率很重要，同时可以保证不会生成重复的physical m-expr。但注意logical m-expr的唯一性只通过unique rule set是无法保证的，因为可能有不同的logical m-expr通过不同的transformation rule生成同样的logical m-expr。因此需要在整个search space中建立logical m-expr的去重机制。这通过SSP的

M_EXPR ** HashTbl;	// To identify duplicate MExprs

这个成员完成，这是一个针对logical m-expr的hash table

其key是[operator name, operator parameters, input group numbers]，value就是对应的m-expr pointer。

hash table的实现仍然是静态的buckets + linked list，只是做了2点改进：

使用了更加简单高效的hash function lookup2.
buckets的数量不再是一个质数而是2的幂，mod操作更高效

考虑到logical m-expr的生成是个非常频繁的操作，结构的精简+查找效率提高是不错的空间/时间优化。

Rules

rule是对m-expr进行优化的主要工具，rule和search space的定义、search strategy的定义是正交的，因此可以独立的进行扩展。

在columbia中，rule的基类定义如下：

class RULE
{
private : 
	EXPR    *  original;     // original pattern to match
	EXPR	*  substitute;   // replacement for original pattern
				 //"substitute" is used ONLY to tell if the rule is logical or physical,
				 // and, by check(), for consistency checks.  Its pattern is represented 
				 // in the method next_substitute()
	CString    name;
	BIT_VECTOR mask;	 //Which rules to turn off in "after" expression
	int index;		 // index in the rule set
	
public :
	bool top_match (OP *op_arg)
	{
		assert(op_arg->is_logical()); // to make sure never O_EXPR a physcial mexpr 
		
		// if original is a leaf, it represents a group, so it always matches
		if( original->GetOp()->is_leaf()) return true;  
		
		// otherwise, the original pattern should have a logical root op
		return ( ((LOG_OP *)(original->GetOp()))->OpMatch((LOG_OP *)op_arg) ); 
	};
	
	virtual int promise ( OP * op_arg, int ContextID)
	{	return ( substitute->GetOp()->is_physical() ? PHYS_PROMISE : LOG_PROMISE); };
	
	virtual bool condition ( EXPR * before, M_EXPR *mexpr, int ContextID)
	{ return true; };
	
	//Given an expression which is a binding (before), this
	// returns the next substitute form (after) of the rule.
	virtual EXPR * next_substitute (EXPR * before, PHYS_PROP * ReqdProp)=0;
}; // RULE

其中最重要的结构就是original(pattern)和substitute，他们都是用EXPR来构建的tree(logical operator的tree)。

在其中有一种特殊的operator: leaf operator，他是expr tree的叶子节点，起到通配作用，可以match任意子表达式。例如inner join的结合律：

RULE EQJOIN_LTOR
Pattern:     ( L(1) join L(2) ) join L(3)
Substitute:  L(1) join ( L(2) join L(3) )

其中L就是leaf operator，在APPLY_RULE这个task中，会进行pattern match，建立rule和top m-expr的绑定关系(rule binding)，然后通过substitute来生成新的m-expr/group对象，加入search space中。具体包含2个主要函数：

创建BINDERY对象，递归做pattern matching，过程中可能产生很多rule binding
对每个binding，RULE::next_substitue创建对应的新m-expr tree，并通过SSP::copy_in加入search space中

此外，RULE对象还有些方法辅助这个apply过程：

top_match() 用来比较rule的top operator和当前root m-expr的top operator，相当于预检查，如果不匹配可以快速skip。
promise() 基于当前的search context对rule进行打分，分数越高表示rule对于优化越有意义，同时promise值可以决定rule是否会尝试apply，promise <= 0时，不做apply。默认implementation rule的promise = 2，而transformation rule的promise = 1，因此implementation具有更高的优先级，总是会优先生成physical m-expr并递归优化下去，这样有助于尽快找到尽量优的physical plan tree，保证深度优先的机制，也有利于后续优化做基于cost limit的剪枝。

Rule Binding

仍然以上面的EQJOIN_LTOR结合律为例

Pattern:     ( L(1) join L(2) ) join L(3)
Substitute:  L(1) join ( L(2) join L(3) )
Target m-expr: (G7 join G4) join G10

针对每个group，会创建一个BINDERY对象，负责将pattern与该group中所有logical m-expr做binding。

本例中

一个expression bindery对象会用来匹配top expr和top logical m-expr。
一个group bindery对象对left input group的所有logical m-expr做检查，建立多个的binding：

L(1) join L(2) <=> G7 join G4

L(1) join L(2) <=> G4 join G7

3. 另一个group bindery对象对right input group做检查，但只会建立一个binding

L(3) <=> G10

具体绑定算法用一个基于3个状态的有限状态机来实现，并通过BINDERY::advance()方法来驱动，不断寻找binding：

typedef enum BINDERY_STATE
{
        start,          // This is a new MExpression
	valid_binding,  // A binding was found.
	finished,       // Finished with this expression
} BINDERY_STATE;

advance的伪代码如下：

基本思路就是深度优先的方式，不断找input group中的binding，再返回上层group找，直到top m-expr，具体到m-expr的匹配则是比较operator的id和arity，可参考实现源码。

Enforcer Rule

前面已经提到enforcer是一种physical operator，因此enforcer rule也算是implementation rule，会生成对应的enforcer m-expr，属于physical m-expr，其input group就是原来的group，只是改变了physical property。例如SORT_RULE是一个enforcer rule，在substitute中会以QSORT这个operator作为top operator，即：

SORT_RULE
Pattern: L(1)
Substitute: QSORT L(1)
L(1) 是任意leaf operator

只且仅当group的search context中有physical property requirement时，enforcer rule才会被考虑(promise > 0)。

对于enforcer rule的处理在columbia和cascades中非常不同：

没有excluded property

在cascades中，search context中会包含额外一项：excluded properties，即禁止生成某种物理属性，这是为避免重复apply enforcer rule而产生多个冗余的enforcers，但不同的search context下仍然会生成多个对应physical property要求的enforcer。

在columbia中，enforcer rule被加入到RuleMask当中，这样通过unique rule set机制可以避免反复生成enforcer，但也带来了一个问题：group第一次被优化后生成了enforcer m-expr，后续如果基于不同search context再优化，就无法再生成新的enforcer导致计划空间枚举不全。columbia通过复用enforcer m-expr来解决该问题。

2. 复用enforcer m-expr

在cascades中，enforcer的operator包含参数，例如QSORT(A.x) 和 QSORT(A.y)是两个不同的enforcer m-expr，都会生成在group中，应对不同context的物理属性要求。

在columbia中，enforcer的operator不包含参数，只是行为描述，这样一个group只会有一个enforcer m-expr，同时在优化group时，一定要对所有已有的physical m-expr检查是否满足物理属性要求，这时如果遇到enforcer m-expr，则忽略参数认为可满足，从而进入physical m-expr的优化流程，这里会对enforcer m-expr和其输入重新计算cost，如果是最优plan则记入winner中。后续可以从WINNER类的physical property成员补全对enforcer的完整描述，弥补parameter的缺失。

这种处理方案有些tricky，但也减少了enforcer m-expr的数量，节约空间。

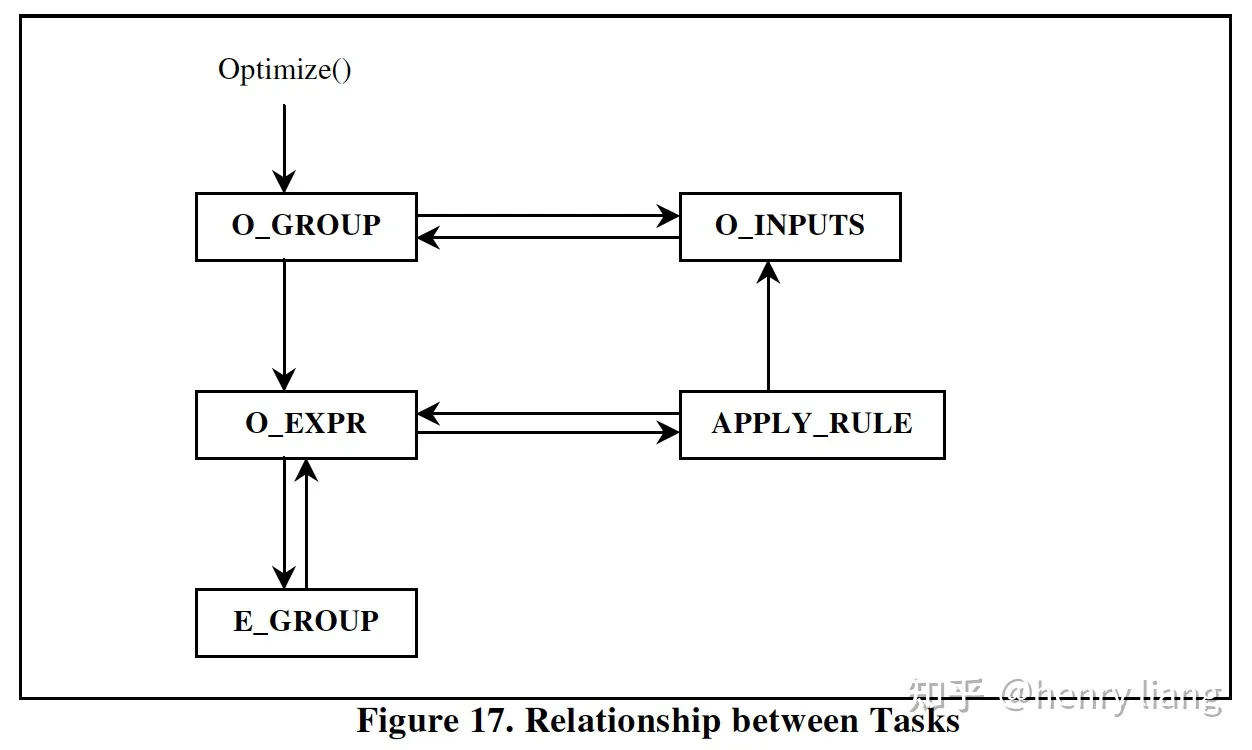
Tasks

task是搜索过程的任务单元，现有task的执行会创建和调度新的task。每个task都对应着当前优化的search context。对task的介绍也是对整个优化流程的介绍，这里仍会结合代码。

class TASK
{
	friend class PTASKS;
private :
	TASK        * next;         // Used by class PTASK
protected :
	int	 ContextID;      // Index to CONT::vc, the shared set of contexts
	int      ParentTaskNo;   // The task which created me   
public :
	virtual void perform ()=0;	//TaskNo is current task number, which will
}; // TASK

class PTASKS
{
private :
	TASK        * first;        // anchor of PTASKS stack
public :
	void push (TASK * task);
	//##ModelId=3B0C085D016B
	TASK * pop ();
}; // PTASKS

所有具体task都是TASK的子类，和cascades paper中一样，task以stack的方式来调度。有了这种抽象，优化的流程实际很简单：

void SSP::optimize()
{	
	//Create initial context, with no requested properties, infinite upper bound,
	// zero lower bound, not yet done.  Later this may be specified by user.
	PTasks.push (new O_GROUP (RootGID, 0, 0));
		
	// main loop of optimization
	// while there are tasks undone, do one
	while (! PTasks.empty ())
	{
		TaskNo ++;
                TASK * NextTask = PTasks.pop ();
		NextTask -> perform ();
        }
}  // SSP::optimize()

在columbia中，task共分为5种，其相互调用关系如下：

O_GROUP: 优化一个group

这是对plan/subplan做优化的最外层入口，会找到在特定search context下，这个group作为root的最优plan，保存到group的winner数组中。它会生成所有必要的logical/physical m-expr，并计算cost。伪代码如下：

如果lower bound已经大于upper bound，则没必要优化，无解
如果已经对这个context得到了winner，直接返回

如果未优化过则分别对logical / physical m-expr做优化：

对每个logical m-expr，创建O_EXPR task，基于新的search context优化该m-expr
对每个physical m-expr，判断是否满足新context中的property requirement，如果满足则创建O_INPUTS task，对以该physical m-expr作为root的子表达式计算代价

注意这里O_INPUTS是后入栈的，因此会先执行，仍然是为了尽快产生physical plan。

在整个优化流程中，O_GROUP会在2种情况下出现：

初始状态，basic groups中只会有一个logical m-expr，只会产生一个O_EXPR task并入栈，在其执行中生成更多m-exprs
后续，group会以不同的search context被再次优化，这时group中可能已经有一些winners/m-exprs，因此需要有对winner的复用检查和基于新context对m-expr重新优化。

E_GROUP: 扩展一个group

前面介绍rule pattern match时看到，如果对应input group的sub-pattern是一个leaf operator，那总是可以匹配，但如果不是（包含其他operator），则如果想在对应的input group中获取所有binding，需要获取其中的logical m-expr进行比较，这就是E_GROUP task要完成的工作。这里其实是cascades paper中讲述最模糊的地方，但思想很简单，就是在有需要做pattern match时，为了尽可能找到所有rule binding，对input group做exploration，生成所有logical m-exprs。

这里通过标记实现memorization，保证group只被explore一次。另外在代码中，不需要对每个logical m-expr做O_EXPR，只需要对第一个logical m-expr即可。

在cascades paper中，E_GROUP task会创建E_EXPR task，表示对已有logical m-expr应用所有transformation rules，但由于和O_EXPR的工作有重合，columbia中去掉了E_EXPR合并为O_EXPR，通过exploring这个标记表示只做tranform不做implement。

O_EXPR: 优化一个logical m-expr

在columbia中，两种场景会建立O_EXPR task:

O_GROUP task中，需要对目标logical m-expr执行所有的rules（按照promise的顺序），包括基于transformation rule生成新的logical m-expr和基于implementation rule生成physical m-expr。
E_GROUP task中，对group内的logical m-expr执行transformation rule，生成新的logical m-expr做sub-pattern的匹配。

首先要收集rule set中可以fire的rules:

如果已经fire过，不再尝试（unique rule set）
当前是exploring，不尝试implementation rule
top_match做预检查，不匹配的跳过
基于当前context计算promise，只有promise > 0才尝试apply

然后针对排好序后的rules，依次

生成APPLY_RULE task，针对特定rule和特定logical m-expr，以及当前优化context，做具体优化
rule pattern中的input不是leaf operator，则生成E_GROUP task做exploration

注意这里E_GROUP后入栈，因此先深度递归完成了exploration后，再执行APPLY_RULE，task中所有subtree的logical m-exprs已生成，直接查找binding即可。

APPLY_RULE: 具体变换工作

rule总是apply到logical m-expr上，根据rule的类别生成logical/physical m-expr，前面已经讲过基于bindery的基本流程，这里看下伪代码：

首先通过RuleMask避免重复apply。然后循环调用root BINDERY::advance()获取下一个binding。这里还会对rule做一下condition的检查，不满足则不apply，否则调用next_substitute获取新的m-expr并加入search space中：

新生成的是logical m-expr，触发O_EXPR任务，扩展计划空间
新生成的是physical m-expr，触发O_INPUTS任务，完成后续代价计算

O_INPUTS: 获取一个表达式的最优plan

在implementation rule应用后可以得到top operator的具体物理实现，但优化还要递归到所有inputs来获取整个subtree的物理plan，这就是O_INPUTS的工作。它计算每个input group中，针对context的最优physical plan，把cost不断累加，最终得到整个subtree的plan，如果plan cost是针对该context的目前最小值，则记入到winner中。

O_INPUTS也是columbia中应用pruning策略的地方，主要包含2种：

lower bound pruning，前面已介绍过
global epsilon pruning : 当完整优化出一个plan后，如果其cost小于一个预设的上界GLOBAL_EPS，则认为该plan足够优，结束优化流程。很明显这牺牲了plan最优性来提升优化效率，而且对于GLOBAL_EPS的设定会非常困难。

其逻辑伪代码：

在代码中通过Pruning / CuCardPruning / GlobepsPruning 3个标记开启3档剪枝策略：

Pruning就是常规的top-down branch and bounding，用当前累计cost和cost limit比对
CuCardPruning表示开启lower bound pruning，其和Pruning的区别是对尚未优化的group i，InputCost[i]不是0而是group创建时计算的lower bound cost
GlobepsPruning 在完成优化时进行一次判断，如果认为足够优，直接记为winner。

可以看到计算cost的过程是对每个尚未优化过的input group，触发O_GROUP task得到下层最优解并记录在InputCost[]数组中，同时累加到CostSoFar，积极判断CostSoFar > upper bound来做pruning。

当以该physical m-expr为root的plan优化完成后，判断是否search context中的当前最优解，是则替换winner中原最优解。

至此整个search流程就梳理完了，整体还是比较清晰的：

在初始时只有basic groups，每个group中一个initial logical m-expr，和AST中的expr一一对应
开始对top group执行O_GROUP task，其中会对唯一的m-expr调用O_EXPR，生成logical/physical m-exprs，并优先对生成的physical m-expr生成O_INPUTS task，递归下去得到完成的physical plan，并用其cost更新search context中的cost upper bound，帮助后续pruning。
新生成的logical m-expr会继续优化导致一系列m-expr的生成，从而在已有group中扩展新的m-expr或在search space中加入新的group
优化过程中会不断有physical m-expr的生成，然后就递归到下层去生成对应的plan/subplan，并得到各个层次上的局部最优解记入winner中，并返回到上层做汇总，最终回到top group得到完整physical plan
最终top group不再有新的logical / physical m-expr生成时，优化结束，top group winner就是最优plan

如果大家有兴趣可以去看下columbia的代码，由于是实验项目比较简单易懂。

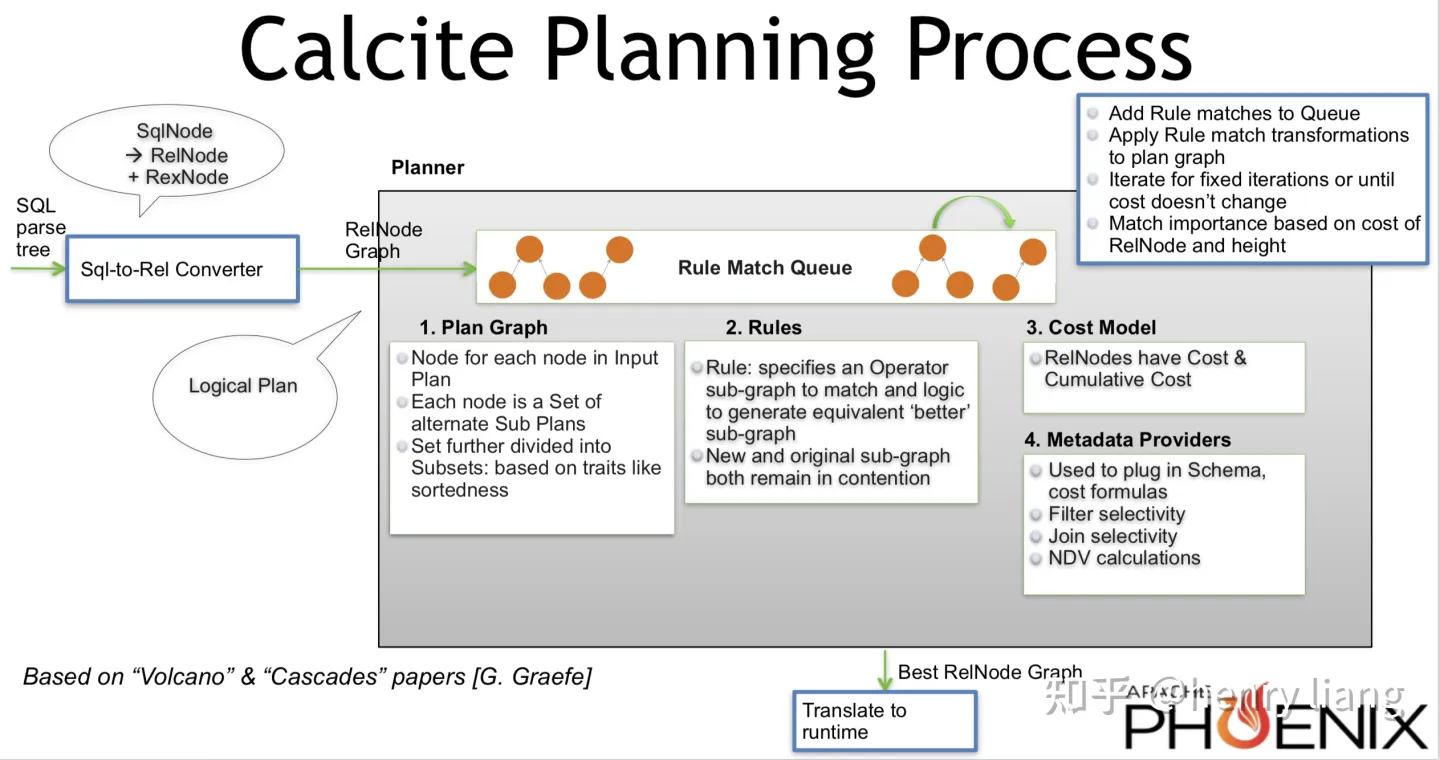
Calcite对cascades的设计参考

Calcite是产业界（尤其大数据领域）应用非常广泛的CBO查询优化器，也是为数不多的基于volcano/cascades的实现。但在粗读其代码和查看一些技术资料后，发现早期版本中的VolcanoPlanner并不是一个严格基于cascades论文的实现，更像其早期原型Exodus的方案。大致来说，就是搜索路径并不具有top-down的规律，而是“随机”落在search space的某个RelNode上。

从代码上看就是对RuleMatch（rule binding）的apply不是以RelSet/RelSubSet为单位从上到下的进行，而是全局共享一个RuleMatch的优先级队列，向其中插入RuleMatch主要在2个时机点：

初始化时调用VolcanoPlanner.setRoot()，设置root RelNode，这会递归触发fireRules，对已有RelNode tree建立一系列RuleMatch，并计算各自的Importance(promise)，进入全局RuleQueue。
在优化过程中生成新的RelNode时，会遍历所有rules，尝试为其建立RuleMatch集合并计算importance，加入RuleQueue。
整个过程持续直到RuleQueue为空或者迭代到目标次数。

这样的好处就是可以通过迭代次数有效限制优化时间，但坏处也非常明显，没有了top-down的路径，无法实现pruning，对于physical property的处理也难以优化。

2020 年 7 月阿里云 MaxCompute（ODPS）团队向社区合并了top-down优化的patch，使得Calcite成为一个真正意义上的cascades优化器，其内部实现就是参考了columbia的设计，并针对Calcite原有流程和结构进行适配，但并没有引入global epsilon pruning的机制。由于作者并不太熟悉Calcite的代码细节，这里就浅尝辄止了，更多介绍可参考

@Eric Fu

大神的这篇文章。

总结

随着大数据的涌现和实时分析需求变得越来越重要，数据库系统对于复杂查询的处理能力逐渐成为武器库的基本装备，作为执行计划的生成组件，优化器的功能性会对系统的计算能力产生质的影响。

cascades框架是理论上最为灵活且扩展性最强的优化器实现方案，但可惜目前业界成熟的实现并不多，开源的更少。

Calcite虽然广为使用但其自身主要针对异构数据源的兼容，在优化规则的支持上并不很丰富
Orca虽然强大，但由于与Postgres生态的耦合较深，导致无法被广泛应用
CockroachDB的优化器虽然也采用cascades，但主要集中在heuristic上，cost based的部分较少
最为成熟的应该是G. Graefe主导的SQL Server optimizer，可惜不开放…

看起来最值得研究的还是GPOrca，后续笔者争取能写一些关于Orca的设计实现和代码分析文章，敬请期待。

今天的文章capcom优化好_cpu优化器分享到此就结束了，感谢您的阅读。

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容，请发送邮件至举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/85204.html