「自控原理」3.1 时域分析法、一阶系统时域分析

本节介绍时域分析法、典型输入信号、常用性能指标
本节介绍一阶系统的时间响应和动态性能指标

概述

以下讲解，均针对线性系统。

时域法

时域法，即时域分析法（也称时间响应法）。是最基本的分析方法。
所谓时域就是信号都是时间t的函数。
在时域进行分析，即以时间为独立变量，对系统施加某一典型输入信号，研究系统的输出时间响应来分析和评价系统的性能。
根据自动控制系统稳准快的要求，时域分析法需要分析其稳定性、稳态误差、暂态响应。
在时间域中对系统进行分析校正，直观准确。且时域分析可以提供系统时间响应的全部信息。缺点是求解比较繁琐。

时间响应

系统的时间响应即描述系统的微分方程的解
通过拉氏变换可以较方便地解微分方程


以上推导为了形式简洁并未涉及D(s)有重根或共轭复根的情况。遇到了正常按照拉氏变换求就可以。

一般研究的是零状态响应，此时第三项为0。
第一项中$s_i$是传递函数的极点，系统稳定的情况下，这一项会随时间衰减至0，因此称其为暂态分量。第二项中$s_j$只与外界输入有关，不随时间衰减，因此这一项为稳态分量。
当系统稳定时，暂态分量也称作暂态响应。（系统不稳定时就没有暂态稳态之分了，自然也没有暂态响应的概念了）
稳态响应一般是指强迫响应。

四个常用的典型输入信号

研究系统只需要研究其在某些典型输入信号下的响应，即可通过卷积运算得到系统在任何输入下的输出。
而且在同样的典型信号下研究响应，有利于对系统性能进行对比。

单位脉冲函数
单位脉冲是对脉冲宽度足够小的实际脉冲函数的数学抽象。可以用于考察系统在脉冲扰动后的恢复特性。
举例如撞击、后坐力、电脉冲等。
单位阶跃函数
单位阶跃函数用于考察系统对于一个突然变化以及恒值信号的跟踪能力。
单位阶跃响应往往作为系统动态性能指标评价的基础。通常以单位阶跃信号作为典型输入。
举例如开关量。
单位斜坡函数
单位斜坡函数用于考察系统对匀速输入信号的跟踪能力。
单位加速度函数
单位加速度函数用于考察系统的机动跟踪能力

典型输入信号之间的关系

从单位加速度到单位斜坡到单位阶跃到单位脉冲，是微分关系。对应像函数每次×s。
注意：对于线性定常系统，虽然输入不同信号，对应的输出响应不同，但它们所表征的系统性能是一致的

五个常用的性能指标

在保证系统稳定的前提下，控制系统的优劣在于系统的调节能力。也就是当外界输入发生变化时，系统是否及时作出响应。
一般认为，阶跃输入是最严峻的一种工作状态，因此通常用单位阶跃响应的特征量来描述系统的动态性能。
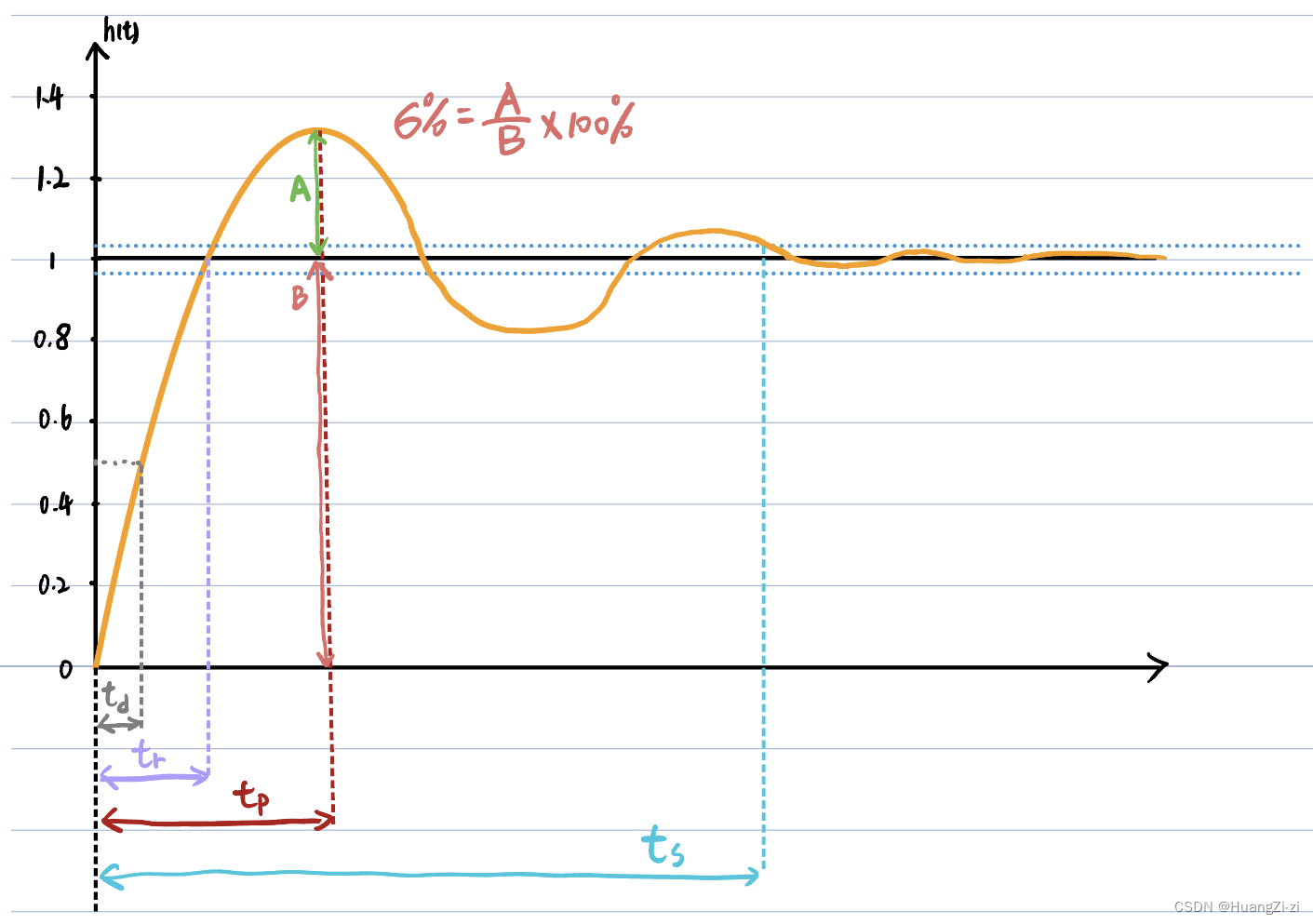
假设系统的单位阶跃响应如图所示：

一般来说，误差带取5%

这5个性能指标中：
上升时间T_r越短，说明系统响应速度越快
峰值时间T_p越短，说明系统反应越灵敏

关于调节时间T_s，在工程实践中，往往并不使用以上的定义。而是采用单位阶跃响应曲线的包络线到达并保持在终值误差带内所需的最短时间。因为在有震荡的情况下，如果看响应曲线，则调节时间变得不连续，不方便进行研究。因此使用包络线来近似。（这一点将在后面中探讨）

一阶系统的时间响应及动态性能

一阶微分方程描述的系统称为一阶系统。反映在传递函数上就是闭环传递函数分母为s的1次方程。比较典型的例子是RC串联电路。

一阶系统传递函数的标准形式

一阶系统的典型传递函数为$\frac{1}{Ts+1}$

单位阶跃响应

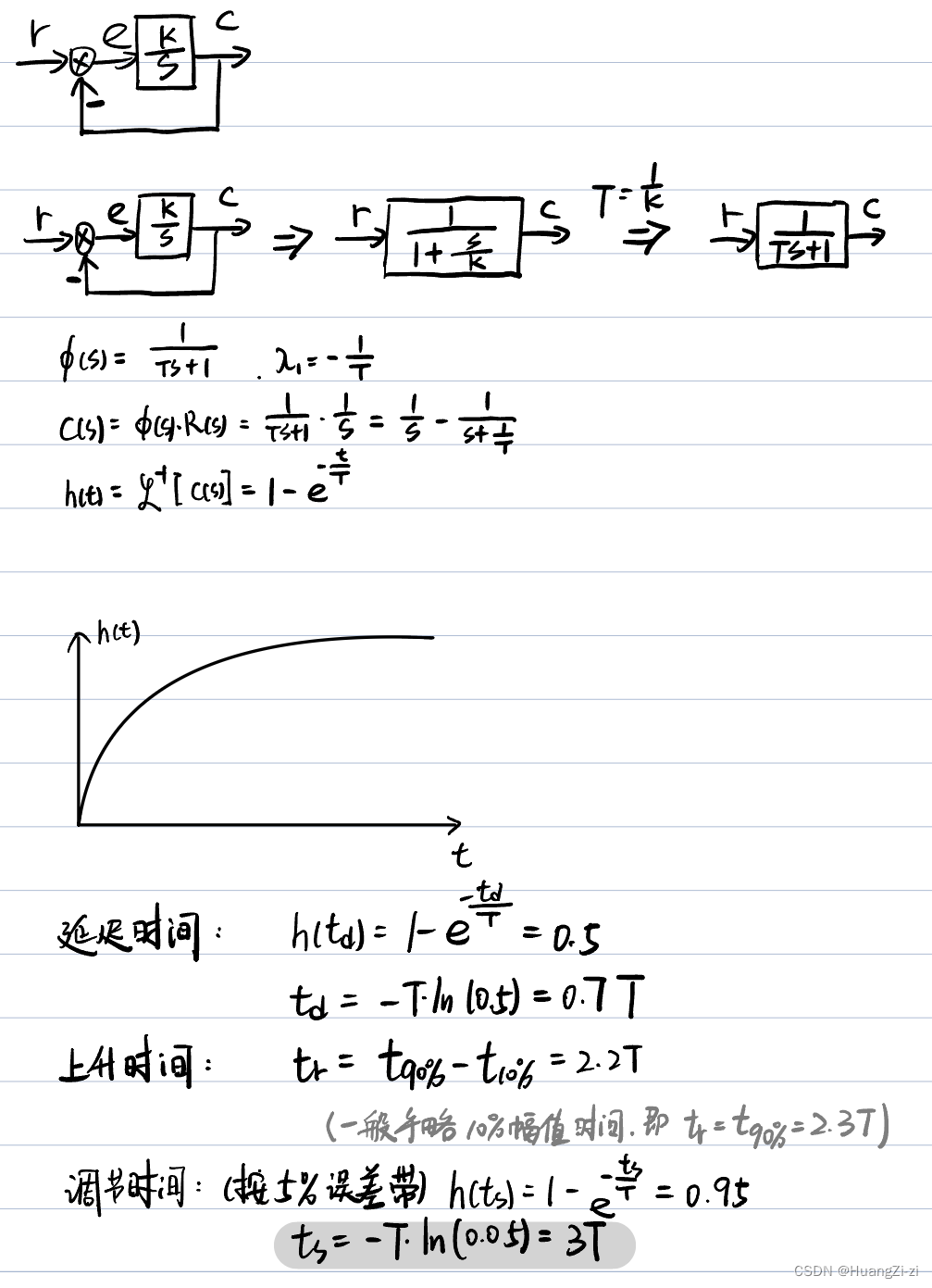
构建单位反馈系统，并研究其输出：

时间响应：$h(t)=1-e^{-\frac{t}{{}_T}}$
因为没有超调，所以也就没有峰值时间和超调量这两个指标。
动态性能指标：
$t_s=3T(\delta =5\%y(\infty ))$
$t_s=4T(\delta =2\%y(\infty ))$
其他的了解就行

其他典型响应

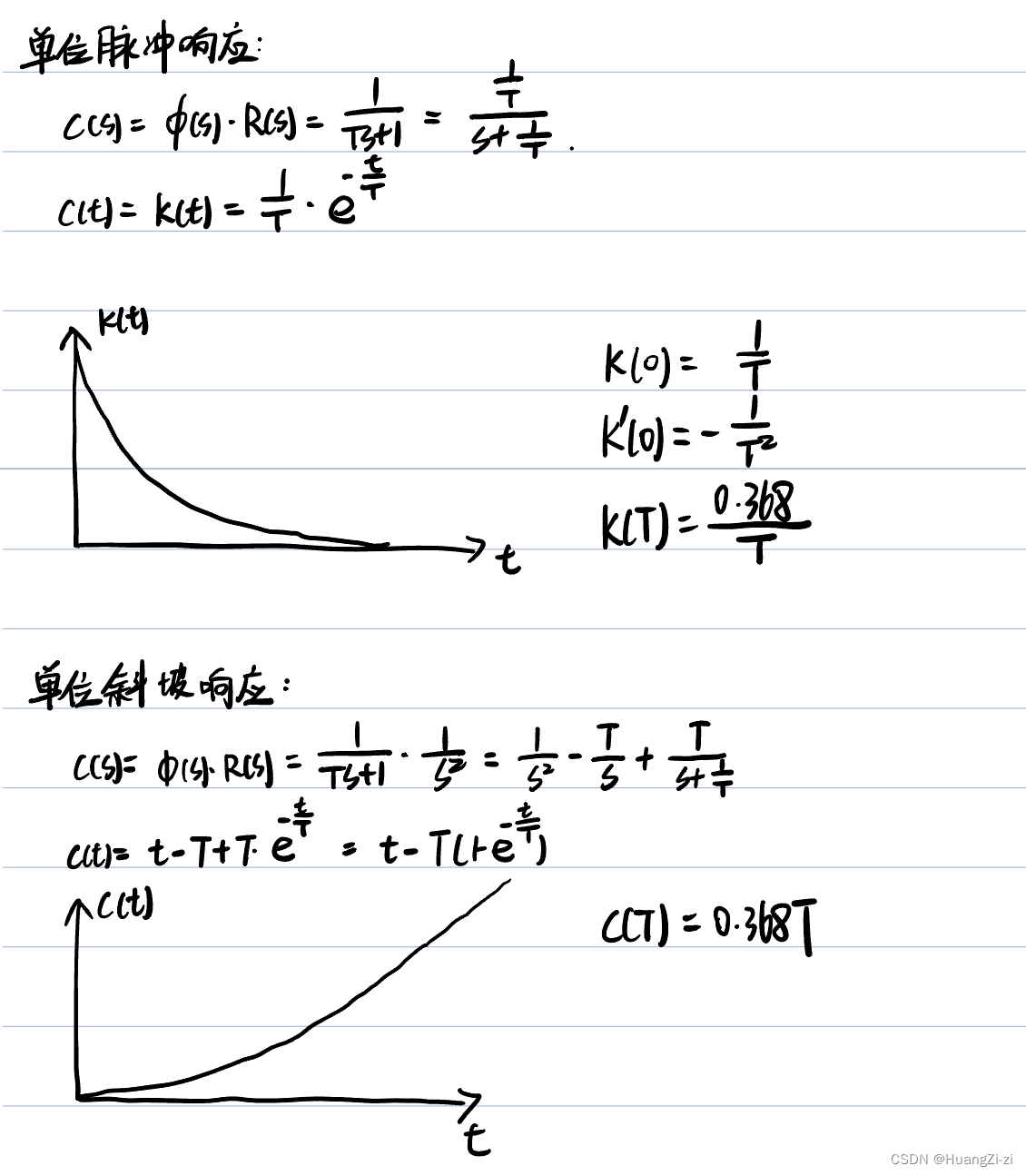
除了单位阶跃响应以外，单位脉冲响应、单位斜坡响应也是典型响应
其他典型响应满足：对积分的响应=对响应的积分，也就是输入信号满足积分关系，响应信号也满足积分关系

这两个了解一下就好。如果让计算那么按照定义去计算相应的性能指标就可以了。
单位脉冲响应有专属的字母k(t)来表示
单位阶跃响应的专属字母是h(t)

例题

这个地方要注意多使用各个传递函数之间的关系，第一是单位阶跃响应和单位脉冲响应的微分关系。第二是开环传递函数和闭环传递函数的反馈等效关系。

今天的文章「自控原理」3.1 时域分析法、一阶系统时域分析分享到此就结束了，感谢您的阅读。