【机器学习－西瓜书】八、集成学习：结合策略；多样性；总结「建议收藏」

推荐阅读： 总结；绝对多数投票法；误差-分歧分解

8.4 结合策略

关键词：平均法；投票法；学习法;硬投票；软投票

一开始就说到，集成学习有两个关键，第一，个体学习器；第二，结合策略。对于个体学习器，通常分串行（boosting）和并行（bagging）的方法构建。有了一组学习器，如何把它们结合起来使用呢？这就设计到结合策略，通常有：简单平均法；投票法；学习法。

8.4.1 平均法
对于数值输出（回归？）问题，常见的就是平均法（averaging）.通常有简单平均法： $H(x)=\frac{1}{T}\sum _{i=1}^{T}h_{i}(x)$ 以及加权平均法： $H(x)=\sum _{i=1}^{T}w_{i}h_{i}(x)$ 。加权平均法的权重是从训练数据中学习而得，在现实任务中的训练样本通常不充分或存在噪声，使得学习的权重不一定可靠。因此，一般地在个体学习器性能相差较大时宜采用加权平均法，而在个体学习器性能相近时使用简单平均法。

8.4.2 投票法

对于分类问题，常用投票法（voting）。常见有三种投票法：
1.绝对多数投票法（majority voting）：

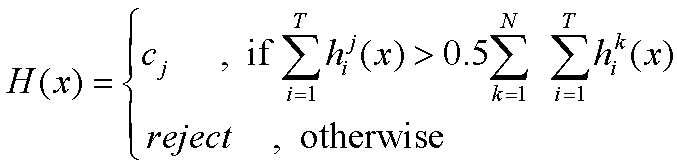
其中，T表示有T个分类器，N表示有N种类别。意思就是，T个分类器对类别j的预测结果若大于总投票结果的一半，那么就预测是类别j，否则就拒绝预测。
2.相对多数投票法（plurality voting）：即得票最多的那个类别为预测类别。
3.加权投票法（weighted voting）
在分类任务中，不同类型的个体学习器产生不同类型的。通常有两种，一个是类标记,如，决策树，使用类标记的投票称为硬投票（hard voting）；一个是类概率，如贝叶斯分类器，使用类概率的投票称为软投票（soft voting）

8.4.3 学习法
学习法顾名思义，最终的输出是把个体学习器的输出输入到一个学习器，最终得到预测结果。

8.5多样性

关键词：误差-分歧分解；多样性度量；k-误差图

8.5.1误差-分歧分解

再一次重温一下，集成学习两个关键，第一，个体学习器；第二，结合策略。而一组个体学习器的关键是“好而不同”，也就是要有差异性而且还要性能好，那我们如何衡量个体学习器之间的差异性呢？有什么指标吗？指标是有的。

针对回归任务而言，有误差-分歧分解，误差-分歧中的分歧表征了个体学习器在样本x上的不一致性，即一定程度反映了个体学习器的多样性。
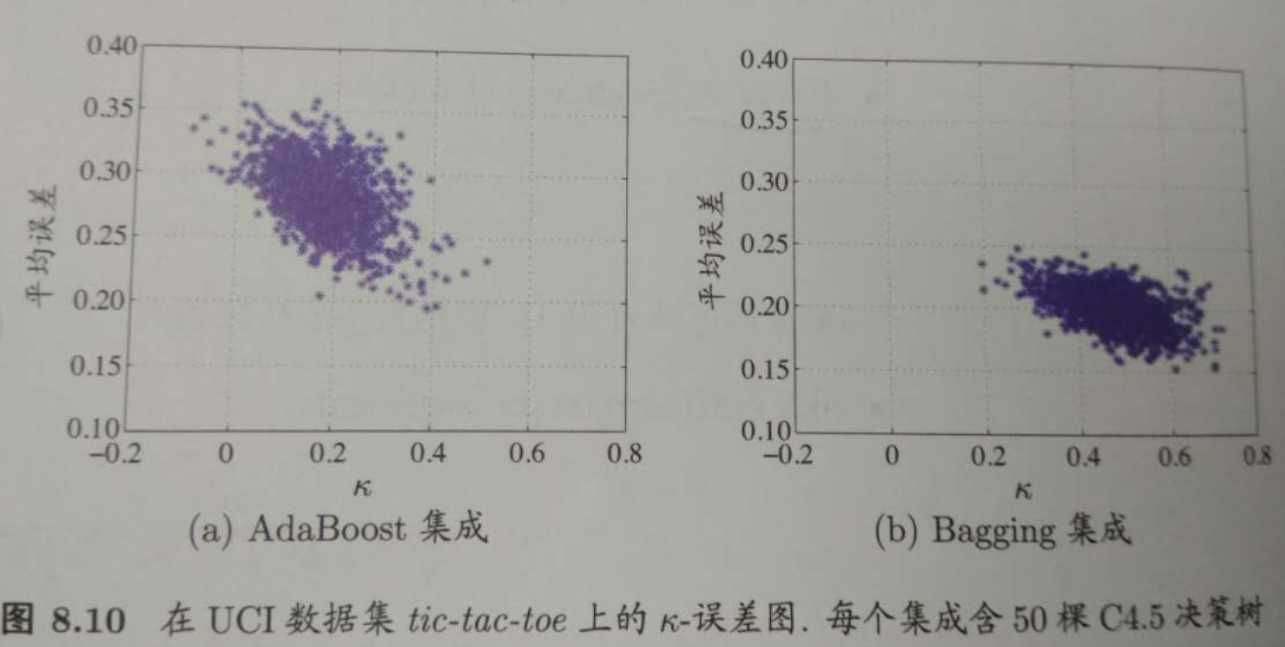
针对分类任务，有多样性度量（diversity measure），典型做法是考虑个体分类器的两两相似/不相似性。画出两个分类器的预测结果列联表（contingency table），类似于混淆矩阵的一个东西。通过这个联表，可以得出一个叫k-统计量（k-statistic）的东西，再计算平均误差，即可得到k-误差图。k-误差图横轴是k值，纵轴是它们的平均误差。显然，数据点云的位置越高，个体分类准确性越低；位置越靠右，个体学习器多样性越小。

增强多样性的方法有：数据样本扰动；输入属性扰动；输出扰动；算法参数扰动

1.数据样本扰动，就是8.2节中讲的 boosting 和bagging，这种方法对“不稳定学习器”（例如，决策树，神经网络）很有效。对于稳定基学习器（stable base learner），如线性学习器，支持向量机，朴素贝叶斯，KNN，往往使用输入属性扰动。
2.输入属性扰动，训练样本通常由一组属性描述，不同的“子空间”提供了观察数据的不同视角。显然，从不同子空间训练出的个体学习器必然有所不同。子空间一般指从初始的高维属性空间投影产生的低维属性空间。
3. 输出表示扰动，例如翻转法（Flipping Output），随机改变一些训练样本的标记；也可对输出表示进行转化，如“输出调制法”（Output Smearing）
4. 算法参数扰动