前情提要
绪论 (一) 振动力学的基本概念
绪论 (二) 振动力学的基本问题与基本方法
什么是简谐振动?
简谐振动 系统的运动参量(位移、速度、加速度等) 按时间的正弦或余弦函数规律变化的振动
为什么学习振动从学习简谐振动开始?
首先是因为简谐振动简单,其次是因为任何周期振动都可以分解为不同阶次简谐振动的叠加运动。先搞明白简谐振动,再学会如何分解周期振动,我们实际上就掌握了分析所有周期振动的方法。
简谐振动有三样写法,你知道吗?
简谐振动的三角函数表示法
位移表达式 (余弦形式) x ( t ) = X cos ( ω t + φ 0 ) (1) x(t)=X\cos(\omega t+\varphi_0)\tag{1} x(t)=Xcos(ωt+φ0)(1)
- 式中 X X X 为振幅, ω \omega ω 为圆频率, t t t 为时间, φ 0 \varphi_0 φ0 为初相位
- 用正弦形式 x ( t ) = X sin ( ω t + φ 0 ′ ) x(t)=X\sin(\omega t+\varphi_0′) x(t)=Xsin(ωt+φ0′) 表达也行,但同一个简谐振动,正弦和余弦形式表达式的初相位有区别
- 振幅 X X X 和初相位 φ 0 \varphi_0 φ0 由初始条件确定
速度表达式 (位移对时间求一阶导数可得)
v = d x d t = − X ω sin ( ω t + φ 0 ) = X ω cos [ ( ω t + φ 0 ) + π 2 ] (2) v=\frac{\text{d}x}{\text{d}t}=-X\omega\sin(\omega t+\varphi_0)=X\omega\cos{\left[ \left( \omega t+{
{\varphi }_{0}} \right)+\frac{\pi }{2} \right]} \tag{2} v=dtdx=−Xωsin(ωt+φ0)=Xωcos[(ωt+φ0)+2π](2)
加速度表达式 (位移对时间求二阶导数可得)
a = d 2 x d t 2 = − X ω 2 cos ( ω t + φ 0 ) = X ω 2 cos [ ( ω t + φ 0 ) + π ] (3) a=\frac{\text{d}^2x}{\text{d}t^2}=-X\omega^2\cos(\omega t+\varphi_0)=X\omega^2\cos{\left[ \left( \omega t+{
{\varphi }_{0}} \right)+\pi\right]} \tag{3} a=dt2d2x=−Xω2cos(ωt+φ0)=Xω2cos[(ωt+φ0)+π](3)
简谐运动的运动学特征
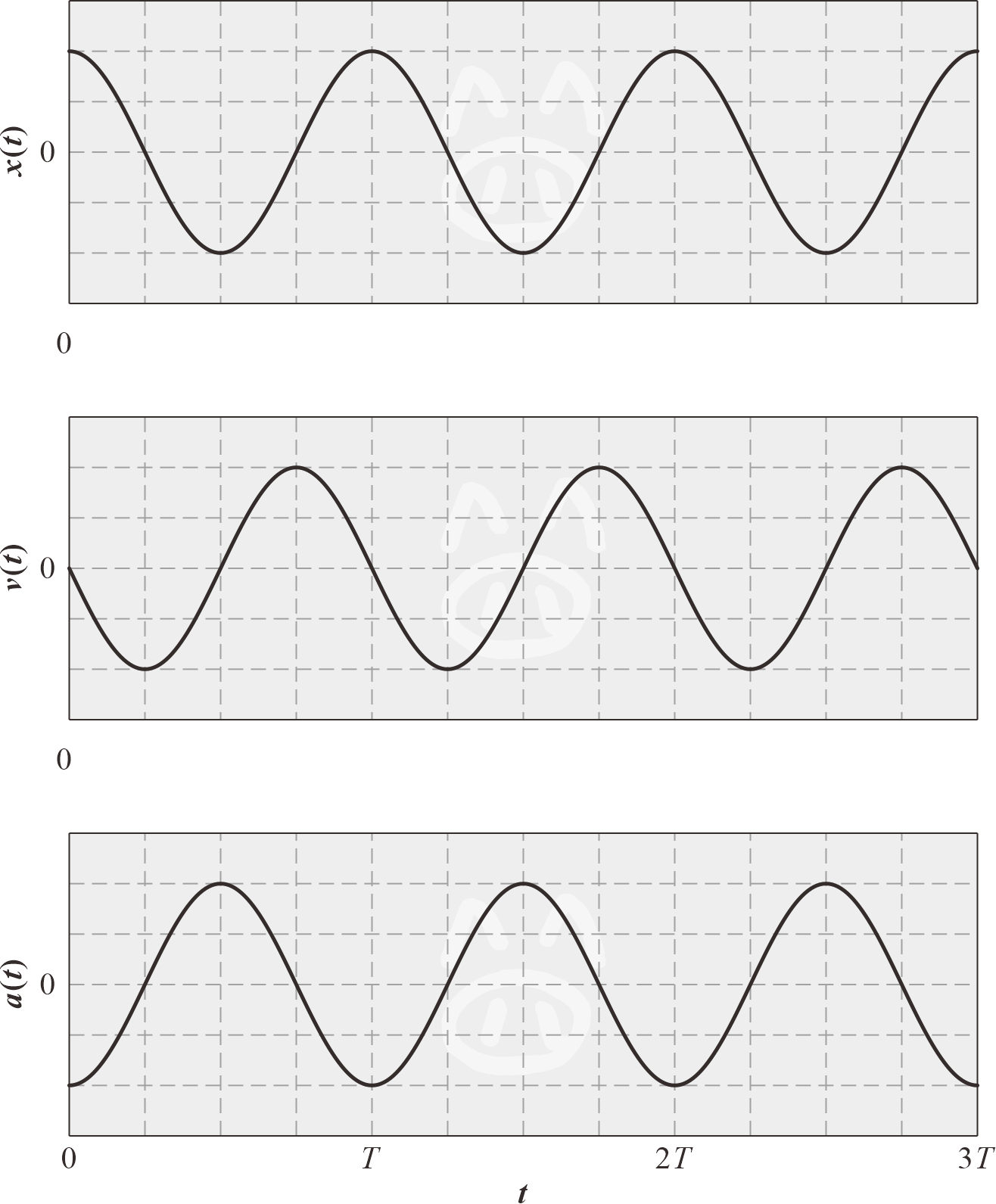
- 简谐振动的速度和加速度也是简谐函数,且位移、速度和加速度的频率相同;
- 较之位移的相位,速度相位超前 π / 2 \pi/2 π/2,加速度相位超前 π \pi π;
- 加速度和位移恒成正比但方向相反,位移越大处加速度也越大。比例系数为圆频率 ω \omega ω 的平方。
图1 简谐振动的位移、速度、加速度时程曲线
简谐振动的矢量表示法
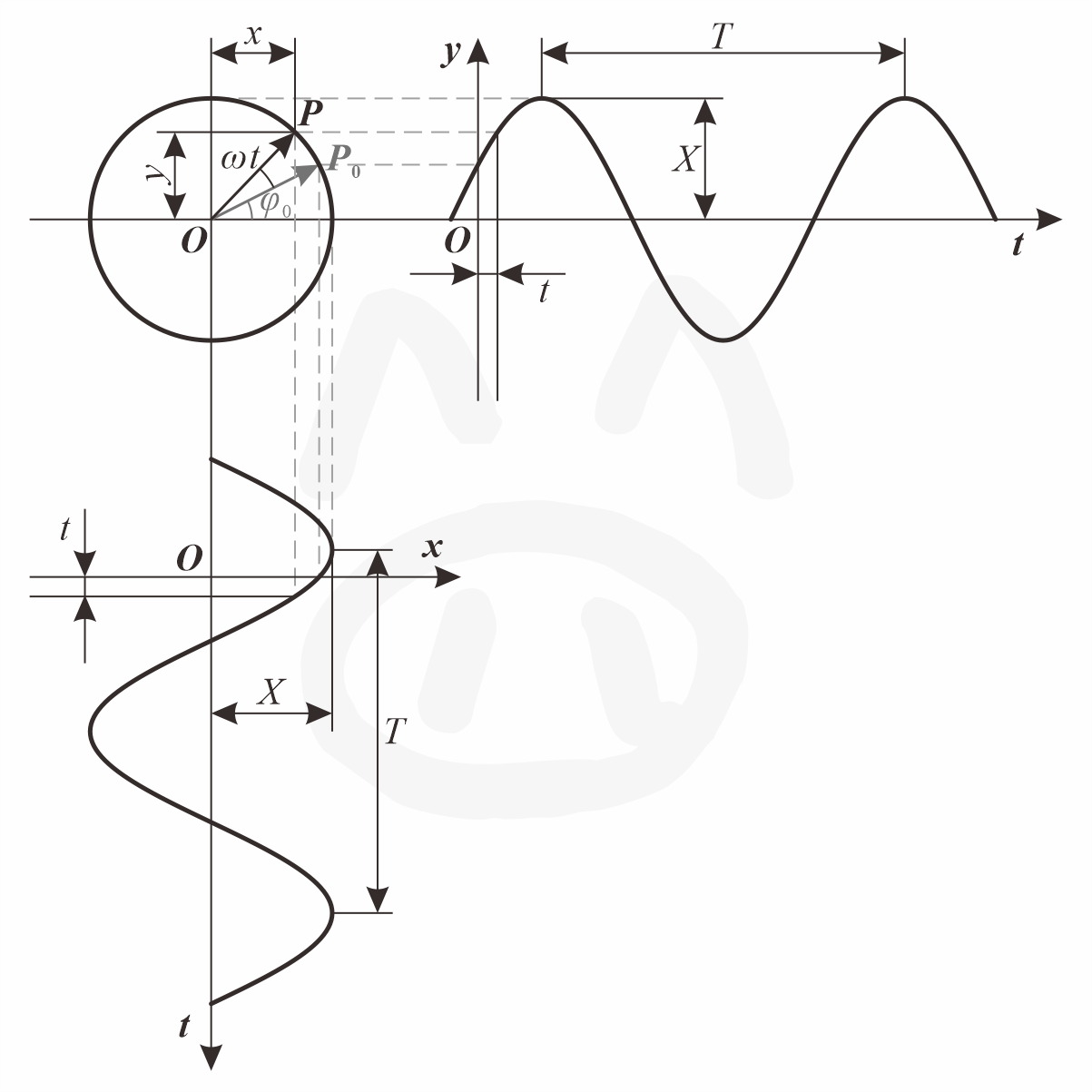
用旋转矢量 O P ⇀ \overset{\rightharpoonup}{OP} OP⇀ 在坐标上的投影表示。 O P ⇀ \overset{\rightharpoonup}{OP} OP⇀ 的:
- 模 为简谐振动的 振幅 X X X
- 与水平轴正方向的夹角 为简谐振动的***相位角 ω t + φ 0 \omega t+\varphi_0 ωt+φ0,其中 t = 0 t=0 t=0 时与水平轴正方向的夹角为简谐振动的 初相位角
- 旋转角速度 为简谐振动的圆频率 ω \omega ω
- 在横坐标上的投影 x ( t ) = X cos ( ω t + φ 0 ) x(t)=X\cos(\omega t+\varphi_0) x(t)=Xcos(ωt+φ0) 与式 ( 1 ) (1) (1) 相同,可见旋转矢量简谐振动存在一一对应的关系,可以用旋转矢量来表示简谐振动
- 在纵坐标上的投影 y ( t ) = X sin ( ω t + φ 0 ) y(t)=X\sin(\omega t+\varphi_0) y(t)=Xsin(ωt+φ0) 也可以用来表示简谐振动,其与横坐标投影所表示的简谐振动幅值、频率都相同,但相位落后 π / 2 \pi/2 π/2
图2 简谐运动的矢量表示法
简谐振动的复数表示法
数学基础:欧拉公式
Z = A ( cos θ + i sin θ ) = A e i θ R e ( A e i θ ) = A cos θ I m ( A e i θ ) = A sin θ (4) \begin{align} &Z=A(\cos \theta +i\sin \theta )=A{
{e}^{i\theta }} \\ &Re(A{
{e}^{i\theta }})=A\cos \theta \\ &Im(A{
{e}^{i\theta }})=A\sin \theta \\ \end{align} \tag{4} Z=A(cosθ+isinθ)=AeiθRe(Aeiθ)=AcosθIm(Aeiθ)=Asinθ(4)用欧拉公式表示式 ( 1 ) (1) (1) 所示的简谐振动: x ( t ) = X cos ( ω t + φ 0 ) = R e [ X e i ( ω t + φ 0 ) ] = R e ( X e i φ 0 e i ω t ) x\left( t \right)=X\cos \left( \omega t+{
{\varphi }_{0}} \right) =Re\left[ X{
{e}^{i\left( \omega t+{
{\varphi }_{0}} \right)}} \right]=Re\left(Xe^{i\varphi_0}e^{i\omega t}\right) x(t)=Xcos(ωt+φ0)=Re[Xei(ωt+φ0)]=Re(Xeiφ0eiωt)
简谐振动的复数表达式 (振动分析中可以省略实部或虚部符号) x ( t ) = X e i φ 0 e i ω t = X ˉ e i ω t (5) x\left( t \right)=Xe^{i\varphi_0}e^{i\omega t}=\bar{X}e^{i\omega t}\tag{5} x(t)=Xeiφ0eiωt=Xˉeiωt(5)
- 复振幅 X ˉ = X e i φ 0 \bar{X}=Xe^{i\varphi_0} Xˉ=Xeiφ0
数学基础:复变函数的运算
Z 1 = A 1 e i θ 1 , Z 2 = A 2 e i θ 2 Z_1=A_1e^{i\theta_1},Z_2=A_2e^{i\theta_2} Z1=A1eiθ1,Z2=A2eiθ2幂 Z n = A n e i n θ (6) Z^n=A^ne^{in\theta}\tag{6} Zn=Aneinθ(6)乘积 Z 1 Z 2 = A 1 A 2 e i ( θ 1 + θ 2 ) (7) \\Z_1Z_2=A_1A_2e^{i\left(\theta_1+\theta_2\right)}\tag{7} Z1Z2=A1A2ei(θ1+θ2)(7)商 Z 1 Z 2 = A 1 A 2 e i ( θ 1 − θ 2 ) (8) \\\frac{Z_1}{Z_2}=\frac{A_1}{A_2}e^{i\left(\theta_1-\theta_2\right)}\tag{8} Z2Z1=A2A1ei(θ1−θ2)(8)
参考文献
[1] 鲍文博,白泉,陆海燕.振动力学基础与MATLAB应用[M].北京:清华大学出版社,2015:6~7.
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/87799.html