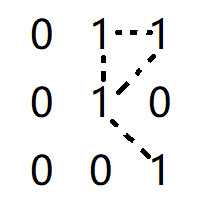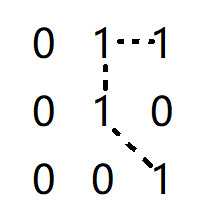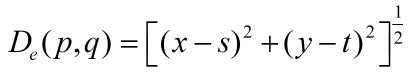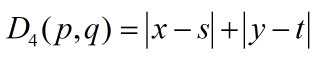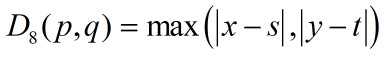冈萨雷斯：数字图像处理第二章学习笔记

取样和量化
一幅图像的x和y坐标及幅度可能都是连续的。为了将它转换成数字形式，必须对坐标和幅度都进行取样操作。对坐标进行数字化成为取样，对幅值数字化成为量化。
饱和度
饱和度是指超过这个值的灰度级将被剪切掉的一个最高值。
噪声
对比度
将一幅图像中最高和最低灰度级间的灰度差定义为对比度。
4邻域，对角邻域和8邻域
三种邻域的符号如下：

其中，4邻域的坐标为：
(x+1, y), (x-1, y), (x, y+1), (x+1, y-1)
对角邻域的坐标为：
(x+1, y+1), (x+1, y-1), (x-1, y+1), (x-1, y-1)
8邻域就是4邻域和对角邻域的并集。
下面图片会更清晰解释邻域：
定义邻接性的灰度值集合V
引用原文的一句话：令V是用于定义邻接性的灰度值集合。在二值图像中，如果把具有1值的像素归诸于邻接像素，则V={1}。
这句话我是这么理解的：在二值图像中，只有两种像素点值 0 和 1。我们现在研究的是像素值为1的像素点的邻接，此时V={1}。一定要注意，V是灰度值的集合，不是像素点的集合。也就是说，V的元素只有一个，不是一张图像中像素值为1的所有点。在一张二值图像中，任何一个像素点如果像素值为1，那么该点的像素值就来自V。
打个不太确切的比方，有两种肤色的人种——黑色人种和白色人种，我们现在要考察黑色人种在地球上的分布，那么我们现在就是研究黑色人种的分布，所以V={黑色人种}，注意V只有一个元素，不是所有黑色人种的集合。调查时发现了一个黑色人种，就可以说他是来着V中的属性的人。
在灰度图像中，概念是一样的，但是集合V一般包含有更多的元素。例如，灰度值范围为0到255的邻接像素中，集合V可能是这个256个值得任何一个子集。
4邻接，8邻接和m邻接
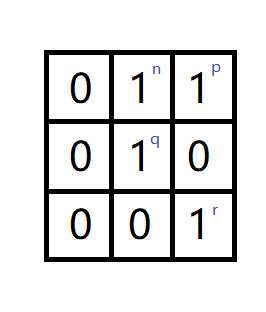
1） 4邻接。如果 q 在集合 p 的4邻域中，则 p 与 q 是4邻接的。即 q 所在像素点为上述图片的四个红色方框之一时 p 与 q 是4邻接的。
2） 8邻接。如果 q 在集合 p 的8邻域中，则 p 与 q 是8邻接的。即 q 所在像素点为上述图片的四个红色方框之一或者四个黑色方框之一时 p 与 q 是8邻接的。
3） m邻接，又称混合邻接。两种情况为 m 邻接。
第一，如果 p 与 q 是4邻接，则 p 与 q 是 m 邻接的。
第二，如果 p 与 q 是8邻接，且 p 的4邻域和 q 的4邻域的交集中没有来自V中数值的像素，则 p 与 q 是 m 邻接的。
混合邻接时8邻接的改进，混合邻接的引入是为了消除采用8邻接时产生的二义性。举个例子会更好理解，就拿书本的例子来详细说明。

如果将图中有着8邻接的像素点用一条虚线连接，得到如下结果：

可以看到像素点p和像素点q之间存在两条通路，即存在着多重（二义性）8邻接。如果考虑 m 邻接，则可以消除该二义性。考虑图中的 m 邻接，显然 p 与 n，n 与 q 之间有着 m 邻接，因为这两组像素点符合 m 邻接的第一种情况。接着来分析 p 与 q，q 与 r 之间是否具有 m 邻接，这两组像素点显然不符合第一种情况，所以分析是否符合第二种情况。
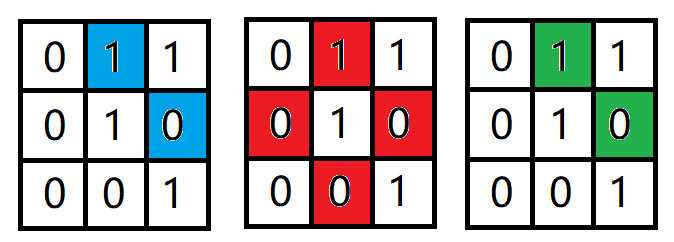
先来看 p 与 q，p 与 q 的4邻域的像素点如下，其中蓝色为 p 的4邻域（图像外的未标出），红色为 q 的4邻域。显然，绿色的即为 p 与 q 的4领域的交集。

标为绿色的像素点中，有一个像素值为1，是来自V中数值的像素，所以 p 与 q 不是 m 邻接。同理分析得 q 与 r 是 m 邻接。如果将图中有着 m 邻接的像素点用一条虚线连接，得到如下结果：

这就消除了二义性。
距离向量
对于坐标分别为(x, y), (s, t), (v, w)的像素 p，q，z。
p 与 q 的欧几里得距离定义如下：

p 与 q 的距离D_4(城市街区距离)定义如下：

p 与 q 的距离D_8（棋盘距离）定义如下：