1.何为特勒根定理
预备知识:关联矩阵A的定义,基尔霍夫定律的基本回路表示形式
①单电路某一时刻
对于一个有b条支路,n个节点的集中参数电路,选取各支路电路方向和电压方向为一致参考方向,则在某一时刻
(1)
其物理意义就是对于电路来说,任一时刻吸收或发出的总功率为0,即功率守恒
推导过程如下:
②单电路不同时刻
在上面的推导过程中,将条件弱化为两个时刻t1和t2,不难得出具有相同规律
③不同电路不同时刻
对于具有相同拓扑结构的电路A、B,其有向图具有相同的结构,即关联矩阵A相同
因此惊奇地发现,仍然满足
但②③中这种乘积形式并不具有真正的功率意义,因此也可以称为似功率,那么特勒根定理就是(似)功率守恒定理,这个定理是由电路的内禀性质所决定的,与时间、空间无关。
2.黑箱问题
看下面这道例题,中间的N只有电阻构成,题目给出同一电路不同时刻的相关电路数据,我们可以考虑采用特勒根定理②解决此类问题
对于两个状态,写出特勒根方程
这里需要注意,对于N里面若干各电阻,也就是Σ对应的那两项是相同的,因此上下联立可以给出
其中的u1、u2用欧姆定律计算解得
今天的文章 特勒根定理的原理和典型应用[通俗易懂]分享到此就结束了,感谢您的阅读。



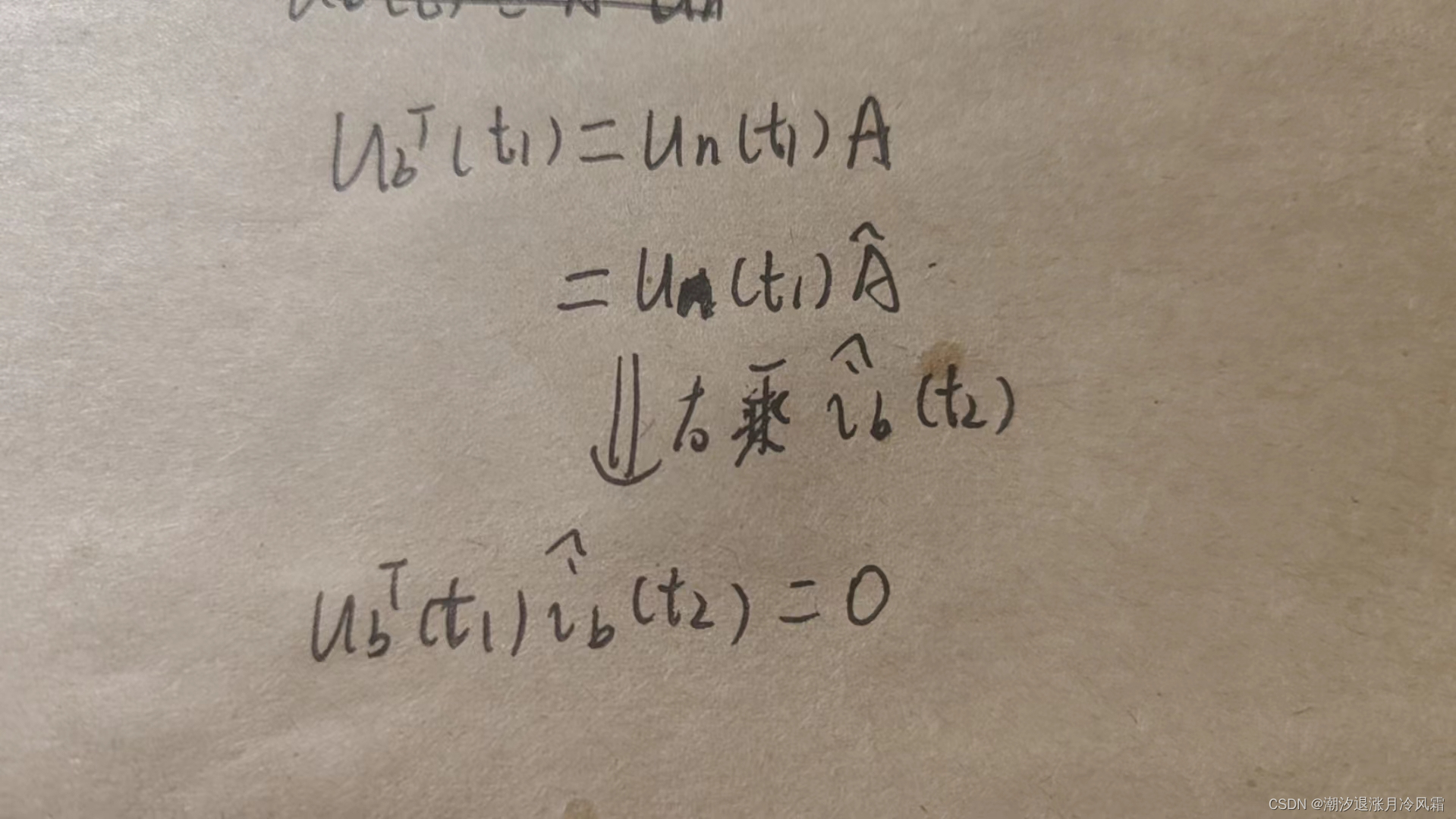

版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/bian-cheng-ji-chu/103091.html