凸集和凸优化
一、 凸集
1. 凸集与仿射集的关系
- 说道凸集,就不得不提到仿射集的概念。
- 仿射集:
- 通过集合C中任意两个不同点的直线仍在集合C内,则称集合C为仿射集(例如直线和平面)。

- 设X1和X2是定义在集合C中任意两个不同的点,即X1 ≠ X2,并且 X1,X2 ∈ C,θ⊆R,对θ都有θX1 + (1-θ)X2 ∈ C,则称C为一个仿射集。
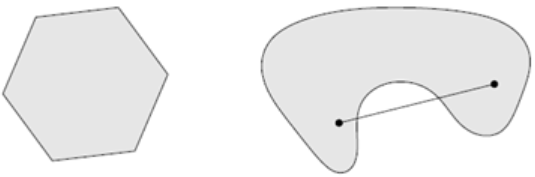
- 若对上面定义增加一个条件0 ≤ θ ≤1,则C为一个凸集。
- 因为仿射集的条件比凸集的条件强,因此仿射集必然是凸集。
- 通过集合C中任意两个不同点的直线仍在集合C内,则称集合C为仿射集(例如直线和平面)。
2. 凸集相关概念
- 保凸运算:
1.凸集与凸集的交集还是凸集;
2.仿射变换,即线性变换;
3.透视变换;
4.投射变换。 - 保凸算子:
- 凸函数的非负加权和
- 凸函数和仿射函数的复合
- 凸函数的逐点最大值,逐点上确界
f(x) = max( f1(x),f2(x),fk(x)…fn(x) )
f(x) = sup g(x,y)
二、凸函数
1. 定义
- 若一个函数满足:
1.定义域是凸集
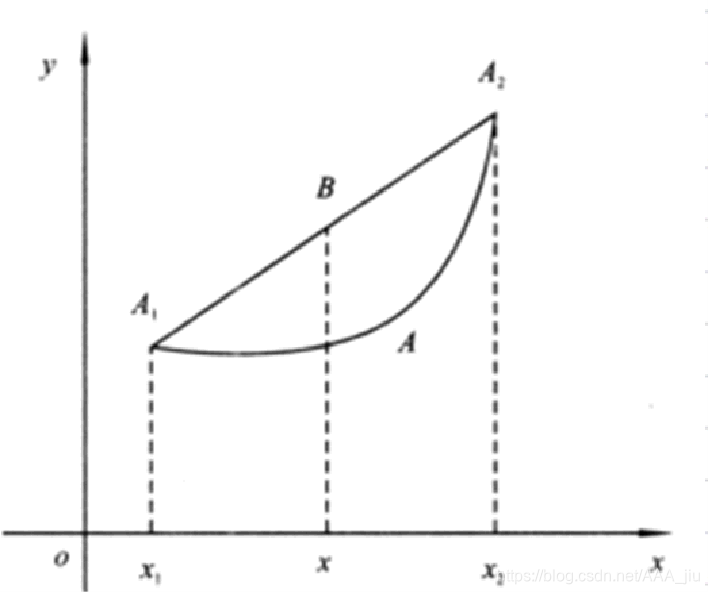
2.f(ax1 + (1-a)x2) <= af(x1) + (1-a)f(x2) 其中:∑a1=1,a1 >= 0 那么该函数为凸函数。
示例: f ( x 1 + x 2 2 ) ≤ f ( x 1 ) + f ( x 2 ) 2 f(\frac {x_1+x_2}{2})≤\frac {f(x_1)+f(x_2)}{2} f(2x1+x2)≤2f(x1)+f(x2)

2. 性质
- 凸函数的局部极小值就是全局最小值
- 凸函数Hessian矩阵半正定
- Q为半正定对称阵,f(x) = xTQx为凸函数
- f(x)为凸函数,f(E(x)) <= E(f(x)) (Jesson不等式)其中E(x)是x的期望
Hessian矩阵半正定:- 特征值:向量变换的大小;
3. 凸函数举例
- 指数函数f(x) = ex
- 幂函数f(x) = xa
- 负对数函数f(x) = -logx
- 负熵函数f(x) = xlnx
- 范数f(x) = ||x||
- 最大值函数f(x) = max(x1,x2,…,xn)
4. 海森矩阵
4.1 海森矩阵(Hession)和极值的关系
- 可导函数在某一点处取得极值的必要条件是梯度为0,梯度为0的点成为函数的驻点这是疑似极值点。需要注意的是,梯度为0只是函数取极值的必要条件而不是充分条件,即梯度为0的点可能不是极值。
如果Hession矩阵正定(所有特征值为正数),函数有极小值;
如果Hession矩阵负定(所有特征值为负数数),函数有极小值;
如果Hession矩阵不定(所有特征值为有正有负),则不是极值点(鞍点)。
5. 泰勒展开式
5.1 定理
- 设n是一个正整数,如果定义在一个包含a的区间上的函数f在a点处n+1次可导,那么对于这个区间上的任意x,都有:
f ( x ) = f ( a ) + f ′ ( a ) 1 !

版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/bian-cheng-ji-chu/104886.html