文章目录
多属性决策模型主要针对数学建模问题中的一些小的子问题进行求解,如果想直接使用请跳转至——四、五
视频回顾
一、算法介绍
多属性决策是现代决策科学的一个重要组成部分,它的理论和方法在工程设计、经济、管理和军事等诸多领域中有着广泛的应用,如:投资决策、项目评估、维修服务、武器系统性能评定、工厂选址、投标招标、产业部门发展排序和经济效益综合评价等.
多属性决策的实质是利用已有的决策信息通过一定的方式对一组(有限个)备选方案进行排序或择优.它主要由两部分组成:
(1)获取决策信息.决策信息一般包括两个方面的内容:属性权重和属性值。
(2)通过一定的方式对决策信息进行集结并对方案进行排序和择优。信息集结方法有很多,本节只用加权算术平均(WAA)算子,就相当于计算加权平均数。
1. 加权算术平均算子(WAA)


2. 属性值归一化处理

- 效益型

- 成本型

- 固定型、偏离型

- 区间型、偏离区间型

二、适用问题
- 面临多种方案时,根据多个属性及一定的标准选择某一种方案:
- 例如:
- 银行根据多个属性对公司进行评估
三、算法总结
1. 步骤
- 建模构建决策矩阵
- 属性值归一化
- 对各个属性构造成对比较矩阵计算属性权重
- 计算每个公司的WAA
四、应用场景举例(企业评估)

1. 建模构建决策矩阵
划分各类属性指标的类型,并构建决策矩阵
2. 属性值归一化
根据属性指标类型,代入公式,进行归一化处理

3. 对各个属性构造成对比较矩阵计算属性权重(层次分析法)
可以参考层次分析法进行属性权重计算


4. 计算每个公司的WAA
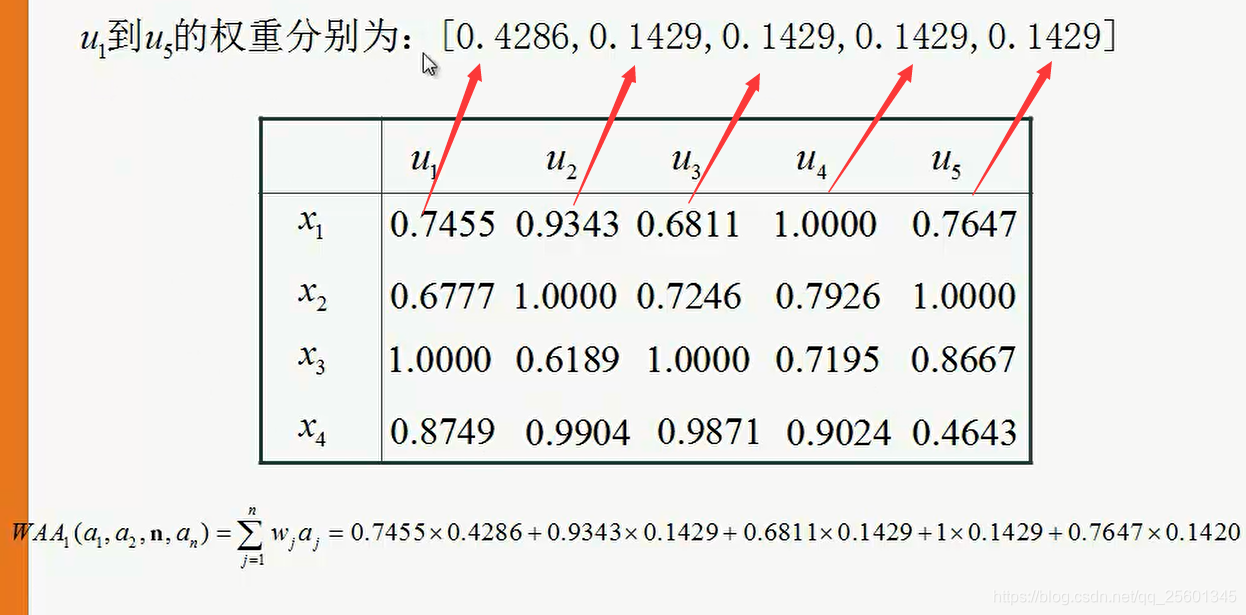

五、MATLAB代码
代码是层次分析法的
disp('请输入判断矩阵A(n阶)');
A=input('A=');
[n,n]=size(A);
x=ones(n,100);
y=ones(n,100);
m=zeros(1,100);
m(1)=max(x(:,1));
y(:,1)=x(:,1);
x(:,2)=A*y(:,1);
m(2)=max(x(:,2));
y(:,2)=x(:,2)/m(2);
p=0.0001;i=2;k=abs(m(2)-m(1));
while k>p
i=i+1;
x(:,i)=A*y(:,i-1);
m(i)=max(x(:,i));
y(:,i)=x(:,i)/m(i);
k=abs(m(i)-m(i-1));
end
a=sum(y(:,i));
w=y(:,i)/a;
t=m(i);
disp(w);
%以下是一致性检验
CI=(t-n)/(n-1);RI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];
CR=CI/RI(n);
if CR<0.10
disp('此矩阵的一致性可以接受!');
disp('CI=');disp(CI);
disp('CR=');disp(CR);
end
六、实际案例
[1 3 3 3 3;
1/3 1 1 1 1;
1/3 1 1 1 1;
1/3 1 1 1 1;
1/3 1 1 1 1;]

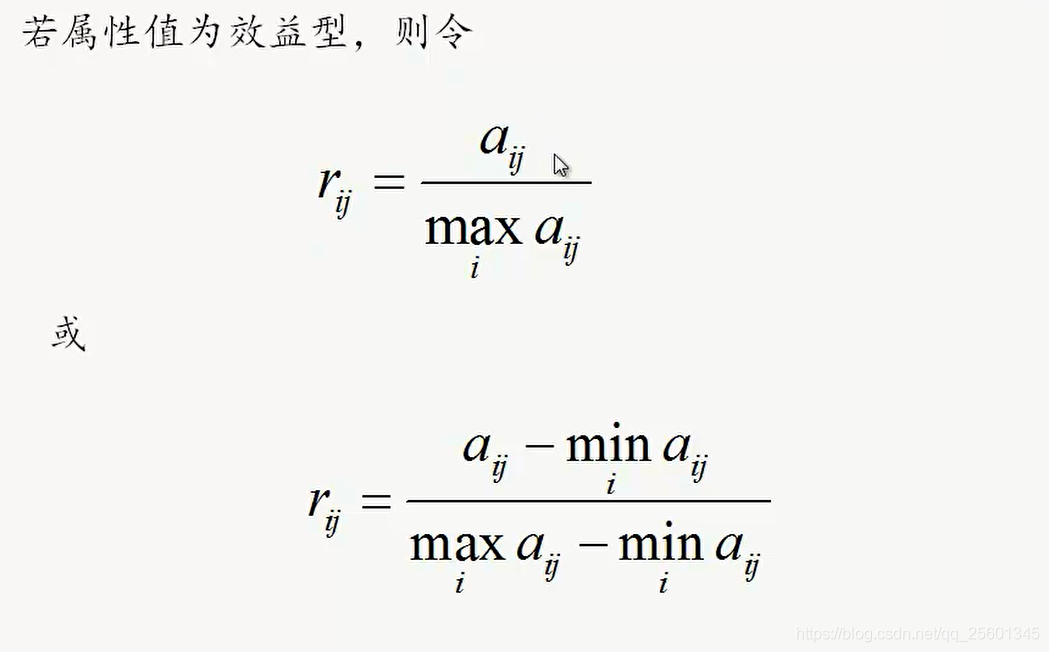



版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/bian-cheng-ji-chu/105837.html