1. 首页首页
  2. 编程基础编程基础

2025年已知三角形三边长怎么求面积_解三角形问题中的常见错解分析

编程基础 • • 阅读 29

已知三角形三边长怎么求面积_解三角形问题中的常见错解分析解三角形问题是个难点 怎样才能突破这个难点呢 只有正确理解三角形中的边角关系 即三角形中的边角等量关系 边角的不等关系及内角和关系 才能克服这个难点

f68ccc811a93f99c58b175ee1387c74c.png

解三角形问题是个难点，怎样才能突破这个难点呢？

只有正确理解三角形中的边角关系，即三角形中的边角等量关系、边角的不等关系及内角和关系，才能克服这个难点。

下面快和包sir一起对解三角形问题中的常见错误进行分析。

b554c2c0b5fd8ac933108106dd42eb9d.png

一、不注意三角形的边角关系，造成角的范围变化而致错

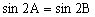
cfb1b66f6554d7fc3eb7ae46903ace4e.png

例1 在△ABC中，，试判断三角形的形状。

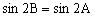
9bb25289cd1e986f730cf5981fa482f3.png

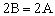
087433a751df8b8ec54789c66c9c0f37.png

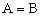
f399bdf427ec1232c3d9aaf390910e87.png

错解：由，得，所以，知此三角形为等腰三角形。

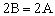
087433a751df8b8ec54789c66c9c0f37.png

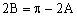
af20d1895109694a9931cfcc8eb0d748.png

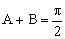
3846f9d214d572c35d8d6bb0b99881e1.png

分析：上面的式子不是等价变换，未考虑三角形中角的范围而致错。由已知得或，所以A=B或。

故△ABC是等腰三角形或直角三角形。

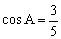
df984d5469fc1169f281d0a971ee10a7.png

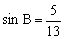
2c7b905fe2a4009b33115c84aa217f68.png

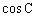
6805eca7f61fbd64a51826b39aa4c77c.png

例2 A、B、C为△ABC的内角，且，，求的值。

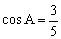
df984d5469fc1169f281d0a971ee10a7.png

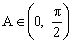
b809163fc44bdf9a84041abc4d70d583.png

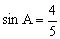
371af172c5d658c3aed3c7af651a5571.png

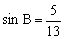
2c7b905fe2a4009b33115c84aa217f68.png

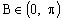
84dd9b710678c1d0e400586a24fa884c.png

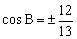
e42c65c0e2aea31cfd69382917175a72.png

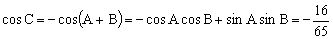
7ccdf8502869ae890b175497c10f1ca6.png

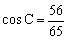
64dec5d67a45866addf52c04cc66e797.png

错解：由，知，得，，知，所以，从而或。

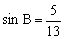
2c7b905fe2a4009b33115c84aa217f68.png

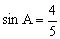
371af172c5d658c3aed3c7af651a5571.png

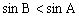
7c67b6dbd8822b4efcc8d35d5fabfd3d.png

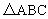
9616eae4b10a31d7b8fd6ab56e647d62.png

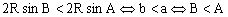
5ef1483bc4dbbe48dc4c768c239947da.png

分析1：由于，，故，两边乘以外接圆的直径2R，得。

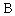
be9a386ff32d634ed177a0f42198fa36.png

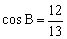
627b42f10b4ede13dbc054f2004a8b85.png

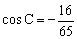
29d226af386b1572b75f078fb0b684e2.png

故角一定是锐角，于是，知。

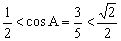
e388734fb41115d0c8167c93504e5ac7.png

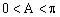
6128473da50b7b9d8e11fdea7b28c7d3.png

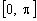
a71d0b896bd89932b2b9c8ef97d7d4b1.png

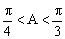
284fa73936d723d91e15aaec4052b6a3.png

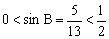
f5c0a0777e447647f8316b7e7f489881.png

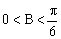
ad718cc9fb0afa1f65ee785c6d76af3a.png

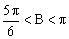
fa17a13c9f236e0574fd50509b64def2.png

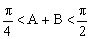
9c4b8b9274c847cc46c8c84586db1a8c.png

5a8cb0c048342bc3fce6a20a5dc46838.png

分析2：由且，而余弦函数在上为减函数，得，由，得或。所以或（不合题意），显然B为锐角。（以下过程请同学们自己做一做）

为了得到第三种解法，下面给出一个命题。

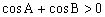
3eb67f1635be9efc81f62e6d0685d2fa.png

命题：在△ABC中，给定角A、B的正弦值或余弦值，则角C的正弦或余弦有解（即存在）的充要条件是。

证明：角C有解

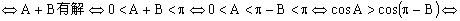
0ee66b6b899b5464cf05b8bade755236.png

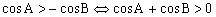
59fe6e72eb7ad6768d2a5c0cc684bdac.png

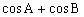
3aa11ce8bde47ff3e25114174b0d4bfa.png

故判断角C是否有解，只需考虑的符号。

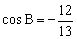
1d443aadd95a423d9bb272ae2bc289c9.png

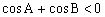
ecd5f701f2ceda118b310b15b0c79006.png

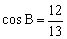
627b42f10b4ede13dbc054f2004a8b85.png

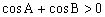
3eb67f1635be9efc81f62e6d0685d2fa.png

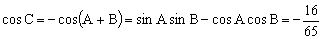
132955bc7835e4621428e77b00e518d3.png

分析3：利用上面的命题可轻易得解，当时，，此时角C无解；当时，，此时角C有解，故。

二、讨论问题不彻底而致错

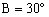
dd064de2a329f5e24698e71728cb3e2d.png

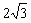
9316d1f095cf2481520d269c496f9fa3.png

例3 已知△ABC中，，AB=，AC=2，求△ABC的面积。

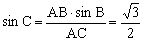
eca5da8636238d5d2850e8df19f753c3.png

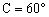
8e404218353db73190962b8ff0417184.png

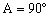
f84ea0064c9a3429de0185a0eeabcd43.png

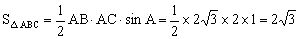
e584c26d9e98f3806ff9a8eb351df0c3.png

错解：由正弦定理得，所以，得，故。

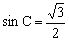
903b1ec40c14c43e3709f85e1c6b4f24.png

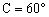
8e404218353db73190962b8ff0417184.png

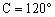
aaac96094aac8c0b5ba4cb4baf8a3056.png

分析：实际上，由可得或，因为它们都满足“大边对大角，小边对小角”的条件。

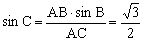
eca5da8636238d5d2850e8df19f753c3.png

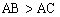
f249493a4a8a6d58ace1d69a90bb89f5.png

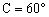
8e404218353db73190962b8ff0417184.png

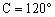
aaac96094aac8c0b5ba4cb4baf8a3056.png

由正弦定理得，又因，所以或。

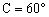
8e404218353db73190962b8ff0417184.png

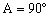
f84ea0064c9a3429de0185a0eeabcd43.png

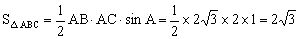
e584c26d9e98f3806ff9a8eb351df0c3.png

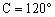
aaac96094aac8c0b5ba4cb4baf8a3056.png

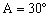
e6897853acbe5356e2e592ac28dfe8cf.png

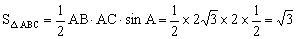
f22e9b8db7efbbb18dd90decb668f6c3.png

当时，，于是，当时，，于是。

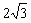
9316d1f095cf2481520d269c496f9fa3.png

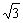
7505908d1c8cd80af4f0d52e97700d60.png

故△ABC的面积是或。

三、忽视取最值条件而致错

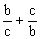
ae24df7b9ba28e9f63d628ec56bc530e.png

例4 在△ABC中，a、b、c分别是角A、B、C的对边，D是BC边上一点，AD⊥BC，垂足为D且AD=BC=a，求的最大值。

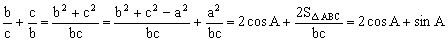
c1afbe4a531315c9e9556ee66645a422.png

错解：

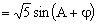
78d456a1876fdf93fa2161671c61c016.png

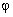
8ad0d107c7eb5d8c6b7c3111971d9a22.png

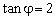
90645668b3022b3933d7aa7e01044169.png

（由所确定）。

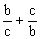
ae24df7b9ba28e9f63d628ec56bc530e.png

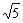
0a63b1ac861131299436e8c888735e5b.png

∴的最大值是。

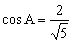
6baad6b1956dc36505ccc56f9972b42c.png

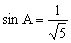
f9767ba421498c00027523cb02f66a78.png

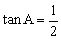
d46c4951dbc864f3fb12f11314fd61c8.png

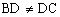
9fbbc978704661d2dfb72289397c7f2d.png

<br> (二维码自动识别)

283a9573ed068d99a20b4187ab18cc0f.png

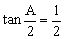
c76f6623e9ee6d23f277e55b37624e7a.png

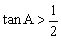
3a21b0f3aff7c9f0d6d14c1cdd3bf2de.png

分析：在上述错解中，*式等号成立的条件是当且仅当，，即，当时，∠CAD和∠BAD两者必有一个其正切值大于，而当时，，无论哪种情况必有，就是说*式中等号不能成立。

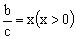
57dc81ba7ca1ef3059f5591645ba8833.png

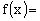
4c36d1bb1be27874c63c41ae5e558f6b.png

设，则，

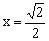
874d8af9df148698b584471de22d3b87.png

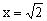
c8949a8689db8c577bb1b466abc6bb40.png

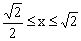
c7bb58fa53616376f1ec885af91264ff.png

当点D、C重合时，当点D、B重合时，故。

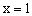
70528c296a56791fea92da0aa7c26b58.png

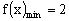
4486272b5d6a1d88d9ac148291f1ba1e.png

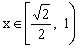
17a541b2a37ea6cdc79e7c3ef137a15c.png

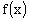
7a76ebb746a17a787a8325465591ed1c.png

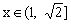
204bc77b5b318cc4b53f303ea98765db.png

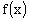
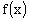
7a76ebb746a17a787a8325465591ed1c.png

7a76ebb746a17a787a8325465591ed1c.png

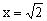
c8949a8689db8c577bb1b466abc6bb40.png

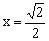
874d8af9df148698b584471de22d3b87.png

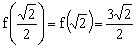
ef7d05226c03434b9dcbf2118eba6c0e.png

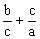
ecf8f7bc9718ceee1bd653d8d30d0abc.png

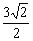
021c42d677ef477874e665ef34a3c0d1.png

显然时，，当时，由函数单调性定义知递减，当时，递增，所以的最大值在或时取得，因，所以的最大值是。

四、忽视构成三角形的条件而致错

8e2317d1818567ed0430378016c50df3.png

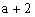
4c968f60f855b3066f2b0c378fb36e14.png

例5 a、、为钝角三角形的三边，求a的范围。

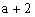
4c968f60f855b3066f2b0c378fb36e14.png

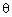
e7e5b0adff9cf12dd098ade25faf63ed.png

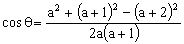
cbc1d9996dfaf88542a11aa18e61ae46.png

错解：为最大边，设它的对角为，由余弦定理知

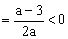
1d7c50de701efe9745ce67a9f5cbc648.png

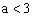
f677df19203a322f565918d22e2f21ac.png

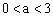
392021bb54aefa31a770157fe64e9c61.png

，得，所以。

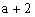
4c968f60f855b3066f2b0c378fb36e14.png

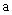
745b8445f52717081361860b339039bc.png

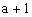
8e2317d1818567ed0430378016c50df3.png

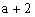
4c968f60f855b3066f2b0c378fb36e14.png

分析：此解法是不完整的，只考虑最大边的对角为钝角，没有注意、、三边能否构成三角形，因此还应该注意“三角形中的两边之和大于第三边”这个隐含条件。

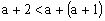
52a20c9cf0fde9b21ddad54ba45a0e4d.png

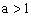
f44ec17f03c987e75c532b1d0502379f.png

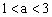
e478917712507179c1ca92affdb3f2a3.png

由上述解法并结合知，故a的范围是。

从上述各例中，我们可以看到忽视各种条件对角范围的制约，就可能导致错解。因此在三角形问题中，要认真审题，洞察和显化隐含条件，只有这样才能提高解题的正确率。

▍ 声明：文章综合整理自网络，版权归原作者所有，如有侵权，请联系删除，

编程小号
上一篇 2025-07-21 14:01
下一篇 2025-06-01 20:21

相关推荐

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容， 请发送邮件至 举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/bian-cheng-ji-chu/79151.html