目录
一、前言
图像矩,opencv学习笔记的最后一个内容了。写完这个,学习笔记也就写完了,后续如果有精力,还会再写一些代码实战的,感谢大家的支持。
如果想看其他有关于OpenCV学习方法介绍、学习教程、代码实战、常见报错及解决方案等相关内容,可以直接看我的OpenCV分类:
【opencv学习笔记】031 之 矩概念与图像矩详解
如果你想了解更多有关于计算机视觉、OpenCV、机器学习、深度学习等相关技术的内容,想与更多大佬一起沟通,那就扫描下方二维码加入我们吧!

二、矩概念详解
矩这个东西,能组成的名词太多了,矩形,就是长方形,矩阵,就是m行n列的二维数组,所以想了解矩,就要从其具体的场景中去理解。
今天我们要讲的图像矩,就是一个新的概念,图像矩就是图像的矩,这个概念来源于数学中的矩,所以我们要先来理解一下,数学中的矩。首先我们先来看一下它的定义和相关概念:
在数学和统计学中,矩(moment)是对变量分布和形态特点的一组度量。当所有的变量矩的定义是各点对某一固定点离差幂的平均值。n阶矩被定义为一变量的n次方与其概率密度函数(Probability Density Function, PDF)之积的积分。在文献中n阶矩通常用符号μn表示。
直接使用变量计算的矩被称为原始矩(raw moment),移除均值后计算的矩被称为中心矩(central moment)。
讲完了概念之后,我们从公式来直观的看一下矩到底长啥样。
1、离散情况
我们从矩的概念出发,我们先考虑离散情况:
假设有一个离散的随机变量X,用A表示一个常数,用k来表示幂(阶数)。那么我们有下面这个公式:
这个称为X关于点A的k阶矩。
如果这个常数A为0,我们把这个k阶矩称之为k阶原点矩。
如果这个常数A为X的均值E(X),我们把这个k阶矩称之为k阶中心矩。
变量的一阶矩是数学期望(expectation),表示分布重心;
变量的二阶矩是方差(variance),表示离散程度;
变量的三阶矩是偏度(skewness),表示分布偏离对称的程度;
变量的四阶矩是峰度(kurtosis),描述分布的尖峰程度,例如正态分布峰态系数=0。
如果我们有两个离散随机变量:X,Y。A1,A2分别代表对应于两个随机变量的常数,用p,q表示幂(阶数),那么我们有下面的公式:
这个称为X,Y关于点A1,A2的p+q阶矩。
如果两个常数都是0,那么我们称之为p+q阶混合原点矩。
如果两个常数都是对应的均值,即A1=E(X),A2=E(Y),那么我们称之为p+q阶混合中心矩。
2、连续情况
接下来我们考虑连续情况:
假设有一个连续的随机变量x,其单变量的概率密度函数为f(x),用A表示一个常数,用k来表示幂(阶数)。那么我们有下面这个公式:
这个称为X关于点A的k阶矩。
如果我们有两个连续的随机变量:x,y,两个变量的联合概率密度为f(x,y)。A1,A2分别代表对应于两个随机变量的常数,用p,q表示幂(阶数),那么我们有下面的公式:
这个称为x,y关于点A1,A2的p+q阶矩。
三、图像的几何矩
1、几何矩的概念
了解了矩的概念,我们接下来说一下图像的几何矩。在图像中,矩的概念如下:
矩是描述图像特征的算子。
这里的图像是单通道,也就是灰度图像,相当于一个矩阵,也就是上面提到的离散的情况。矩阵上每个位置的取值范围是0-255的整数。
2、图像的p+q阶矩
图像p+q阶矩的定义公式如下:
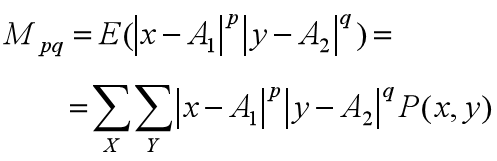
当p+q = 0时,为零阶矩:

当p+q = 1时,为一阶矩:

当p+q = 2时,为二阶矩:

通过上面的结果,我们也可以得到图像的重心坐标和图像的方向,这个时候的固定点为(0,0),所以:
图像的重心坐标为:

物体形状方向为:

3、HU矩
在图像矩中有HU矩,这是Hu在1962年提出的,主要有:
(1)原点矩
(2)中心矩
(3)归一化中心矩
1.原点矩
原点矩就是固定点的坐标为(0,0)。其公式如下:
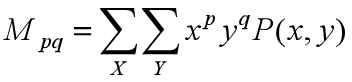
2.中心矩
中心矩就是以固定点(x0,y0)为中心:

3.归一化中心矩
归一化中心矩就是对中心矩做归一化处理:

4、相关API
1.Moments类
在讲API之前,我们先说一下Moments类,它的定义如下:
class CV_EXPORTS_W_MAP Moments { public: //! the default constructor Moments(); //! the full constructor Moments(double m00, double m10, double m01, double m20, double m11, double m02, double m30, double m21, double m12, double m03 ); //! @name spatial moments CV_PROP_RW double m00, m10, m01, m20, m11, m02, m30, m21, m12, m03; //! @name central moments CV_PROP_RW double mu20, mu11, mu02, mu30, mu21, mu12, mu03; //! @name central normalized moments CV_PROP_RW double nu20, nu11, nu02, nu30, nu21, nu12, nu03; };它有两个默认构造函数和三组double类型的数据,
第一组数据:spatial moments(空间矩)对应的是我们前面讲到的原点矩的零阶矩、一阶矩、二阶矩和三阶矩。
第二组数据:central moments(中心矩)对应的是我们前面讲到的中心矩的二阶矩和三阶矩。
第三组数据:central normalized moments(归一化中心矩)对应的是我们前面讲到的归一化中心矩的二阶矩和三阶矩。
2.moments函数
Moments moments( InputArray array, bool binaryImage = false );函数参数含义如下:
(1)InputArray类型的array,输入的光栅图像(单通道、8位或浮点二维数组)或二维点的数组。
(2)bool类型的binaryImage,如果为true,则所有非零图像像素都被视为1。该参数仅用于图像。
3.contourArea函数
double contourArea( InputArray contour, bool oriented = false );函数参数含义如下:
(1)InputArray类型的contour,二维点(轮廓顶点)的输入向量,存储在std::vector或Mat中。
(2)bool类型的oriented,面向区域标志。如果为真,则函数将根据轮廓方向(顺时针或逆时针)返回带符号区域值。使用此功能,可以通过获取区域的符号来确定轮廓的方向。默认情况下,参数为false,这意味着返回绝对值。
4.arcLength函数
double arcLength( InputArray curve, bool closed );函数参数含义如下:
(1)InputArray类型的curve,二维点的输入向量,存储在std::vector或Mat中。
(2)bool类型的closed,指示曲线是否闭合的标志。
5、代码展示
#include <opencv2/opencv.hpp> #include <iostream> using namespace std; using namespace cv; Mat src, gray_src; int threshold_value = 80; int threshold_max = 255; const char* input_win = "【输入图像】"; const char* output_win = "【输出图像】"; const char* trackbar_title = "Threshold:"; RNG rng(12345); void Demo_Moments(int, void*); int main() { src = imread("E:/image/moments.png"); if (!src.data) { cout << "could not load image !"; waitKey(0); return -1; } cvtColor(src, gray_src, CV_BGR2GRAY); GaussianBlur(gray_src, gray_src, Size(3, 3), 0, 0); namedWindow(input_win, CV_WINDOW_AUTOSIZE); namedWindow(output_win, CV_WINDOW_AUTOSIZE); imshow(input_win, src); createTrackbar("Threshold", output_win, &threshold_value, threshold_max, Demo_Moments); Demo_Moments(0, 0); waitKey(0); return 0; } void Demo_Moments(int, void*) { Mat canny_output; vector<vector<Point>> contours; vector<Vec4i> hierachy; Canny(gray_src, canny_output, threshold_value, threshold_value * 2, 3, false); findContours(canny_output, contours, hierachy, RETR_TREE, CHAIN_APPROX_SIMPLE, Point(0, 0)); vector<Moments> contours_moments(contours.size()); vector<Point2f> ccs(contours.size()); for (size_t i = 0; i < contours.size(); i++) { contours_moments[i] = moments(contours[i]); ccs[i] = Point(static_cast<float>(contours_moments[i].m10 / contours_moments[i].m00), static_cast<float>(contours_moments[i].m01 / contours_moments[i].m00)); } Mat drawImg;// = Mat::zeros(src.size(), CV_8UC3); src.copyTo(drawImg); for (size_t i = 0; i < contours.size(); i++) { if (contours[i].size() < 100) { continue; } Scalar color = Scalar(rng.uniform(0, 255), rng.uniform(0, 255), rng.uniform(0, 255)); printf("center point x : %.2f y : %.2f\n", ccs[i].x, ccs[i].y); printf("contours %d area : %.2f arc length : %.2f\n", i, contourArea(contours[i]), arcLength(contours[i], true)); drawContours(drawImg, contours, i, color, 1, 8, hierachy, 0, Point(0, 0)); circle(drawImg, ccs[i], 1, color, 1, 8); } imshow(output_win, drawImg); }
6、执行结果
center point x : 451.00 y : 295.00 contours 2 area : 6493.00 arc length : 307.08 center point x : 451.00 y : 295.00 contours 3 area : 6451.00 arc length : 304.74 center point x : 296.00 y : 296.00 contours 4 area : 7234.00 arc length : 318.39 center point x : 296.00 y : 296.00 contours 5 area : 7188.00 arc length : 316.05 center point x : 296.00 y : 296.00 contours 6 area : 5812.00 arc length : 285.42 center point x : 296.00 y : 296.00 contours 7 area : 5770.00 arc length : 283.08 center point x : 495.00 y : 196.00 contours 8 area : 7537.00 arc length : 326.39 center point x : 495.00 y : 196.00 contours 9 area : 7496.00 arc length : 324.05 center point x : 495.00 y : 196.00 contours 10 area : 6079.00 arc length : 293.42 center point x : 495.00 y : 196.00 contours 11 area : 6045.00 arc length : 291.08 center point x : 140.00 y : 158.00 contours 12 area : 9359.00 arc length : 367.36 center point x : 140.00 y : 158.00 contours 13 area : 9313.00 arc length : 365.02 center point x : 344.00 y : 128.00 contours 14 area : 5525.00 arc length : 306.45 center point x : 344.00 y : 127.00 contours 15 area : 5493.00 arc length : 304.11 center point x : 247.00 y : 90.00 contours 16 area : 6527.00 arc length : 317.28 center point x : 247.00 y : 90.00 contours 17 area : 6525.00 arc length : 314.94 center point x : 247.00 y : 90.00 contours 18 area : 5125.00 arc length : 281.97 center point x : 247.00 y : 90.00 contours 19 area : 5119.00 arc length : 279.62 

大家也可以自己尝试一下呀,一定要多做练习!
今天的文章 【opencv学习笔记】031 之 矩概念与图像矩详解分享到此就结束了,感谢您的阅读。



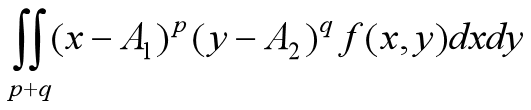
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/bian-cheng-ji-chu/84512.html