相机中的几个重要概念
在这里插入图片描述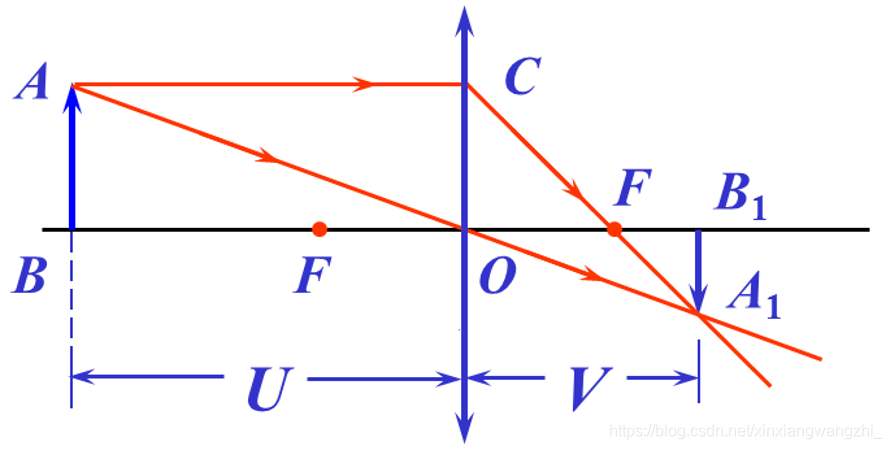
图3 物距,像距,焦距示意图
几个重要的概念:
1光心(O):optical center,可以把凸透镜的中心近似看作是光心。
2焦点:平行光经过凸透镜后汇聚成一个点,这个点称为焦点
焦平面:与成像系统的光轴垂直且包含成像系统焦点的平面。
像平面:与成像系统的光轴垂直且包含成像系统像点的平面。
像距V(主距):光心到像平面的距离
焦距F:光心到焦平面的距离
物距U:光心到物体的距离
根据图3有:
在这里插入图片描述
变焦(zoom):一个镜头一般由多个镜片组成,变焦就是改变焦距,最直观的反应是视场大小的变化。
对焦(调焦,focus):对焦和调焦是一回事,目的是使图像清晰,其原理是整体是镜头发生移动,焦距基本不变。 
景深:表示清晰范围。
弥散圆:可以表示对焦过程中,人眼能接受的清晰范围对应到影像上的尺度。
超焦距(很重要的一个概念,获取影像最基本的要清晰,总像获取的影像都是清晰的):目的是获取最大清晰的视场范围,如果我们使焦距等于超焦距,带入景深计算公式发现,后景深等于无穷,前景深为一个数,也就是说虽然超焦距能获取最大景深,但是对于前景深到镜头的这一段距离成像仍是不清晰的(实际测试中发现无穷远处并不是很清晰)。
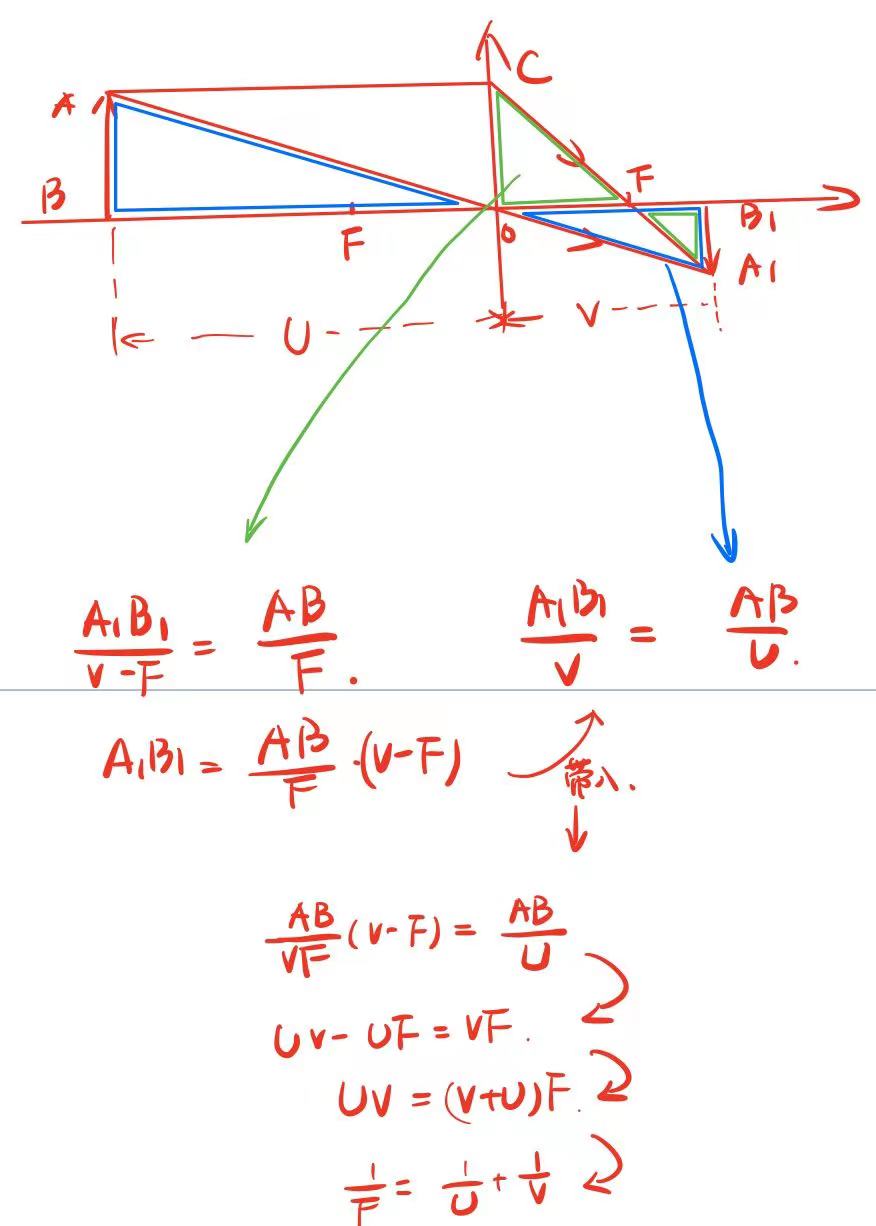
一、焦点与焦距的关系
在这里插入图片描述
二、俗称“调焦”并非调焦
焦距是透镜的参数,是指平行光经过透镜后形成的焦点到透镜中心的距离.
像距是物体经过透镜所成的像(成像平面)到透镜中心的距离,物体的远近不同,所成像离透镜中心的距离就不同.平时照相中所说的对焦是调整透镜的前后位置,使像落在底片上,这个时候的透镜焦距没有变化.
变焦镜头的焦距是可变的,可以调整广角的大小,焦距越小广角越大,看到的左右上下范围就越大
像平面处于焦点的后方
立体视觉(一 概述)_Zipcoder的博客-CSDN博客_立体视觉
立体视觉(一 概述)
现在给视差图一个通俗的理解:
视差图中每一个像素点的值是空间中相机光心到某一3D点的距离成比例所赋予的值(这句话写的有点绕,回头我再调整一下语序)。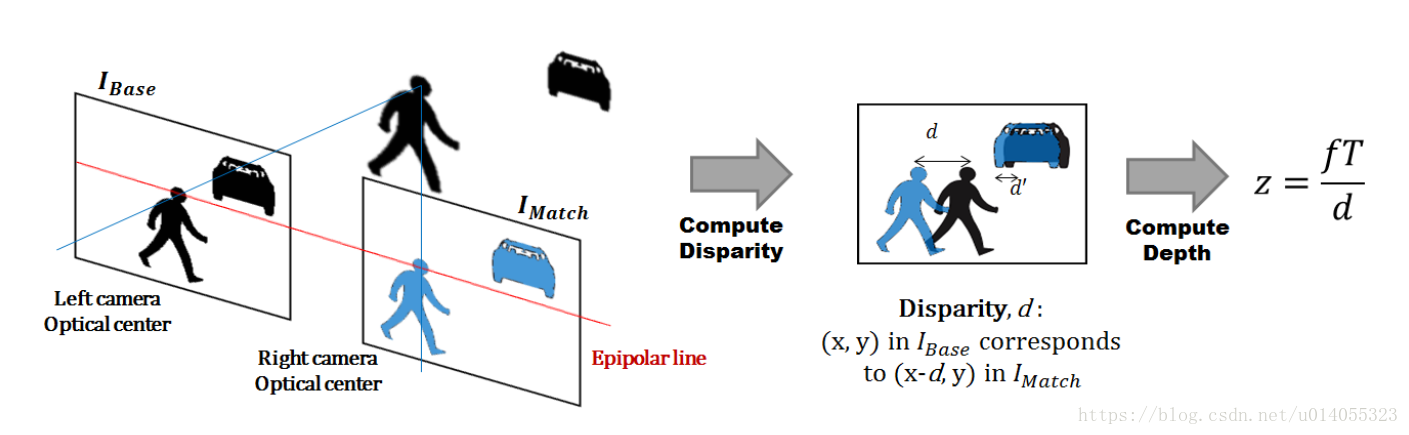
https://zhuanlan.zhihu.com/p/
白学立体视觉(2): 相机内外参数与坐标系
一、小孔成像
二、坐标系介绍
三、坐标系相互转换
1.世界坐标系到相机坐标系
由于世界坐标系和相机坐标系都是三维坐标系,所以他们之间的变换为刚体变换,即可以通过旋转和平移得到。坐标系之间的转换如下图所示: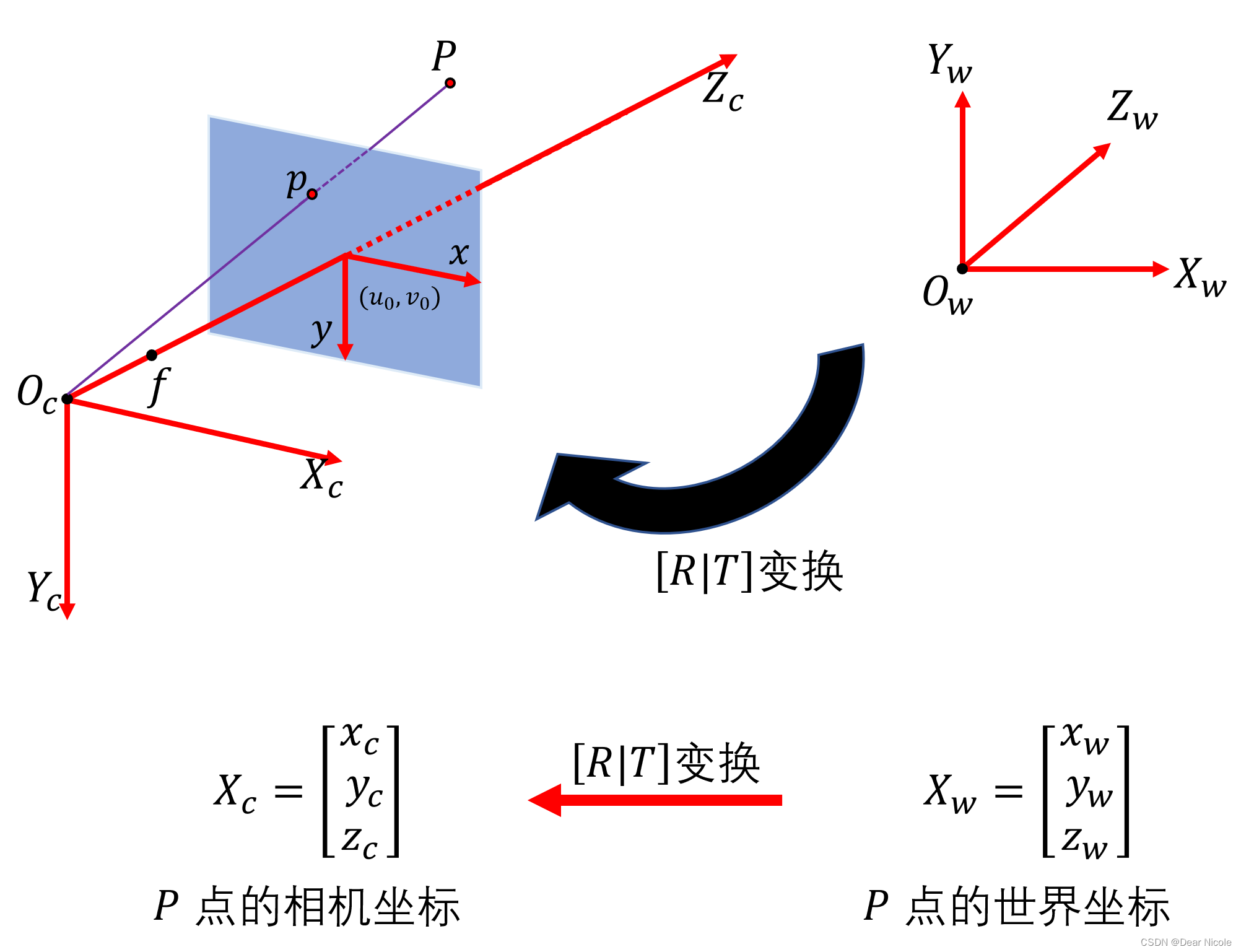
世界坐标系到相机坐标系的变换公式为:
相反,相机坐标系到世界坐标系的变换公式为:
相机中心在世界坐标系中的位置为(这个很重要):
2.相机坐标系到图像物理坐标系
如下图所示,相机坐标系下的点P通过透视投影,在图像物理坐标系上成像为p(x,y)。
根据相似三角形原理可以得到: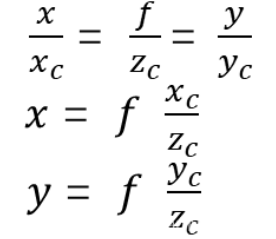
上式可以表示为矩阵形式,其中f为相机焦距,r是x轴和y轴的不垂直因子,也称物理坐标的扭曲因子,在现在的相机中一般r为0,通常在相机标定中忽略不计: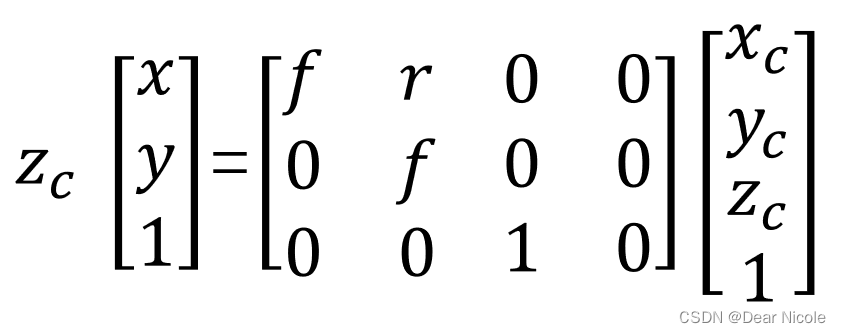
归一化像平面为一个虚拟的平面,与CCD成像平面平行,且距离相机光心距离为1。相机坐标系到归一化像平面坐标系之间变换如下图所示:
下图可以更可观的描述相机坐标系和归一化像平面坐标系之间的变换关系: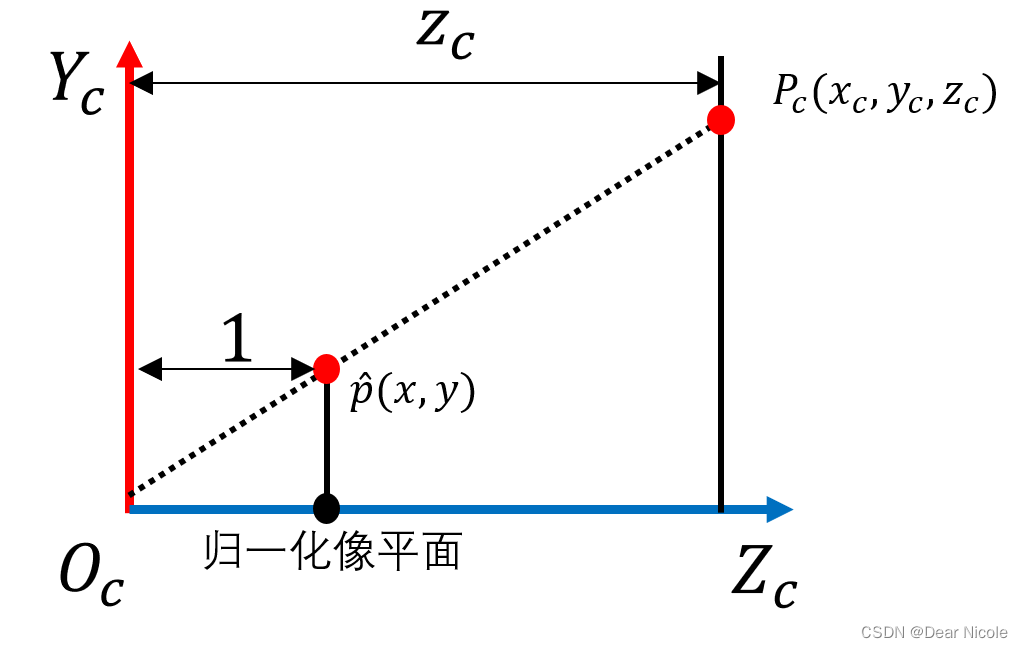
变换公式为: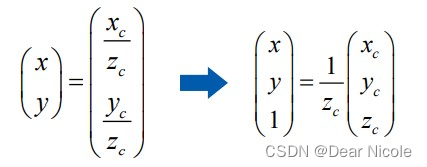
3.图像物理坐标系到图像像素坐标系

若O2在u,v坐标系中的坐标为(u0,v0,每一个像素在x轴与y轴方向上的物理尺寸为dx,dy,则图像中任意一个像素在两个坐标系下的坐标有如下关系: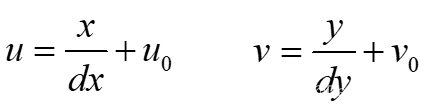
上式可以表示为矩阵形式: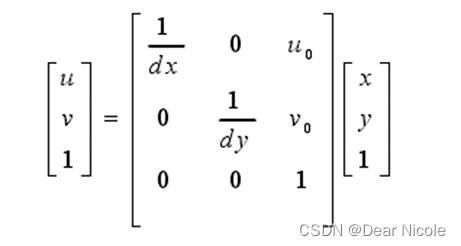
4.世界坐标系到图像像素坐标系
掌握了以上各个坐标系的转换关系,也就理解了相机透视投影的概念。下面我们可以把几个坐标系穿起来,得到世界坐标系表示的Pw点坐标与其投影点p的坐标(u,v)的对应关系: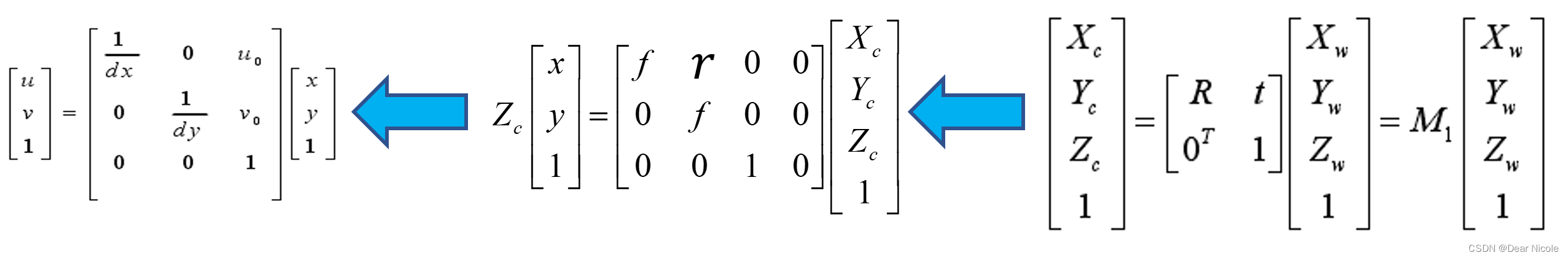
最终可以用下式表示: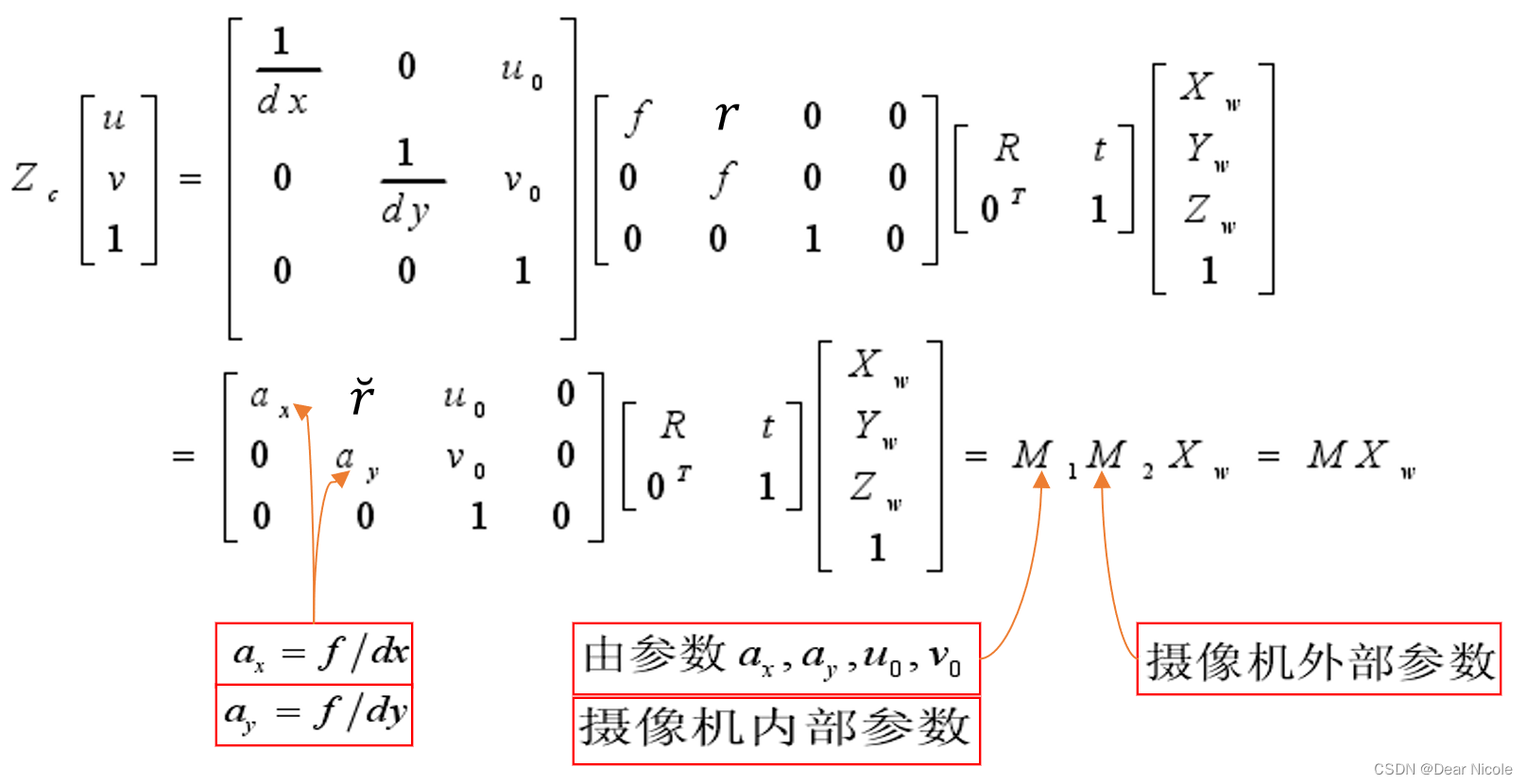
其中,ax、ay(ax 和 ay 被称为等效焦距,有时候也用Fx 和 Fy表示)、r、u0、v0为相机内参,R和t为相机外参。相机的内参和外参就是相机标定要计算的结果,相机标定将在后面小结进行详细的介绍。
三、镜头畸变
上述的相机模型为理想条件下的相机成像模型,而实际的成像过程往往存在偏差,即畸变。由于相机物镜系统设计、制作、装配等因素所引起的,像点偏离其理想位置点的误差称为光学畸变,如下图所示: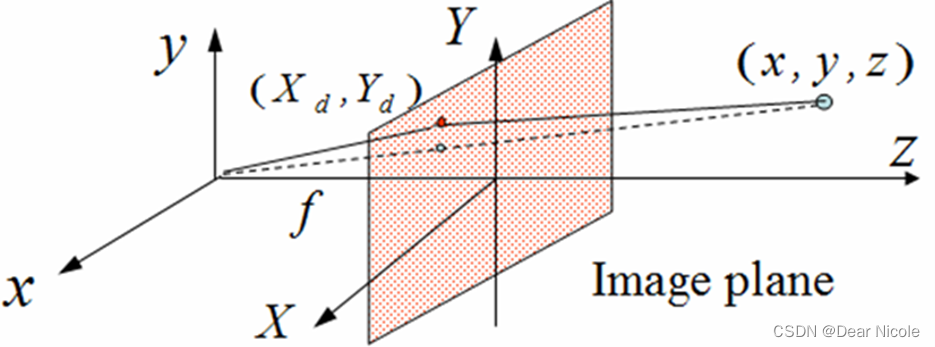
相机的针孔模型,只是真实相机的一个近似,由于存在各种镜头的畸变和变形,所以真实的相机要比模型复杂的多。在引入各种非线性的畸变修正之后,就形成看复杂的非线性成像模型。镜头的畸变主要分为径向畸变、离心畸变和薄棱镜畸变三类。
1. 径向畸变
定义:径向畸变像点沿径向方向偏离标准理想位置。径向畸变又分正向畸变和负向畸变,正向畸变称为枕形畸变,负向畸变称为桶形畸变;
特点:由镜头的形状缺陷所造成的畸变,关于相机主光轴对称。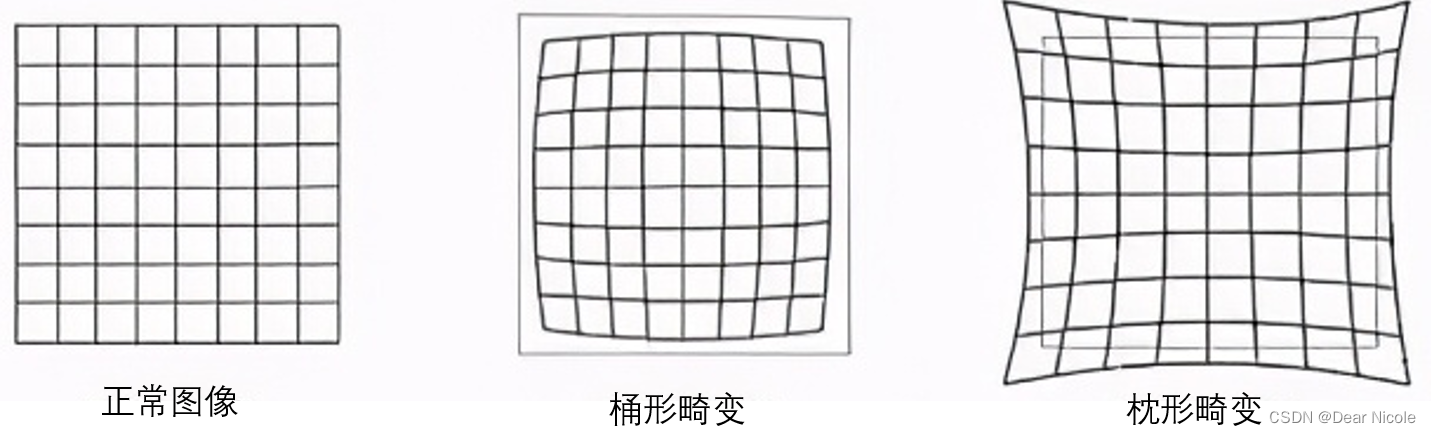 光学镜头径向曲率的变化是引起径向畸变的主要原因,这种变形会使得图像点沿径向移动,离中心点越远其变形的位移量越大。
光学镜头径向曲率的变化是引起径向畸变的主要原因,这种变形会使得图像点沿径向移动,离中心点越远其变形的位移量越大。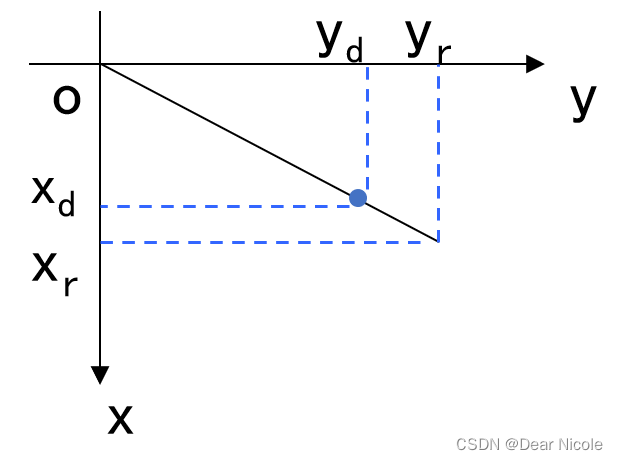
对于图像的径向畸变,通常采用多项式拟合算法,假设图像中的像素点理想的坐标为(Xd,Yd),畸变后坐标为(Xr,Yr),则: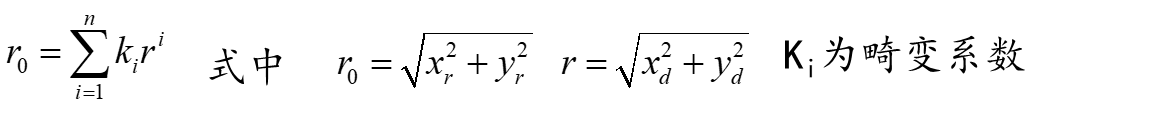 由于径向畸变只跟像素点离图像中心的距离有关,因此在直角坐标系中有:
由于径向畸变只跟像素点离图像中心的距离有关,因此在直角坐标系中有: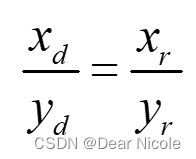
将该式带入上式得:
2. 离心畸变
定义:光学系统的光学中心和几何中心不一致(镜头各器件的光学中心)所造成的畸变;
特点:既包含径向畸变,又包含镜头主光轴不对称多造成的切向畸变。
由于镜头装配误差,组成光学系统的多个光学镜头的光轴不可能完全共线,从而引起离心畸变,这种畸变是由径向变形分量和切向变形分量共同构成,其数学模型为:
.3. 薄棱镜畸变
定义:镜头设计缺陷与加工安装误差所造成;
特点:同时引起径向畸变和切向畸变,高价位镜头可以忽略薄棱镜畸变。
薄棱镜畸变是指由光学镜头制造误差和成像敏感阵列制造误差引起的图像变形,这种变形是由径向变形分量和切向变形分量共同构成,其数学模型为:
白学立体视觉(3): 单目相机标定
一、为什么需要相机标定?
我们如果想重建出一台相机的成像过程的数学模型,相机的参数是最基本的。相机参数又分为内参和外参。那么内参和外参就是我们标定的最终目的。
1、有了内参中的畸变系数:[k1,k2,k3, …,p1,p2,…],我们就可以对带畸变的图像进行矫正,避免采集到的图像产生桶形畸变和枕形畸变。
2、有了相机内外参数,我们就可以构建相机成像的几何模型,从而把世界坐标系中的三维物体投影到二维平面上。
3、计算多台相机中间的映射关系,本节不详细介绍,后边有的是机会。(这个很重要,这将是双目视觉乃至多目立体视觉基础)。
相机内参:相机的内参(dx,dy,r,u0,v0,f);
一个像素在水平和垂直方向上的物理尺寸为dx和dy,单位为毫米(或者米);
焦距f,单位为毫米(或者米);
图像物理坐标的扭曲因子r,通常为0,忽略不计;
u0,v0为主点在图像像素坐标系下的坐标,单位为像素;主点为过光心垂直于成像面的垂线,该垂线与成像面的交点。
相机外参:[R|T];
世界坐标系转换到相机坐标系的旋转R和平移T矩阵。
畸变系数:[k1,k2,k3, …,p1,p2,…]。
我们只关心相机的径向畸变系数k1,k2,k3…,和相机的切向畸变系数p1,p2,~。
二、张正友标定法
1.标定板
张正友标定法应用比较广泛,操作也比较简单易实现。只需要一个角点特征明显,且易于提取的平面板。如下图所示:
标定板有以下几个制作要求:
1、标定板是一个二维平面。
2、标定板不反光,不透视,不易变形。
3、角点之间的物理距离是固定的,根据需要可以设为7cm,11cm等。
2.公式命名
本节公式主要来源于张正友论文,感兴趣的可以阅读一下原论文。
2D图像点坐标及其齐次坐标: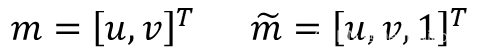
3D空间点坐标及其齐次坐标: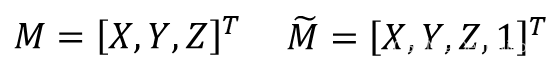
3D空间点到图像像素坐标的映射关系用下式表示:
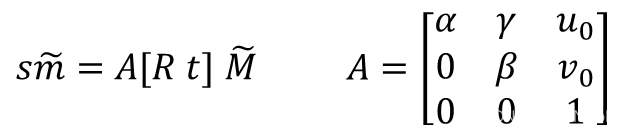
s:表示3D空间坐标系到图像坐标系的尺度因子
A:相机内参矩阵
(u0,v0):像主点坐标,
α , β:分别为图像u轴和v轴方向的焦距值(像素单位),也就是上小结中提到的ax、ay(ax 和 ay 被称为等效焦距,有时候也用Fx 和 Fy表示)
γ:为像轴的倾斜因子
三、OpenCV实践张氏标定法
1.标定步骤
1、准备一个标定板,按照上文提出的要求制作。为了简便也可以用A4纸打印,粘贴在一个平板上。
2、采集棋盘格标定板若干张图片,一般10至20张就够。但是每次拍摄,标定板角度和位置要改变。
3、检测图片中角点。
4、利用解析解估算方法计算出5个内部参数,以及6个外部参数
5、使用畸变公式的线性方程组求解近似的畸变系数(或者直接使用0也可以)
6、使用非线性优化法计算精确的内外参数和畸变系数。
2.标定实践

(SLAM)对单应矩阵的理解
假如我们去超市用支付宝付款,而扫描二维码的时候,我们不需要正对着二维码,而是多少带着点角度,你会发现就算偏转很大的角度也能识别出来。这其中的过程就是先将二维码从背景中提取出来,并且变成非常工整的矩形二维码。这个二维码是一个平面,所以满足同一个平面的要求。这就是单应矩阵的一个非常重要的应用:图像矫正。
除此之外单应矩阵还有很多的应用,例如:张正友相机标定法、图像拼接等。
两个相机在拍摄同一个平面的时候,就是如图所示的效果。
相机成像原理公式:
我们把简化一下其形式: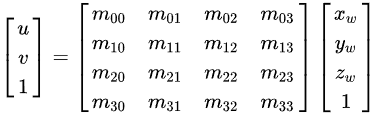
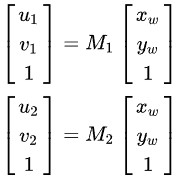
_M_矩阵是一个是一个44的矩阵,空间点在同一个平面上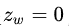 ,则_M_矩阵就变成了33的矩阵。相机不同位置所拍摄图像,得到的关系式为:
,则_M_矩阵就变成了33的矩阵。相机不同位置所拍摄图像,得到的关系式为:
整理合并就可以得到:
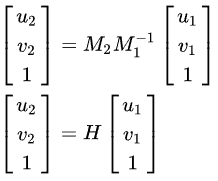
其中_H_就是单应矩阵。

版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/bian-cheng-ji-chu/87131.html