三角形费马点及深入拓展

一、费马点的定义

三角形内部满足到三个顶点距离之和最小的点，称为费马点。

二、费马点的证明

比较麻烦的一件事情是，当我们考虑一个三角形的费马点时，我们需要将三角形分为两类: ①三个内角均小于120°的三角形 ②有一个内角大等于120°的三角形。

这是为什么呢？现在我从第①类三角形来解释，原因就十分清楚了。

1.三个内角均小于120°的三角形

该证法的巧妙之处在于作出了定点A'

可以得出，此时费马点的位置P使得∠APB＝∠APC＝∠BPC＝120°，这也告诉了我们，为什么三角形三个内角要小于120°，否则三角形内不存在该点P。

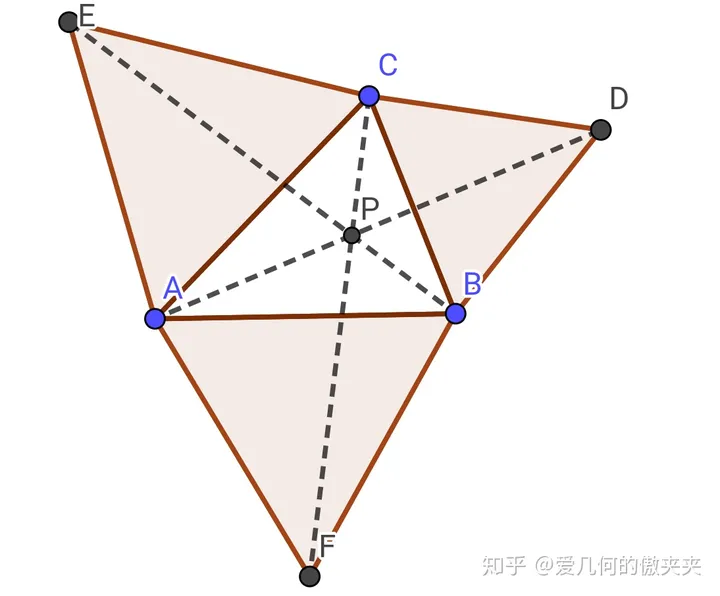
如上图，容易发现，以AB、BC、 AC为边向外作等边三角形，对应点连线三线交于一点P即为费马点。

实际上，我们称该P点为三角形ABC的第一费马点。

当等边三角形是向内作的时候，对应点的连线也会交于一点，我们称此时交点P为三角形ABC的第二费马点。

由于第一第二费马点的证明较为简单，本文不作赘述。

——————————分割线——————————

附: 费马点的另外一种证法

————————图源:几何瑰宝————————

2.三角形内有一角(∠BAC)大等于120°

①若∠BAC＝120°

此时费马点即为A点.

②若∠BAC＞120°

可知，费马点也在A点.

✔ 综上，当三角形内有一角(∠A)大等于120°时，点A即为费马点。

————————————————————————

总结:① 当三角形ABC内角均小于120°时，费马点P在三角形内部，满足∠APB＝∠BPC＝∠APC＝120°。

②当三角形ABC有一角大等于120°，费马点P即为最大角的顶点。

————————————————————————

那么既然我们知道了费马点P的位置，我们该如何计算此时的PA＋PB＋PC呢？

三、费马极值的计算

①当一个内角(∠A大等于120°)

此时费马极值即为AB＋AC＝b＋c.

比较简单，重点是三个内角都小于120°的情况。

②当三个内角均小于120°

即: 对于费马点P.(PA＋PB＋PC)²＝(a²＋b²＋c²)/2＋2根3×S

我个人也习惯称xyz的等式为费马等式.

四、广义费马点之一(直线型)(加权牛吃草)

这本质上就是光的折射

我们还能尺规作图作出该点:

如果题目给了确定的数据，我们可以利用正弦比算出正切之比，然后用相似进行尺规作图找出该点。

五、接下来就是重头戏了——加权费马点

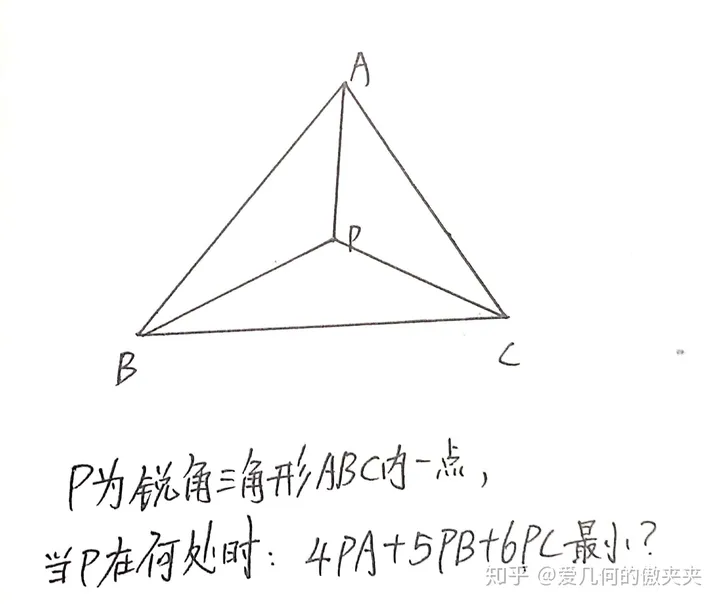
也就是说我们要尝试解决上面这个问题，当然，这题的难度还是很大的。

在讲解这道题之前，我们必须要有一个知识储备——著名的古堡朝圣问题.

①古堡朝圣问题

传说：从前有一个虔诚的信徒，他是集市上的一个小贩．每天他都从家所在的A点出发，到集市B点做买卖．到集市之前他要先拐弯儿到圆形古堡朝拜阿波罗神像．圆形古堡是座圣城，阿波罗像供奉在古堡的圆心O点上，而圆周上的点都是供信徒朝拜的顶礼点．这个信徒在想：我应该选择什么样的顶礼点，才能从家到顶礼点，然后再到集市的路程最短呢？(即下图问题)

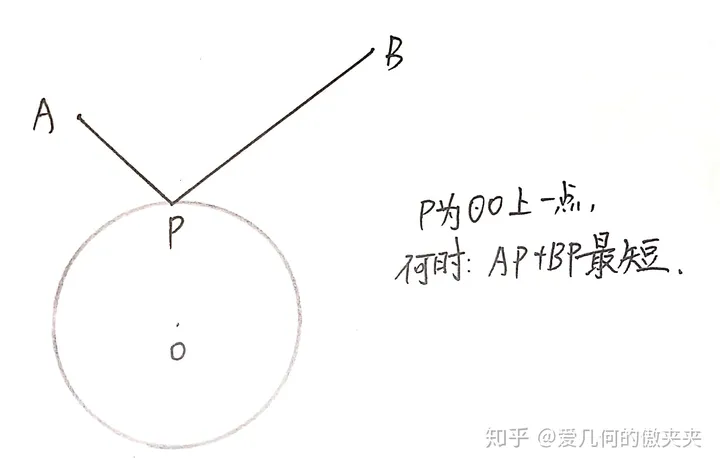
对于该问题，我们的思路是找出定量，设变量，求导计算。

我们发现一个很美丽的结论，当∠α＝∠β时，有最小值。但是很可惜的是，除非AB与圆有特殊位置关系，在其余时候我们是无法尺规作图得到该点P,这也算该题的一个遗憾之处。

② 加权古堡朝圣问题

我们进行更深入的思考，如果这个人是以v1的速度去拜佛，再以v2的速度去集市，那么该点P又要满足什么性质呢？

不难发现，只需要将上面的线段之和分别除以相对应的速度即可，过程也是大同小异。

最后的结论居然和直线型费马点结论一样!这也体现了几何的美妙之处。

③ 权重费马点(锐角三角形)

这是一个让无数数学爱好者望而生畏的题目。

这道题，初看让人觉得无从入手，主要原因是变量太多，所以我们采用减少变量的思维，先将BP长度固定，那么P就是在以B为圆心的圆上，然后去考虑其余的最值，发现此时本质上已经转化为了上文的加权古堡朝圣问题。

那么同理，固定CP时，我们能得到另外两角的正弦之比＝5/4，所以，我们最终想要的P点应该满足下图性质:

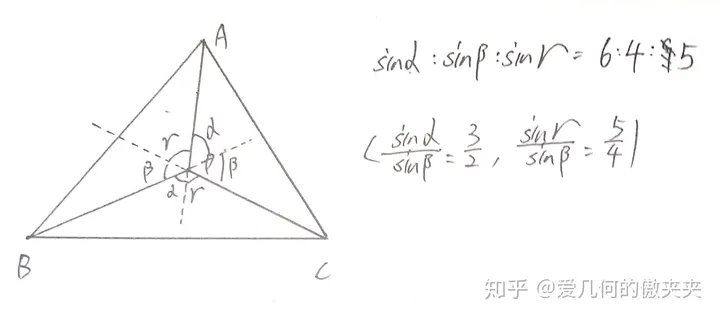
那么我们应该如何尺规作图确定该点呢？

很显然，α＋β＋γ＝180°.

那么由正弦定理，这三个角构成一个边长比为4:5:6的三角形.我们可以先尺规在平面上作出这个三角形MNL,那么它的三个内角就对应了αβγ.

由于α+β=180°－γ.其余同理.

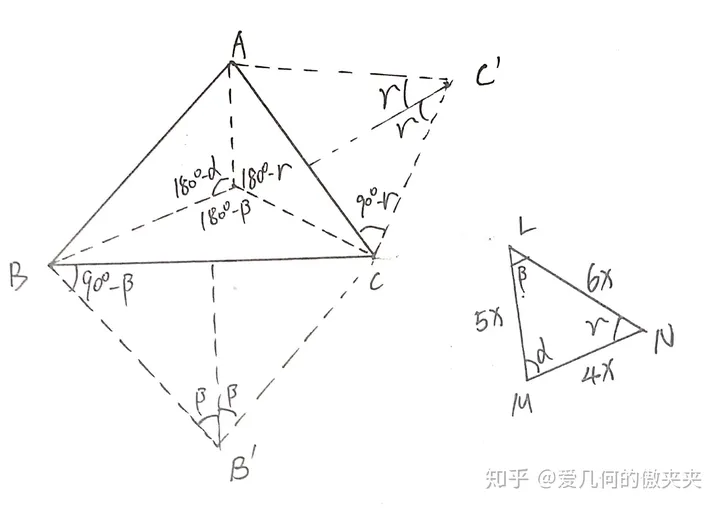
我们可以作BC中垂线，作∠B'BC＝90°－β.那么以B'为圆心B'B为半径的圆弦BC在上方所对角就是180°－β.同理，作出圆C'.两圆交点就是我们想要的权重费马点P了.

这类题看似得到了完美的解决，但是，上面之所以可以作出点P.主要利用了456可以构成三角形MNL.那么如果权重无法构成三角形呢？我们又该如何找出权重费马点?留给读者自己思考。

完~

手打不易，若文章对你有所帮助的话，可以点赞分享出去哦。

今天的文章三角形费马点及深入拓展分享到此就结束了，感谢您的阅读。

三角形费马点及深入拓展

三角形费马点及深入拓展

相关推荐