在自平衡中角动量守恒的原理分析

角动量守恒原理：

对于单个转动物质：角动量L=I*w（I:转动惯量,w：转动角速度）

一般形状的物体转动惯量计算如下：

1、对于细杆

（1）当回转轴过杆的中点(质心)并垂直于杆时，其中m是杆的质量，L是杆的长度，则转动惯量计算公式如下：

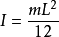
（2）当回转轴过杆的端点并垂直于杆时，其中m是杆的质量，L是杆的长度，则转动惯量计算公式如下：

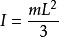
2、对于圆柱体

当回转轴是圆柱体轴线时，其中m是圆柱体的质量，r是圆柱体的半径，则转动惯量计算公式如下：

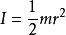
3、对于细圆环

当回转轴通过环心且与环面垂直时，则转动惯量计算公式如下：

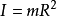
当回转轴通过环边缘且与环面垂直时，则转动惯量计算公式如下：

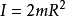
沿环的某一直径，R为其半径，则转动惯量计算公式如下：

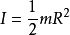
4、对于薄圆盘

当回转轴通过中心与盘面垂直时，则转动惯量计算公式如下：

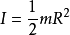
当回转轴通过边缘与盘面垂直时，R为其半径，则转动惯量计算公式如下：

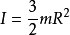
5、对于空心圆柱

当回转轴为对称轴时，R1和R2分别为其内外半径，则转动惯量计算公式如下：

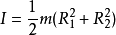
6、对于球壳

当回转轴为中心轴时，R为球壳半径，则转动惯量计算公式如下：

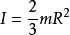
当回转轴为球壳的切线时，则转动惯量计算公式如下：

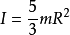
7、对于实心球体

当回转轴为球体的中心轴时，R为球体半径，则转动惯量计算公式如下：

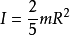
当回转轴为球体的切线时，则转动惯量计算公式如下：

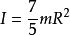
8、对于立方体

当回转轴为其中心轴时，L为立方体边长，则转动惯量计算公式如下：

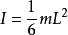
当回转轴为其棱边时，则转动惯量计算公式如下：

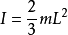
当回转轴为其体对角线时，则转动惯量计算公式如下：：

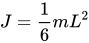
9、对于长方体，则转动惯量计算公式如下：

当回转轴为其中心轴时，式中l1和l2是与转轴垂直的长方形的两条边长：

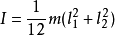
转动惯量的相对转动轴平移计算公式如下

I1=I0+m*S^2 其中I0是物体平移前转动惯量，S是转动轴平移距离，I1是物体平移后转动惯量

对于一个系统，里面包含有多个单一物体，则系统的角动量为：

$Ls=\sum In*\omega n$ 是系统内物体n的转动惯量， $\omega n$ 是物体n的转动速度。

我们知道对一固定点o,质点所受的合外力矩为零,则此质点的角动量矢量保持不变。这一结论叫做质点角动量守恒定律。因此对于一个合外力矩为零的系统，系统内的角动量守恒，即Ls保持不变。

如果此时系统内物体n的角动量发生变化，必有系统内其他物体合成一个与物体n相反的角动量，已维持角动量守恒。

两个转动体组成的系统角动量守恒分析：

结构如下图：蓝色圆柱体1和黄色圆柱体2，中间灰色的联动杆。

其中蓝色圆柱体内有一电机，中间灰色部分为电机输出轴，输出轴和黄色圆柱体固定。

分析这个整体系统的角动量：

t=0时，电机转速为0，蓝色L1和黄色L2的角动量都为零

t=1时，电机转速不为0，角速度为w2，此时黄色圆柱体L2=I2*W2;因为角动量守恒因此有L1=-L2=I1*W1。即w1=I2*W2/I1

因此可以通过电机控制黄色圆柱体的转动速度，来反作用控制蓝色圆柱体的转动速度和方向。

自平衡结构与控制：

简易自平衡结构如下：蓝色手柄状立在桌面，黄色圆柱体连接电机安装在蓝色手柄上。

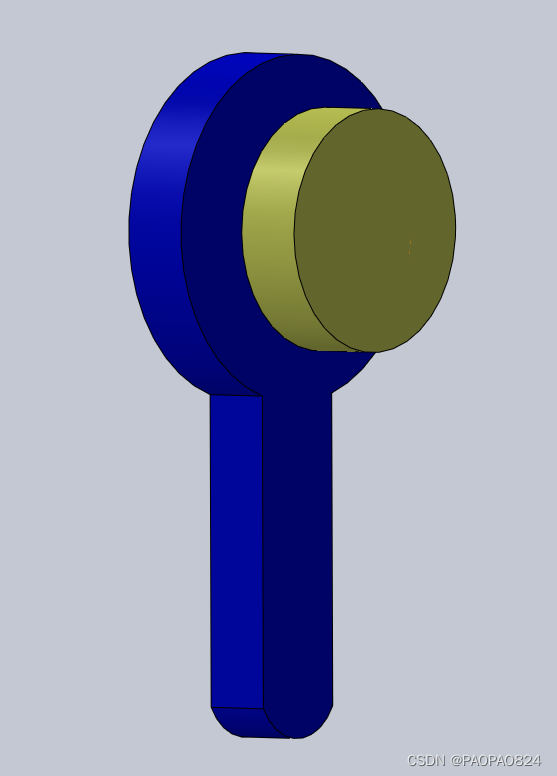
如上图

（1）到达平衡点时，蓝色圆柱体垂直立在桌面，黄色圆柱体为顺时针角速度w2（即电机转速）

（2）蓝色圆柱体发生扰动时

2.1蓝色圆柱体向左边扰动倾斜，此时蓝色圆柱体需要一个顺时针的转动（相对电机中心点）来抵消这个扰动。因为黄色蓝色物体组成系统在一个轻扰动作用下是角动量守恒，通过上面的两个转动体组成的系统角动量守恒分析可以知道自平衡的原理，让蓝色圆柱体产生一个顺时针的转动，需要黄色物体逆时针转动或者顺时针的转动速度减小。

2.2蓝色圆柱体向右边扰动倾斜，分析如同2.1

控制代码与算法：

由上面角动量守恒式子知道，需要知道系统内黄色和蓝色物体的转动惯量以及角速度，通过计算角速度的变化，计算出需要补偿的反向角速度变化。

结合输入变化和闭环反馈计算，可以使用PID算法，快速响应输出。

PID计算出电机的转速（实际是用PWM控制）

float PWM_Control(float Angle,float Gyro) {      float Bias;      int PWM;      Bias=Angle-Middle;  //===求出平衡的角度中值 和机械等重心分布相关      PWM=Balance_KP*Bias+Gyro*Balance_KD;   //===计算平衡控制的电机PWM  PD控制   kp是P系数 kd是D系数       return PWM; }

下面是定时中断中执行，更新扰动位置，更新PID输入与输出（控制电动转速）

 Encoder=Read_Encoder(3); //===Balance为了保证M法测速的时间基准，首先读取编码器数据 Encoder_Walk=Read_Encoder(2); Read_DMP(); //===更新姿态 Adjust=Get_Adc(Adjust_Ch); Middle=(Adjust-POTENTIOMETER)/392+3-Encoder/35; //+Motor_Turn Get_RC(Flag_Direction); Motor_Walk=Walk_Control(Encoder_Walk,Target_Walk), //直立 Motor_PWM=Balance_Control(Pitch,gyro[1])+Position_Control(Encoder); //动量 // Xianfu_Pwm(7000,110); //===PWM限幅 if(Turn_Off(Pitch,Voltage)==0) Set_Pwm(-Motor_PWM,Motor_Walk,Motor_Turn); //===赋值给PWM寄存器

今天的文章在自平衡中角动量守恒的原理分析分享到此就结束了，感谢您的阅读。

在自平衡中角动量守恒的原理分析

角动量守恒原理：

两个转动体组成的系统角动量守恒分析：

自平衡结构与控制：

控制代码与算法：

相关推荐