目录
一、函数
0x00 函数的定义
📚 数学中,f(x) = 2*x+1、f(x, y) = x + y 是函数...
在计算机中,函数是一个大型程序中的某部分代码,由一个或多个语句块组成;
它负责完成某项特定任务,并且相较于其他代码,具备相对的独立性;
📌注意事项:
1. 函数设计应追求“高内聚低耦合”;
(即:函数体内部实现修改了,尽量不要对外部产生影响,否则:代码不方便维护)
2. 设计函数时,尽量做到谁申请的资源就由谁来释放;
3. 关于return,一个函数只能返回一个结果;
4. 不同的函数术语不同的作用域,所以不同的函数中定义相同的名字并不会造成冲突;
5. 函数可以嵌套调用,但是不能嵌套定义,函数里不可以定义函数;
7. 函数的定义可以放在任意位置,但是函数的声明必须放在函数的使用之前;
📜 箴言:
1. 函数参数不宜过多,参数越少越好;
2. 少用全局变量,全局变量每个方法都可以访问,很难保证数据的正确性和安全性;
0x01 主函数
( 这里不予以赘述,详见第一章)
📌 注意事项
1. C语言规定,在一个源程序中,main函数的位置可任意;
2. 如果在主函数之前调用了那些函数,必须在main函数前对其所调用函数进行声明,或包含其被调用函数的头文件;
0x02 库函数
❓ 为什么会有库函数?
📚 “库函数虽然不是业务性的代码,但在开发过程中每个程序员都可能用得到,为了支持可移植性和提高程序的效率,所以C语言基础库中提供了库函数,方便程序员进行软件开发”
📌 注意事项:库函数的使用必须要包含对应的头文件;
📜 箴言:要培养一个查找学习的好习惯;
💡 学习库函数
1. MSDN;
2. c++:www.cplusplus.com;
3. 菜鸟教程:C 语言教程 | 菜鸟教程;
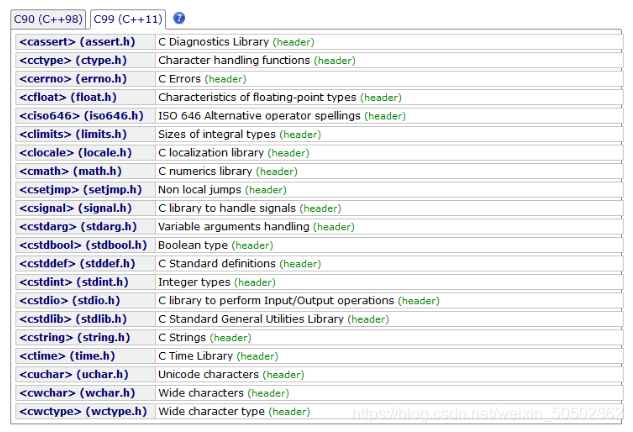
🔺 简单的总结:
IO函数、字符串操作函数、字符操作函数、内存操作函数、时间/日期函数、数学函数、其他库函数;
💬 参照文档,学习几个库函数:
“strcpy - 字符串拷贝”

#include <stdio.h> #include <string.h> // Required Header; int main() { char arr1[20] = {0}; // strDestination; char arr2[] = "hello world"; // strSource; strcpy(arr1, arr2); printf("%s\n", arr1); return 0; }
🚩 >>> hello world
💬 参照文档,试着学习几个库函数:
“memset - 内存设置”

#include <stdio.h> #include <string.h> // Requested Header int main() { char arr[] = "hello world"; // dest memset(arr, 'x', 5); // (dest, c, count) printf("%s\n", arr); return 0; }
🚩 >>> xxxxx world
0x03 自定义函数
❓ 何为自定义函数?
“顾名思义,全部由自己设计,赋予程序员很大的发挥空间”
📚 自定义函数和其他函数一样,有函数名、返回值类型和函数参数;
1. ret_type 为返回类型;
2. func_name 为函数名;
3. paral 为函数参数;

💬 自定义函数的演示
“需求:写一个函数来找出两个值的较大值”
int get_max(int x, int y) { // 我们需要它返回一个值,所以返回类型为int; int z = 0; if (x > y) z = x; else z = y; return z; // 返回z - 较大值; } int main() { int a = 10; int b = 20; // 函数的调用; int max = get_max(a, b); printf("max = %d\n", max); return 0; }

🚩 >>> max = 20
0x04 函数的参数
📚 实际参数(实参)
1. 真实传给函数的参数叫实参(实参可以是常量、变量、表达式、函数等);
2. 无论实参是何种类型的量,进行函数调用时,必须有确定的值,以便把这些值传送给形参;
📚 形式参数(形参)
1. 形参实例化后相当于实参的一份临时拷贝,修改形参不会改变实参;
2. 形式参数只有在函数被调用的过程中才实例化;
3. 形式参数在函数调用完后自动销毁,只在函数中有效;
📌 注意事项:
1. 形参和实参可以同名;
2. 函数的形参一般都是通过参数压栈的方式传递的;
3. “形参很懒”:形参在调用的时才实例化,才会开辟内存空间;

0x05 函数的调用
📚 传值调用
1. 传值调用时,形参是实参的一份临时拷贝;
2. 函数的形参和实参分别占用不同内存块,对形参的修改不会影响实参;
3. 形参和实参使用的不是同一个内存地址;
📚 传址调用
1. 传址调用时可通过形参操作实参;
2. 传址调用是把函数外部创建的变量的内存地址传递给函数参数的一种调用函数的方式;
3. 使函数内部可以直接操作函数外部的变量(让函数内外的变量建立起真正的联系);
💬 交换两个变量的内容
// void,表示这个函数不返回任何值,也不需要返回; void Swap(int x, int y) { int tmp = 0; tmp = x; x = y; y = tmp; } int main() { int a = 10; int b = 20; // 写一个函数 - 交换2个整形变量的值 printf("交换前:a=%d b=%d\n", a, b); Swap(a, b); printf("交换后:a=%d b=%d\n", a, b); return 0; }

🚩 >>> 交换前:a=10 b=20 交换后:a=10 b=20
❓ “为何没有交换效果?是哪里出问题了吗?”
🔑 解析:Swap在被调用时,实参传给形参,其实形参是实参的一份临时拷贝。因为改变型形参并不能改变实参,所以没有交换效果;
💡 解决方案:使用传址调用(运用指针)
// 因为传过去的是两个整型地址,所以要用int*接收; void Swap2(int* pa, int* pb) { // 传址调用; int tmp = *pa; // *将pa解引用; *pa = *pb; *pb = tmp; } int main() { int a = 10; int b = 20; printf("交换前:a=%d b=%d\n", a, b); Swap2(&a, &b); // 传入的是地址; printf("交换后:a=%d b=%d\n", a, b); return 0; }

0x06 函数的嵌套调用
📚 函数和函数之间可以有机合成的;
void new_line() { printf("hehe "); } void three_line() { int i = 0; for (i=0; i<3; i++) new_line(); // three_line又调用三次new_line; } int main() { three_line(); // 调用three_line; return 0; }
🚩 >>> hehe hehe hehe
0x07 函数的链式访问
📚 把一个函数的返回值作为另外一个函数的参数
int main() { /* strlen - 求字符串长度 */ int len = strlen("abc"); printf("%d\n", len); printf("%d\n", strlen("abc")); // 链式访问 /* strcpy - 字符串拷贝 */ char arr1[20] = {0}; char arr2[] = "bit"; strcpy(arr1, arr2); printf("%s\n", arr1); printf("%s\n", strcpy(arr1, arr2)); // 链式访问 return 0; }

💭 面试题
“结果是什么?”
int main() { printf("%d", printf("%d", printf("%d", 43))); return 0; }
🚩 >>> 4321
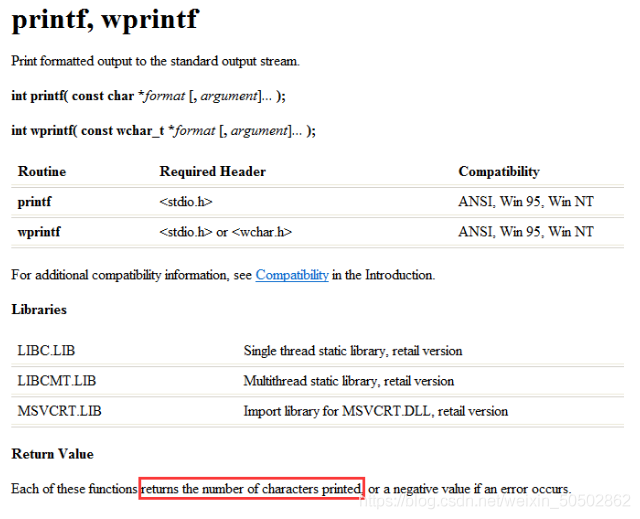
🔑 解析: printf函数的作用是打印,但是它也有返回值,printf的返回值是返回字符的长度;printf调用printf再调用printf("%d", 43),首先打印出43,返回字符长度2,打印出2,printf("%d", printf("%d", 43)) 又返回字符长度1,打印出1;所以为4321;
“我们可以试着再MSDN里查找printf函数的详细介绍”
0x08 函数的声明和定义
📚 函数的声明
1. 为了告诉编译器函数名、参数、返回类型是什么,但是具体是不是存在,无关紧要;
2. 函数必须保证“先声明后使用”,函数的声明点到为止即可;
3. 函数的声明一般要放在头文件中;
📚 函数的定义:是指函数的具体实现,交代函数的功能实现;
int main() { int a = 10; int b = 20; /* 函数的声明 */ int Add(int, int); int c = Add(a, b); printf("%d\n", c); return 0; } /* 函数的定义 */ int Add(int x, int y) { return x + y; }
二、函数的递归
0x00 递归的定义
📚 程序调用自身称为递归(recursion)
1. 递归策略只需要少量的程序就可以描述解题过程所需要的多次重复计算,大大减少代码量;
2. 递归的主要思考方式在于:把大事化小;
📌 注意事项:
1. 存在跳出条件,每次递归都要逼近跳出条件;
2. 递归层次不能太深,避免堆栈溢出;

💬 递归演示
“接收一个整型值,按照顺序打印它的每一位(eg. 输入1234,输出 1 2 3 4)”
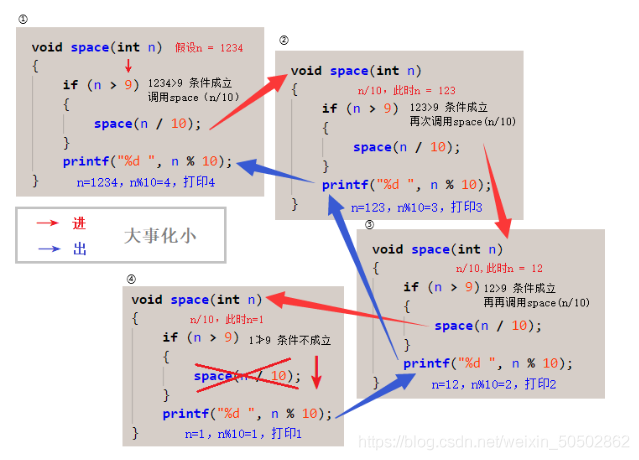
void space(int n) { if (n > 9) { space(n / 10); } printf("%d ", n % 10); } int main() { int num = 1234; space(num); return 0; }

🚩 >>> 1 2 3 4
🔑 解析:
0x01 堆栈溢出
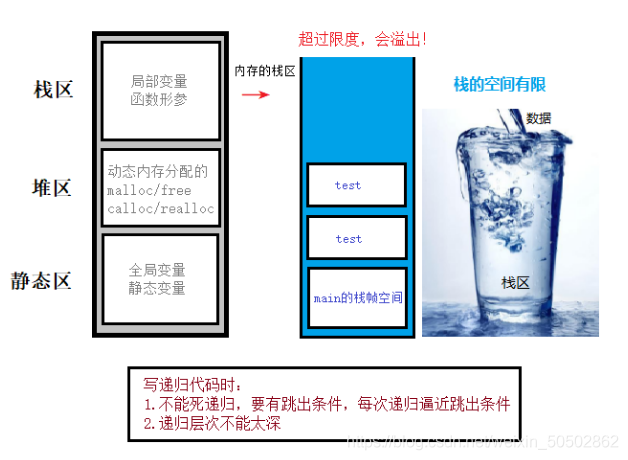
📚 堆栈溢出现象 - stackoverflow
1. 水满则溢,堆栈也有容量限制,当其超出限制,就会发生溢出;
2. 堆栈溢出可以理解为“吃多了吐”,队列溢出就是“吃多了拉”;
3. 程序员的知乎:Stack Overflow - Where Developers Learn, Share, & Build Careers
💀 危害:
1. 堆栈溢出时会访问不存在的RAM空间,造成代码跑飞,此时无法获取溢出时上下文数据,也无法对后续的程序修改提供有用信息;
2. 造成安全威胁,常见的攻击类型有:修改函数的返回地址,使其指向攻击代码,当函数调用结束时程序跳转到攻击者设定的地址,修改函数指针,长跳转缓冲区来找到可溢出的缓冲区;
💬 堆栈溢出现象演示;
void test(int n) { if(n < 10000) { test(n + 1); } } int main() { test(1); return 0; }
0x02 递归的用法
💬 手写strlen函数
1. “创建临时变量count方法”
int my_strlen(char* str) { int count = 0; while (*str != '\0') { count++; str++; } return count; } int main() { char arr[] = "abc"; int len = my_strlen(arr); // 传过去的是首素地址; printf("len = %d\n", len); return 0; }

🚩 >>> len = 3
2. “不创建临时变量,利用递归完成”
/* my_strlen("abc"); 1 + my_strlen("bc"); 1 + 1 + my_strlen("c"); 1 +1 + 1 + my_strlen(""); 1 + 1 + 1 + 0 3 */ int rec_strlen(char* str) { if (*str != '\0') return 1 + rec_strlen(str+1); else return 0; } int main() { char arr[] = "abc"; int len = rec_strlen(arr); printf("len = %d\n", len); return 0; }

🚩 >>> len = 3
0x03 递归与迭代
❓ 何为迭代:
“重复执行程序中的循环,直到满足某条件时才停止,亦称为迭代”
📚 迭代法:也称辗转法,是一种不断用变量的旧值递推新值的过程;
💬 求n的阶乘(不考虑溢出);
“阶乘公式: n! = n(n-1)”
int Fac(int n) { if (n <= 1) return 1; else return Fac(n-1) * n; } int main() { int n = 0; scanf("%d", &n); int ret = Fac(n); printf("%d\n", ret); return 0; }

💬 求第n个斐波那契数(不考虑溢出);
“斐波拉契数列:0,1,1,2,3,5,8,13,21,34,55...”

int Fib(int n) { if (n <= 2) return 1; else return Fib(n-1) + Fib(n-2); } int main() { int n = 0; scanf("%d", &n); int ret = Fib(n); printf("第%d个斐波拉契数为%d\n", n, ret); return 0; }

🚩 >>> (假设输入10) 第10个斐波那契数为55
>>> (假设输入20)第20个斐波那契数为6765
>>> (假设输入50)...(程序运行中,似乎卡住了)
0x04 非递归
❓ 我们发现了问题,如果用Fib这个函数计算第50个斐波那契数字的时候需耗费很长的时间;
使用Fic函数求10000的阶乘(不考虑结果的正确性),程序会崩溃;
🔑 耗费很长时间的原因是 Fib函数在调用的过程中很多计算其实在一直重复,比如计算第50个斐波那契数就要计算第49个,计算第49个斐波那契数就要计算第48个……以此类推;
💡 优化方法:将递归改写为非递归;
📜 箴言:
1. 许多问题是以递归的形式进行解释的,这只是因为他比非递归的形式更为清晰;
2. 但是这些问题的迭代实现往往比递归实现效率更高,虽然代码的可读性稍微差些;
3. 当一个问题相当复杂,难以用迭代实现时,此时递归实现的简洁性便可以补偿运行时开销;
💬 使用非递归的方式写;
1 1 2 3 5 8 13 21 34 55...
a b c
int Fib(int n) { int a = 1; int b = 1; int c = 1; while (n > 2) { c = a + b; a = b; b = c; n--; } return c; } int main() { int n = 0; scanf("%d", &n); int ret = Fib(n); printf("%d\n", ret); return 0; }

💬 非递归方式求阶乘
int fac(int n) { int ret = 1; while(n > 1) { ret *= n; n -= 1; } return ret; } int main() { int n = 0; scanf("%d", &n); int ret = fac(n); printf("%d\n", ret); return 0; }

三、练习
0x00 练习1
1. 写一个函数可以判断一个数是不是素数;
2. 写一个函数判断一年是不是闰年;
3. 写一个函数,实现一个整形有序数组的二分查找;
4. 写一个函数,每调用一次这个函数,就会将num的值增加1;
💬 写一个is_prime()函数可以判断一个数是不是素数;
“质数是指在大于1的自然数中,除了1和它本身以外不再有其他因数的自然数。”
#include <stdio.h> int is_prime(int n) { int i = 0; for(i=2; i<n; i++) { if(n % i == 0) return 0; } if(i == n) return 1; else return 0; } int main() { int n = 0; scanf("%d", &n); int ret = is_prime(n); if(ret == 1) { printf("%d是素数\n", n); } else { printf("%d不是素数\n", n); } return 0; }

💬 写一个 is_leap_year 函数判断一年是不是闰年;
int is_leap_year(int y) { if((y % 4 == 0) && (y % 100 != 0) || (y % 400 == 0)) return 1; else return 0; } int main() { int year = 0; printf("请输入年份: "); scanf("%d", &year); if(is_leap_year(year) == 1) printf("%d年是闰年\n", year); else printf("不是闰年\n"); return 0; }

💬 写一个函数,实现一个整形有序数组的二分查找;
“ int arr[] = {1,2,3,4,5,6,7,8,9,10}; ”
int binary_search(int arr[], int k, int sz) { int left = 0; int right = sz - 1; while(left <= right) { int mid = (left + right) / 2; if(arr[mid] < k) left = mid + 1; else if(arr[mid] > k) right = mid - 1; else return mid; } return -1; } int main() { int arr[] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}; int sz = sizeof(arr) / sizeof(arr[0]); int k = 0; printf("请输入要查找的值: "); scanf("%d", &k); int ret = binary_search(arr, k, sz); if(ret == -1) printf("找不到\n"); else printf("找到了,下标为%d\n", ret); return 0; }

💬 写一个函数,每调用一次这个函数,就会将num的值增加1;
void Add(int* pnum) { (*pnum)++; } int main() { int num = 0; Add(&num); printf("%d\n", num); Add(&num); printf("%d\n", num); Add(&num); printf("%d\n", num); return 0; }

🚩 >>> 1 2 3
0x01练习2
1. 实现一个函数,判断一个数是不是素数,利用上面实现的函数打印100到200之间的素数;
2. 交换两个整数,实现一个函数来交换两个整数的内容;
3. 自定义乘法口诀表,实现一个函数,打印乘法口诀表,口诀表的行数和列数自己指定;
💬 实现一个函数,判断一个数是不是素数;
“利用上面实现的函数打印100到200之间的素数,打印出一共有多少个素数”
int is_prime(int n) { int j = 0; for(j=2; j<n; j++) { if(n % j == 0) return 0; } return 1; } int main() { int i = 0; int count = 0; for(i=100; i<=200; i++) { if(is_prime(i) == 1) { count++; printf("%d ", i); } } printf("\n一共有%d个素数", count); return 0; }
🚩 >>> 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 一共有21个素数
💬 交换两个整数;
“实现一个函数来交换两个整数的内容”
void Swap(int* pa, int* pb) { int tmp = 0; tmp = *pa; *pa = *pb; *pb = tmp; } int main() { int a = 10; int b = 20; printf("交换前: a=%d, b=%d\n", a, b); Swap(&a, &b); printf("交换后: a=%d, b=%d\n", a, b); return 0; }

🚩 >>> 交换前: a=10, b=20 交换后: a=20, b=10
自定义乘法口诀表;
“实现一个函数,打印乘法口诀表,口诀表的行数和列数自己指定”
(eg.输入9,输出9*9口诀表,输出12,输出12*12的乘法口诀表。)
void formula_table(int line) { int i = 0; for(i=1; i<=line; i++) { int j = 0; for(j=1; j<=i; j++) { printf("%dx%d=%-2d ", j, i, i*j); } printf("\n"); } } int main() { int line = 0; printf("请定义行数: > "); scanf("%d", &line); formula_table(line); return 0; }

0x02 练习3
1. 字符串逆序,非递归方式的实现和递归方式的实现;
2. 写一个函数DigitSum(n),输入一个非负整数,返回组成它的数字之和;
3. 编写一个函数实现n的k次方,使用递归实现;
💬 字符串逆序
编写一个函数 reverse_string(char * string);
将参数字符串中的字符反向排列,不是逆序打印;
要求:不能使用C函数库中的字符串操作函数;
(eg. char arr[] = "abcdef"; 逆序之后数组的内容变成:fedcba)
非递归实现:
int my_strlen(char* str) { if(*str != '\0') { return 1 + my_strlen(str + 1); } return 0; } void reverse_string(char* str) { int len = my_strlen(str); int left = 0; int right = len - 1; while(left < right) { char tmp = str[left]; str[left] = str[right]; str[right] = tmp; left++; right--; } } int main() { char arr[] = "abcdef"; reverse_string(arr); printf("%s\n", arr); return 0; }

🚩 >>> fedcba
递归实现:
1. [] 写法
int my_strlen(char* str) { int count = 0; while(*str != '\0') { count++; str++; } return count; } void reverse_string(char *str) { int len = my_strlen(str); int left = 0; // 最左下标 int right = len - 1; // 最右下标 char tmp = str[left]; str[left] = str[right]; str[right] = '\0'; // 判断条件 if(my_strlen(str + 1) >= 2) { reverse_string(str + 1); } str[right] = tmp; } int main() { char arr[] = "abcdef"; reverse_string(arr); printf("%s\n", arr); return 0; }

2. *写法
int my_strlen(char* str) { if(*str != '\0') { return 1 + my_strlen(str + 1); } return 0; } void reverse_string(char* str) { int len = my_strlen(str); char tmp = *str; *str = *(str + len-1); *(str + len-1) = '\0'; if(my_strlen(str + 1) >= 2) { reverse_string(str + 1); } *(str + len-1) = tmp; } int main() { char arr[] = "abcdef"; reverse_string(arr); printf("%s\n", arr); return 0; }

💬 写一个递归函数DigitSum(n),输入一个非负整数,返回组成它的数字之和;
“调用DigitSum(1729),则应该返回1+7+2+9,它的和是19”(eg. 输入:1729,输出:19)
int digit_sum(int n) { if (n > 9) { return digit_sum(n / 10) + (n % 10); } else { return 1; } } int main() { int n = 1729; int ret = digit_sum(n); printf("%d\n", ret); return 0; }

🚩 >>> 19
🔑 解析:
digit_sum(1729)
digit_sum(172) + 9
digit_sum(17) + 2 + 9
digit_sum(1) + 7 + 2 + 9
1+7+2+9 = 19
💬 编写一个函数实现n的k次方,使用递归实现
“递归实现n的k次方”
double Pow(int n, int k) { if (k == 0) return 1.0; else if(k > 0) return n * Pow(n, k-1); else // k < 0 return 1.0 / (Pow(n, -k)); } int main() { int n = 0; int k = 0; scanf("%d^%d", &n, &k); double ret = Pow(n, k); printf("= %lf\n", ret); return 0; }

🚩 >>> (假设输入 2^3)8.000000 (假设输入 2^-3)0.
🔑 解析:
1. k=0,结果为1;
2. k>0,因为n的k次方等同于n乘以n的k次方-1,可以通过这个“大事化小”;
3. k<0,k为负指数幂时可化为 1 / n^k


版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/bian-cheng-ji-chu/92662.html