高数基础02_定积分&多元函数

一、定积分

1、定义

一、定积分

定积分用于求解函数在某个区间上的累积效应或面积。

1、定义

$\int_{a}^{b}f(x)dx$

表示函数 f(x)在区间 [a,b]上的累积效应或面积。

通过极限推导：

2、几何意义

$\int_{a}^{b}f(x)dx$ 的几何意义是函数 f(x) 在区间 [a,b]上的曲线下面积：

如果 f(x)≥0，则定积分表示曲线下方的面积。
如果 f(x)≤0，则定积分表示曲线上方的面积的负值。

3、性质

线性性质
区间可加性
积分上下限交换
定积分中值定理：

如果函数 f(x) 在闭区间 [a,b] 上连续，则存在 c∈[a,b]，使得：

$\int_{a}^{b}f(x)dx= f(c)(b-a)$

（证明方法：连续函数的介值定理）

4、基本公式

牛顿-莱布尼茨公式

$\int_{a}^{b}f(x)dx= F(b)-F(a)$

其中，F(x)是 f(x)的一个原函数，即 F′(x)=f(x)

微积分基本定理

如果 f(t) 在区间 [a,b]上连续，则积分上限函数 $F(x)=\int_{a}^{x}f(t)dt$ 在区间 [a,b] 上可导，并且其导数为：
如果 F(x)是 f(x)的一个原函数，即 F′(x)=f(x)，则： $\int_{a}^{b}f(x)dx=F(b)-F(a)$

5、换法

$\int_{a}^{b}f(x)dx=\int_{a}^{b}f(\phi (t))\phi' (t)dt$

令t = g(x)，则有x = $g^{-1}(x)$ = $\phi (t)$

dx = $\phi' (t)dt$ ，代入即可。

二、多函数

1、二极限

1.1定义

设函数 f(x,y) 在点 (a,b) 的某个去心邻域内有定义。如果对于任意给定的正数 ϵ，总存在正数 δ，使得当 $0<\sqrt{(x-a)^{2}+(y-b)^{2}}< \delta$ 时，总有： ∣f(x,y)−L∣<ϵ，则称 L 为函数 f(x,y)在点 (a,b)处的极限，记作：

$\lim_{(x,y)\rightarrow (a,b)}f(x,y)= L$

1.2几何意义

当点 (x,y)从任意方式趋近于点 (a,b) 时，函数 f(x,y) 的值趋近于 L。

如果 (x,y)从不同方式趋近于点 (a,b)，函数 f(x,y) 的值不相等，则表示 f(x,y) 不存在。

2、偏导数

偏导数表示在多个自变量中，当其中一个自变量改变而其他自变量保持不变时函数值的变化率。

实质上是将其他自变量视为常数，然后按照单变量函数求导的方法进行运算。

定义

设函数 f(x,y) 在点 (x0,y0) 的某个邻域内有定义。如果极限：

存在，则称此极限为函数 f(x,y)在点 (x0,y0) 处对 x 的偏导数，记作：

类似地，如果极限：

存在，则称此极限为函数 f(x,y)在点 (x0,y0)处对 y的偏导数，记作：

计算方法

对于二函数z=f(x,y)，求z对x的偏导数时，将y看作常量，对x求导；求z对y的偏导数时，将x看作常量，对y求导。

3、全微分

定义

如果函数z=f(x, y)在点(x, y)处的全增量

可以表示为

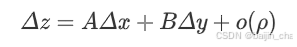
其中A、B不依赖于Δx, Δy，仅与x, y有关，ρ趋近于0(ρ=√[(Δx)²+(Δy)²])，此时称函数z=f(x, y)在点(x, y)处可微分，AΔx+BΔy称为函数z=f(x, y)在点(x, y)处的全微分，记为dz即dz=AΔx +BΔy。

可微的必要条件条件

若z=f(x,y)在(x,y)点处可微，则偏导数 $f_{x}^{'}(x,y)$ 和 $f_{y}^{'}(x,y)$ 存在，并且

可微的充分条件

z=f(x,y)在(x,y)的某个邻域内有连续的偏导数 $f_{x}^{'}(x,y)$ 和 $f_{y}^{'}(x,y)$ ，则在(x,y)处可微。

近似计算

z=f(x, y)在点(x, y)处的全增量为

在计算中我们通常使 $\Delta z\approx dz$ ，所以

即得到近似计算公式：

4、梯度

梯度是一个向量，表示多函数在某一点处的最大变化率和变化方向。

4.1定义

设 f(x1,x2,…,xn)是一个定义在 Rn(n维欧几里得空间) 上的多函数，函数 f在n维向量点 a=(a1,a2,…,an)处的梯度定义为：

其中 $\frac{\partial f}{\partial x{_i}}(a)$ 是函数 f 在点 a 处对第 i 个自变量的偏导数。

4.2性质

最大变化率：梯度 ∇f(a) 的方向是函数 f在点 a 处变化率最大的方向。
变化率：梯度 ∇f(a) 的大小（模）是函数 f 在点 a 处沿梯度方向的变化率。

沿梯度方向是是函数 f 在点 a 处变化率增加最大的方向；沿梯度反方向是是函数 f在点 a 处变化率减小最大的方向；沿梯度垂直方向函数 f在点 a 处变化率为0。

4.3梯度下降

梯度下降是一种优化算法，用于寻找多函数的最小值。其基本思想是沿着函数的负梯度方向逐步更新参数，以减少函数值。

算法步骤

初始化：选择一个初始点 x0。
迭代更新：对于每次迭代 k，计算当前点的梯度，并更新参数：

其中，η 是学习率（步长），控制每次更新的步幅。

终止条件：当梯度的模足够小或达到预设的迭代次数时，停止迭代。通常，终止条件可以是以下几种：梯度的模足够小、达到预设的迭代次数、函数值变化足够小 。

5、二重积分

二重积分是多微积分中的一个重要概念，用于计算二维区域上的函数积分。它通常用于计算平面区域上的面积、质量、重心等问题。

二重积分的基本思想是将一个二维区域分割成无数个小区域，然后在每个小区域上计算函数值的积分。

5.1定义

设 f(x,y)f(x,y) 是定义在平面区域 D 上的函数，二重积分记作： $\iint_{D}^{}f(x,y)dA$ ，其中 dA表示面积素。

5.2几何意义

如果 f(x,y)是非负函数，二重积分 $\iint_{D}^{}f(x,y)dA$ 表示以 D 为底、以 f(x,y)为顶的曲顶柱体的体积。

5.3二重积分的计算-直角坐标系

在直角坐标系下，二重积分可以表示为两个定积分的乘积：

其中 D 是由 x=a 到 x=b 以及 y=g(x)到 y=h(x) 围成的区域。

5.4二重积分的计算-极坐标系

极坐标系的二重积分计算需要将直角坐标系的坐标转换为极坐标。

极坐标系的基本概念

原点：极坐标系的原点称为极点（通常记作 O）。
极径：从极点到某一点的距离称为径向距离（通常记作 r）。
极角：从极点到某一点的射线与极轴（通常是正 xx 轴）之间的角度称为极角（通常记作 θ）。

给定点的极坐标 (r,θ)，可以转换为直角坐标 (x,y)： $x=r\cos\theta \\ y=r\sin\theta$

在极坐标下，二重积分的表达式为：

其中 r 和 θ 分别是极径和极角。

今天的文章高数基础02_定积分&多函数分享到此就结束了，感谢您的阅读。

高数基础02_定积分&多元函数

一、定积分

1、定义

2、几何意义

3、性质

4、基本公式

5、换法

二、多函数

1、二极限

1.1定义

1.2几何意义

2、偏导数

3、全微分

4、梯度

4.1定义

4.2性质

4.3梯度下降

5、二重积分

5.1定义

5.2几何意义

5.3二重积分的计算-直角坐标系

5.4二重积分的计算-极坐标系

相关推荐