prim算法（prim算法求最小生成树代码）

最小生成树的概念：

最小生成树是基于“带权图” 的，即图中每条边上都有特定的权值，这样的图又称为网。最小生成树指的是所有生成树中，权值之和最小的树。

Prim算法：

假设G=(V,E)为一网图，其中V为顶点的集合，E为边的集合。从某一顶点u1出发，选择与它关联的具有最小权值的边(u1, v)，将其顶点v加入到生成树顶点

集合U中。U用于存放G的最小生成树中的顶点，T存放G的最小生成树中的边。

令集合U的初值为U={u1} (假设构造最小生成树时，从顶点u1出发)，集合T的初值为T={ }。

以后每一步从U中选择一个顶点u（u属于U），而另一个顶点v属于V-U的边中，选取具有最小权值的边（u，v），将顶点v加入集合U中，将边（u,v）加入集合T

中，如此不断重复，直到U=V时，最小生成树构造完毕，这时集合T中包含了最小生成树的所有边。

Prim算法的描述：

（1）U={u1} , T={ }

(2) while(U<>V)

(u,v)=min{W_uv; u属于U, v属于V-U};

T=T+{ (u, v) };

U=U + { v }.

(3) 结束

在构造过程中，设置了两个辅助数组：lowcost[]存放生成树顶点集合U内顶点到生成树外V-U各顶点的各边上的当前最小权值；

nearvex[]记录生成树顶点集合外各顶点距离集合内哪个顶点最近（即权值最小）.

若选择从顶点0出发，即u₀=0, 则两个辅助数组的初始状态为：

反复做以下工作：

（1）在lowcost[ ]中选择nearvec[ ]<>-1 && lowcost[i]最小的边，用v标记它。则选中的权值最小的边为(nearvex[v] , v)，相应的权值为lowcost[v]。

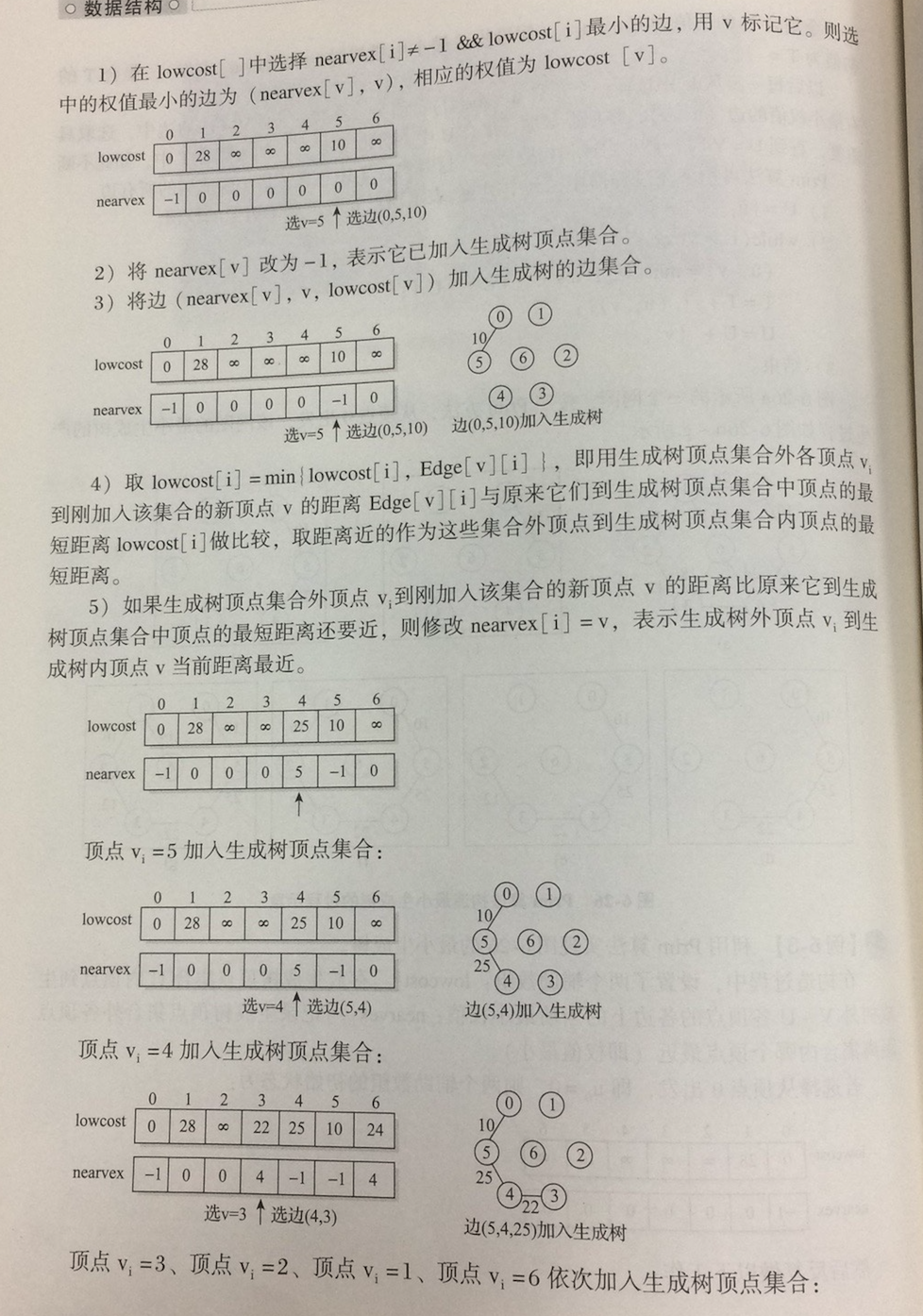
程序如下：

// main.cpp

// Prim

// Created by duanqibo on 2019/7/3.

// Prim普利姆算法建立最小生成树

#include <iostream>

#include <stdio.h>

#define MaxVerNum 100

#define MaxValue 10000

typedef struct{

char vexs[MaxVerNum]; //顶点集合

int edges[MaxVerNum][MaxVerNum]; //边集合

int n,e; //顶点和边

}MGraph;

char vertex[]="0";

int nvertex=7,nedges=9;

int connection[][3]={{0,1,28},{0,5,10},{1,2,16},{1,6,14},{2,3,12},{3,4,22},{3,6,18},{4,5,25},{4,6,24}};

void CreateMgraph(MGraph &G)

{

int i,j,k;

G.n=nvertex;

G.e=nedges;

for(i=0;i<G.n;i++)

G.vexs[i]=vertex[i]; //顶点

for(i=0;i<G.n;i++)

for(j=0;j<G.n;j++)

G.edges[i][j]=MaxValue; //初始化边最大值，没有边

for(i=0;i<G.n;i++)

G.edges[i][i]=0; //初始化边为0

for(k=0;k<G.e;k++)

{

i=connection[k][0];

j=connection[k][1];

G.edges[i][j]=connection[k][2];

G.edges[j][i]=G.edges[i][j]; //有向图没有这一行

}

void printMgraph(MGraph &G)

{

int i,j;

printf("图的结点总数：%d 边总数：%d ",G.n,G.e);

for(i=0;i<G.n;i++)

{

for(j=0;j<G.n;j++)

if(G.edges[i][j]==10000)

printf("∞ "); //"00"代表无穷

else

printf("%d ",G.edges[i][j]);

printf(" ");

}

//最小生成树

typedef struct

{

int head,tail,cost;

}MST[MaxVerNum];

void Prim(MGraph &G,MST &T,int u)

{

int i,j;

int *lowcost=new int[G.n];

int *nearvex=new int[G.n];

for(i=0;i<G.n;i++)

{

lowcost[i]=G.edges[u][i]; //u到各点的代价

nearvex[i]=u; //最短带权路径

}

nearvex[u]=-1; //加入到生成树顶点集合

int k=0;

for(i=0;i<G.n;i++)

if(i!=u)

{

int min=MaxValue;

int v=u;

for(j=0;j<G.n;j++)

if(nearvex[j]!=-1 && lowcost[j]<min) //=-1不参选

{

v=j;

min=lowcost[j];//求生成树外顶点到生成树内顶点具有最小权值的边，

//v是当前具有最小权值的边

}

if(v!=u)

{

T[k].tail=nearvex[v];

T[k].head=v;

T[k++].cost=lowcost[v];

nearvex[v]=-1; //该边加入生成树标记

for(j=0;j<G.n;j++)

if(nearvex[j]!=-1 && G.edges[v][j]<lowcost[j])

{

lowcost[j]=G.edges[v][j]; //修改

nearvex[j]=v;

}

}//循环n-1次，加入n-1条边

}

int main(int argc, const char * argv[]) {

int i;

MGraph g;

CreateMgraph(g);

printMgraph(g);

MST t;

Prim(g,t,0);

printf("生成树：结点->权值->结点 ");

for(i=0;i<g.n;i++)

printf("(%d)-->%d-->(%d) ",t[i].tail,t[i].cost,t[i].head);

return 1;

}

运行结果如下：

今天的文章 prim算法（prim算法求最小生成树代码）分享到此就结束了，感谢您的阅读。

prim算法（prim算法求最小生成树代码）

相关推荐