基于奇异值分解的图像压缩和信息隐藏
将图像进行奇异值分解后,通过对对角矩阵进行一系列操作,可以达到压缩图像以及信息隐藏的目的。不仅如此,随着计算机网络和网络技术的不断发展,数字图像、音频和视频产品越来越需要一种有效的版权保护方案。利用奇异值分解实现数字图像水印技术,将水印图片置乱再隐写入图像的方法可以在一定程度上避免被破译;为了进一步防止破译,结合离散余弦变化以及奇异值分解的数字水印技术更加安全。
基于奇异值分解的图像压缩
灰度图
一张灰度图是由m*n的矩阵构成的,矩阵的每一个元素是处于0~255的整数,每一个元素就代表着对应像素点的灰度。而一张彩色图像可以转化为灰度图rgb2gray(),即一个非负矩阵A。
奇异值分解
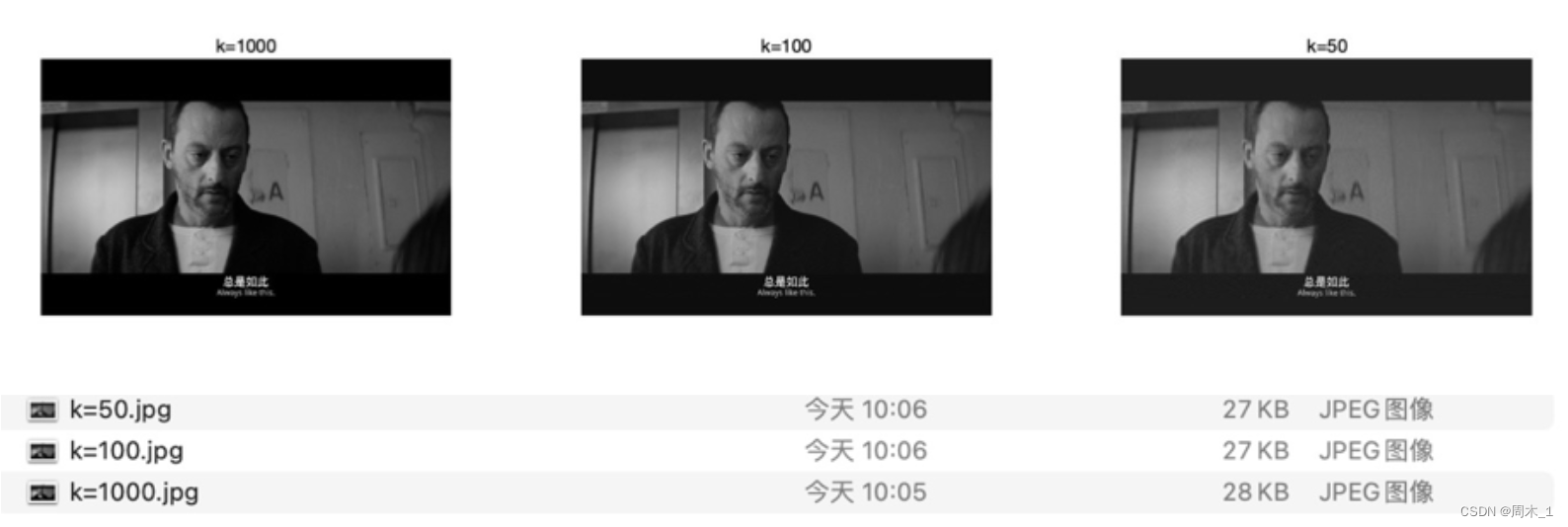
奇异值分解svd()可以理解为利用正交向量的性质,将矩阵A包含的**“信息空间”分解为r个相互正交的“子信息空间”,每一个“子信息空间”中都包含了一定的原图像信息。相应的,删除k个“子信息空间”可以达到降维的目的,k取合适的值时,人类肉眼无法清楚分辨是否有信息损失,就可以达到兼顾保留图像信息和压缩图像文件大小**的目的。
矩阵A的奇异值分解定义如下:
A = U S V T A=USV^T A=USVT
具体步骤是:
- 奇异值分解矩阵A,得到正交矩阵U、V和对角矩阵S
- 取出矩阵U、V的前k行数据,构成 U 1 , V 1 U_1, V_1 U1,V1,S化为** k × k k \times k k×k的对角矩阵** S 1 S_1 S1。
A 1 = U 1 S 1 V 1 T A_1=U_1S_1V_1^T A1=U1S1V1T
clear;
% 使用SVD压缩图像
%% k=1000
k = 1000;
img = double(rgb2gray(imread("Always like this.png")));
[U, S, V] = svd(img);
U_1 = U(:, 1:k);
SS = diag(S);
SSS = SS(1:k);
S_1 = diag(SSS);
V_1 = V(:, 1:k);
img_1000 = U_1*S_1*V_1';
figure(1);
subplot(1, 3, 1);
imshow(mat2gray(img_1000));
title('k=1000');
%% k=100
k = 100;
U_2 = U(:, 1:k);
SSS = SS(1:k);
S_2 = diag(SSS);
V_2 = V(:, 1:k);
img_100 = U_2*S_2*V_2';
subplot(1, 3, 2);
imshow(mat2gray(img_100));
title('k=100');
%% k=50
k = 50;
U_3 = U(:, 1:k);
SSS = SS(1:k);
S_3 = diag(SSS);
V_3 = V(:, 1:k);
img_50 = U_3*S_3*V_3';
subplot(1, 3, 3);
imshow(mat2gray(img_50));
title('k=50');
代码运行结果:
基于奇异值分解的数字图像水印
将SVD应用于数字图像水印技术的主要理论背景是:
- 图像的奇异值稳定性非常好,即当图像被施加小的扰动时,图像的奇异值不会有太大的变化;
- 奇异值所表现的是图像的内蕴特性而非视觉特性。
具体步骤:
- 将图像A奇异值分解,得到$ U、S、V $
- 将水印$ W\in R_{n\times n} 叠 加 到 对 角 矩 阵 叠加到对角矩阵 叠加到对角矩阵 S $ 上,$ S+ \alpha W $
- 对$ S+ \alpha W 进 行 奇 异 值 分 解 , 得 到 进行奇异值分解,得到 进行奇异值分解,得到 U, S_1, V_1^T $
- 将$ U, S_1, V^T $相乘,就可以得到包含水印的图像
A = > U S V T A => USV^T A=>USVT
S + α W = > U 1 S 1 V 1 T S+\alpha W => U_1S_1V_1^T S+αW=>U1S1V1T
A ^ = U S 1 V T \hat{A}=US_1V^T A^=US1VT
如果想要提取水印,则只需要进行简单的求逆,再次不多赘述。
生成水印图
此处的水印图我使用的是二维码,采用Python中qrcode库生成。
import qrcode
qr = qrcode.QRCode(
version = 2,
box_size = 8,
border = 0
)
qr.make('Life is fantastic')
img = qr.make_image();
with open('watermark.png', 'wb') as f:
img.save(f)
Arnold置乱
Arnold置乱(也称作cat置乱)可以对图像进行置乱,使得原本有意义的图像变成一张无意义的图像。其矩阵变换公式是:
( x 1 y 1 ) = [ 1 1 1 2 ] ( x y ) m o d ( N ) \begin{pmatrix}x_1\\y_1\\\end{pmatrix}=\begin{bmatrix} 1&1\\1&2\\\end{bmatrix}\begin{pmatrix}x\\y\\\end{pmatrix}mod(N) (x1y1)=[1112](xy)mod(N)
其中mod是取模运算,N是正方形图像的边长, ( x 1 , y 1 ) (x_1, y_1) (x1,y1)是 ( x , y ) (x, y) (x,y)变换之后的坐标位置。
对于图像而言,这里的位置移动,实际上是对应点的灰度值或者RGB值的移动,即将原来 ( x , y ) (x, y) (x,y)的灰度值或者RGB颜色分量移动到 ( x 1 , y 1 ) (x_1, y_1) (x1,y1)如果对一个数字图像迭代地使用离散化的Arnold变换,即将左端输出的 ( x 1 , y 1 ) (x_1, y_1) (x1,y1)作为下一次Arnold变换的输入,则可以重复这个过程一直做下去。当迭代到某一步时,如果出现的图像呈现出杂乱无章、无法辨识的情况,那么就得到了一幅置乱图。
相应的反变换公式如下:
( x 2 y 2 ) = [ 2 − 1 − 1 1 ] ( x 1 y 1 ) m o d ( N ) \begin{pmatrix}x_2\\y_2\\\end{pmatrix}=\begin{bmatrix} 2&-1\\-1&1\\\end{bmatrix}\begin{pmatrix}x_1\\y_1\\\end{pmatrix}mod(N) (x2y2)=[2−1−11](x1y1)mod(N)
水印插入
为了提高加密程度,我们在插入水印之前先对水印图像进行预处理,即对它进行Arnold置乱,然后再执行基于奇异值分解的数字水印插入。
clear;
%% 图片预处理以及将水印图片加密进目标图片
% 首先将目标图像转化为灰度图
img = imread('Always like this.png');
watermark = double(imread('watermark.jpg'));
img_grayed = double(rgb2gray(img));
imwrite(uint8(img_grayed), 'AlwaysLikeThis_grayed.jpg');
figure(1);
subplot(2, 3, 1);
imshow(uint8(img_grayed));
title("原始图像");
subplot(2, 3, 2);
imshow(watermark);
title("原始水印");
key = 10; % key是对watermark进行Arnold置乱的次数
a = 3;b = 5;
[prow, pcol] = size(img_grayed);
[wrow, wcol] = size(watermark);
% 进行arnold置乱
watermark_arnolded = zeros(wrow, wcol);
for i = 1:key
for y = 1:wrow
for x = 1:wcol
xx = mod((x-1)+b*(y-1), wrow)+1;
yy = mod(a*(x-1)+(a*b+1)*(y-1), wrow)+1;
watermark_arnolded(yy, xx) = watermark(y, x);
end
end
watermark = watermark_arnolded;
end
subplot(2, 3, 3);
imshow(watermark_arnolded);
title("arnold置乱后的watermark");
% 对原始图像进行奇异值分解
[U, S, V] = svd(img_grayed);
S_copy = S;
alpha = 0.1; % 叠加强度
for i = 1:wrow
for j = 1:wcol
S(i, j) = S(i, j) + alpha * watermark_arnolded(i, j);
end
end
[U_1, S_1, V_1] = svd(S);
img_watered = U*S_1*V';
subplot(2, 3, 4);
imshow(uint8(img_watered));
title("添加水印的图像");
%% 将水印图片提取
[U_2, S_2, V_2] = svd(img_watered);
D = U_1 * S_2 * V_1';
watermark_res = zeros(wrow, wcol);
for i = 1:wrow
for j = 1:wcol
watermark_res(i, j) = (1/alpha)*(D(i, j) - S_copy(i, j));
end
end
subplot(2, 3, 5);
imshow(watermark_res);
title('提取出的watermark');
% 还原watermark
watermark_recovery = zeros(wrow, wcol);
for i = 1:key
for y = 1:wrow
for x = 1:wcol
xx=mod((a*b+1)*(x-1)-b*(y-1), wrow)+1;
yy=mod(-a*(x-1)+(y-1), wrow)+1;
watermark_recovery(yy, xx) = watermark_res(y, x);
end
end
watermark_res = watermark_recovery;
end
subplot(2, 3, 6);
imshow(watermark_recovery);
title("还原提取出的watermark");
代码运行结果:
基于离散余弦变换和奇异值分解的数字水印技术
离散余弦变换(DCT)
离散余弦变换 DCT是数据通信中最常用到的 变换编码的方法。图像经过DCT变换后其系数有较 好的感觉容量,利用此特点可以将水印信息嵌入到 DCT系数中,而不会引起图像质量的较大改变。
DCT系数分为直流分量和交流分量。直流分量 代表图像的亮度值,交流分量又分为高频带,中频带 和低频带。高频系数一般很小,人眼对高频部分失真 不太敏感,在图像做Jpeg等压缩处理时会将高频部分 舍弃,若在高频嵌入水印鲁棒性会降低,所以一般选 择将水印嵌入低频中。低频是数据块中能量集中区 域,也就是说经过DCT变换后,图像的大部分重要信 息都集中在DCT的低频系数里,所以在嵌入水印是 要控制好强度否则会造成图像质量下降。
二维离散余弦变换公式:
F ( u , v ) = c ( u ) c ( v ) ∑ x = 0 N − 1 ∑ y = 0 N − 1 f ( x , y ) c o s ( 2 x + 1 2 N u π ) c o s ( 2 y + 1 2 N v π ) x , y , u , v = 0 , 1 , . . . , N − 1 c ( u ) = c ( v ) = { 1 2 u = 0 , v = 0 1 其 他 F(u, v)=c(u)c(v)\sum_{x=0}^{N-1}\sum_{y=0}^{N-1}f(x, y)cos(\frac{2x+1}{2N}u\pi)cos(\frac{2y+1}{2N}v\pi)\ \ \ \ x,y,u,v=0,1,…,N-1 \\ c(u)=c(v)=\begin{cases} \frac{1}{\sqrt{2}}\ \ u=0,v=0\\ 1 \ \ 其他 \end{cases} F(u,v)=c(u)c(v)x=0∑N−1y=0∑N−1f(x,y)cos(2N2x+1uπ)cos(2N2y+1vπ) x,y,u,v=0,1,...,N−1c(u)=c(v)={
21 u=0,v=01 其他
二维离散余弦逆变换公式:
f ( x , y ) = 2 N ∑ u = 0 N − 1 ∑ v = 0 N − 1 F ( u , v ) c o s ( 2 x + 1 2 N u π ) c o s ( 2 y + 1 2 N v π ) x , y , u , v = 0 , 1 , . . . , N − 1 c ( u ) = c ( v ) = { 1 2 u = 0 , v = 0 1 其 他 f(x, y)=\frac{2}{N} \sum_{u=0}^{N-1} \sum_{v=0}^{N-1}F(u, v)cos(\frac{2x+1}{2N}u\pi)cos(\frac{2y+1}{2N}v\pi)\ \ \ \ x,y,u,v=0,1,…,N-1 \\ c(u)=c(v)=\begin{cases} \frac{1}{\sqrt{2}}\ \ u=0,v=0\\ 1 \ \ 其他 \end{cases} f(x,y)=N2u=0∑N−1v=0∑N−1F(u,v)cos(2N2x+1uπ)cos(2N2y+1vπ) x,y,u,v=0,1,...,N−1c(u)=c(v)={
21 u=0,v=01 其他
其中 F ( u , v ) F(u,v) F(u,v)为频域函数, f ( u , v ) f(u,v) f(u,v)为空域函数。
算法思路
水印嵌入算法
下列为 m × n m\times n m×n的灰度图原始载体图像和 k × h k\times h k×h的二值水印图像的水印嵌入过程。
- 将水印图像n次置乱处理得到置乱后的水印 矩阵 W 0 W_0 W0.
- 将 载 体 图 像分 为 k × h k\times h k×h个 子 块 ,对 每 个 子 块 做 DCT 变换,得到每个子块的DCT系数矩阵 C { i , j } C\{i,j\} C{
i,j}, i 、 j i、j i、j 表示第i行第j列的子块, 1 ≤ i ≤ m , 1 ≤ j ≤ n 1≤i≤m,1≤j≤n 1≤i≤m,1≤j≤n. - 对每个子块 C { i , j } C\{i,j\} C{
i,j}做奇异值分解 C { i , j } = U S V T C\{i,j\}=USV^T C{
i,j}=USVT, 得到 U , S , V U,S,V U,S,V. - 取一常数 q q q作为嵌入系数,将 S S S中的第一项 S ( 1 , 1 ) S(1,1) S(1,1)与 q q q相除得到的余数为 z z z。若 W 0 ( i , j ) W_0(i,j) W0(i,j)的值为1,则将 S ( 1 , 1 ) S(1,1) S(1,1)修改成 S ( 1 , 1 ) − z + q S(1,1)-z+q S(1,1)−z+q;若 W 0 ( i , j ) W_0(i,j) W0(i,j)值 为0,则 S ( 1 , 1 ) S(1,1) S(1,1)变为 S ( 1 , 1 ) − z + 0.5 q S(1,1)-z+0.5q S(1,1)−z+0.5q.
- 用水印信息修改后 S ′ S^′ S′构造新的矩阵 C { i , j } = U S ′ V T C\{i,j\}=US^′V^T C{
i,j}=US′VT. - 将每个新修改的 C { i , j } C\{i,j\} C{
i,j}分别做DCT逆变换,再合并为一个整图,即得到嵌入水印的新图像。
水印提取算法
- 将嵌入水印的图像分成 k × h k\times h k×h个子块并对每个子块做DTC变换,得到每个子块DCT系数 C ′ ′ { i , j } C^{”}\{i,j\} C′′{
i,j}, 1 ≤ i ≤ m , 1 ≤ j ≤ n 1≤i≤m,1≤j≤n 1≤i≤m,1≤j≤n; - 对每个子块 C i ′ ′ Ci^{′′} Ci′′进行奇异值分解, C ′ ′ { i , j } = U ′ ′ S ′ ′ V ′ ′ T C^{”}\{i,j\}=U^{′′}S^{′′}V^{′′T} C′′{
i,j}=U′′S′′V′′T,得到 S ′ ′ S^{′′} S′′. - 比较 S ′ ′ ( 1 , 1 ) S^{′′}(1,1) S′′(1,1)与嵌入系数q的大小,若比0大,则提取水印矩阵 W 0 ′ = 0 W_0^′=0 W0′=0,否则 W 0 ′ = 1 W_0^′=1 W0′=1.
- 对提取的 W 0 ′ W_0^′ W0′进行反置乱,即得到提取出的水印图像。
代码实现
下面代码的重要前提条件是:载体图像的长宽能被水印图像的长宽整除,否则就会出现bug。
clear;
img = imread("Always like this.png");
watermark = double(imread('watermark.png'));
img_grayed = double(rgb2gray(img));
key = 10; % key是对watermark进行Arnold置乱的次数
a = 1;b = 1;
[prow, pcol] = size(img_grayed);
[wrow, wcol] = size(watermark);
% 进行arnold置乱
watermark_arnolded = zeros(wrow, wcol);
for i = 1:key
for y = 1:wrow
for x = 1:wcol
xx = mod((x-1)+b*(y-1), wrow)+1;
yy = mod(a*(x-1)+(a*b+1)*(y-1), wrow)+1;
watermark_arnolded(yy, xx) = watermark(y, x);
end
end
watermark = watermark_arnolded;
end
%% 嵌入水印
img_block = mat2cell(img_grayed, (prow/wrow)*ones(1, wrow), (pcol/wcol)*ones(1, wcol));
q = 0.5;
img_res = zeros(prow, pcol);
for i = 1:wrow
for j = 1:wcol
temp_matrix = dct2(cell2mat(img_block(i, j)));
[U, S, V] = svd(temp_matrix);
z = rem(S(1, 1), q);
if watermark_arnolded(i, j) == 1
S(1, 1) = S(1, 1)-z+q;
elseif watermark_arnolded(i, j) == 0
S(1, 1) = S(1, 1)-z+0.5*q;
end
temp_matrix = U*S*V';
temp_matrix = idct2(temp_matrix);
for k = 1:(prow/wrow)
for h = 1:(pcol/wcol)
img_res((i-1)*(prow/wrow)+k, (j-1)*(pcol/wcol)+h) = temp_matrix(k, h);
end
end
end
end
subplot(1, 3, 1);
imshow(uint8(img_res));
title('加入水印后的图像') ;
%% 对水印进行提取
img_block = mat2cell(img_res, (prow/wrow)*ones(1, wrow), (pcol/wcol)*ones(1, wcol));
watermark_recovery = zeros(wrow, wcol);
for i = 1:wrow
for j=1:wcol
temp_matrix = cell2mat(img_block(i, j));
temp_matrix = dct2(temp_matrix);
[U, S, V] = svd(temp_matrix);
if rem(S(1, 1), q) > 0
watermark_recovery(i, j) = 0;
else
watermark_recovery(i, j) = 1;
end
end
end
subplot(1, 3, 2);
imshow(watermark_recovery);
title('提取出的水印图像');
%% 对水印反置乱
a = 1;b = 1;
key = 10;
watermark_res = zeros(wrow, wcol);
for i = 1:key
for y = 1:wrow
for x = 1:wcol
xx=mod((a*b+1)*(x-1)-b*(y-1), wrow)+1;
yy=mod(-a*(x-1)+(y-1), wrow)+1;
watermark_res(yy, xx) = watermark_recovery(y, x);
end
end
watermark_recovery = watermark_res;
end
figure(3);
imshow(watermark_res);
title('反置乱之后的水印图像');
运行结果
可以看到反置乱之后的水印充满各种噪点,经过python.cv2简单降噪之后手机仍然无法识别二维码,噪点出现的原因暂时不知道。(以后可能会解决?)
参考文献
[1]刘瑞祯,谭铁牛.基于奇异值分解的数字图像水印方法[J].电子学报,2001(02):168-171.
[2]丁珊,张定会,周雄葵.一种基于离散余弦变化和奇异值分解的数字水印算法[J].数据通信,2015(04):51-54.
今天的文章DiffIR图像复原_DiffIR图像复原「建议收藏」分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/62562.html