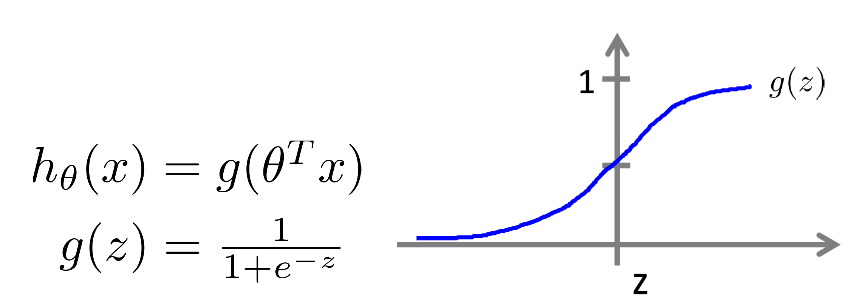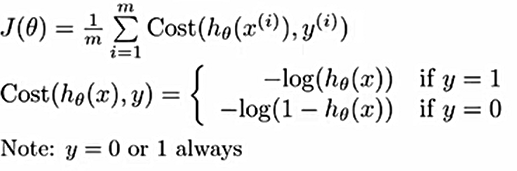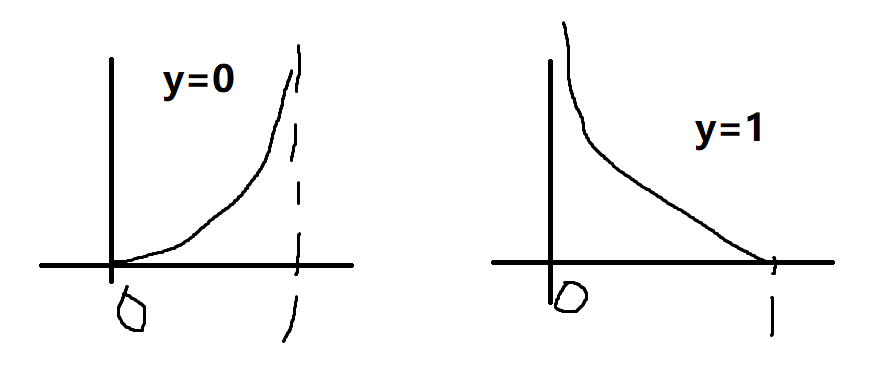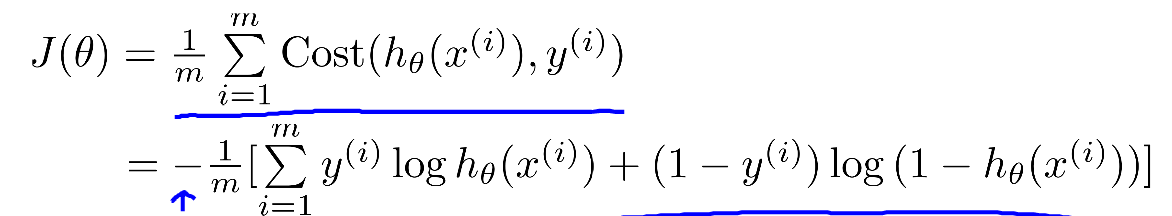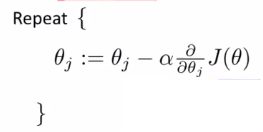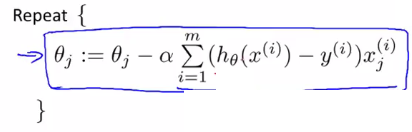机器学习（3）–LR算法

吴恩达ML课程课后总结，以供复习、总结、温故知新，也欢迎诸位评论讨论分享，一起探讨一起进步：

上一篇：机器学习（2）–单元、多元线性回归Python实现（附练习数据资源百度云）https://blog.csdn.net/qq_36187544/article/details/87888615

下一篇：机器学习（3）–正则化及python源码（附练习数据资源文件百度云）https://blog.csdn.net/qq_36187544/article/details/88060700

logistic regression 逻辑回归算法（LR）是一种分类算法

对于典型的分类问题，比如是否患病，今天天气是晴、下雨或是下雪等，对应的是一种离散型输出，就不适合用回归算法（回归算法可得到连续型输出）

通过LR构造分类器，带入数据可得到是趋于0还是趋于1，可返回[0,1]区间的概率范围，得到分类结果

LR怎么来的呢？来源于logistic function如下，该函数模型始终位于0，1之间，我们认为，当θTx>0时，即g(z)>0.5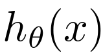（>0.5)，认为为1，否则为0。如果1和0对应是两种类别，则实现了分类

我们需要确定的是,其有可能是线性，有可能是非线性，比如或者

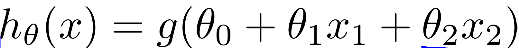
若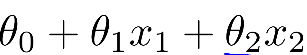>0，预测y=1等

确定了logistic function的形态，现在就是要确定θTx作为分类器的参数，确定了参数才确定了决策边界，决策边界通过设置不同的函数使边界形状不同，更为贴切数据，但是决策边界是假设本身及其参数的属性而不是数据集的属性（下图的决策边界为粉红色，×和⚪代表两种不同类型的数据）

同样，采取代价函数的方法来确定。

在线性回归中，代价函数是平方代价函数，是凸函数，具有良好的性态，但对于这个g(z)，是非凸函数，需要更改代价函数：

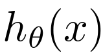
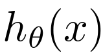
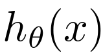
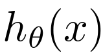
代价函数对应图像如其右，横坐标是logistic function的值，纵坐标是代价函数，目的仍旧是寻找代价函数最小值从而得到分类器的参数，个人理解：当y=0时即事件0发生，当===0时认为该θTx参数下的分类器完美匹配事件0，如果此时预测错误则代价会随之趋于无穷，同理，y=1时，===1认为此时分类器完美匹配事件1。（结合的概念意义）

代价函数的另一种综合写法：

现在就是求代价函数最小，仍旧是梯度下降法：

求偏导,该公式与线性回归梯度下降公式一模一样，只是在具体计算时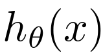是不一样得:

较梯度下降法更优的算法：conjugate gradient（共轭梯度）、BFGS、L-BFGS，不需要手动确定学习率，收敛更快，但是更复杂，建议不要自己写，因为设计高级数值计算

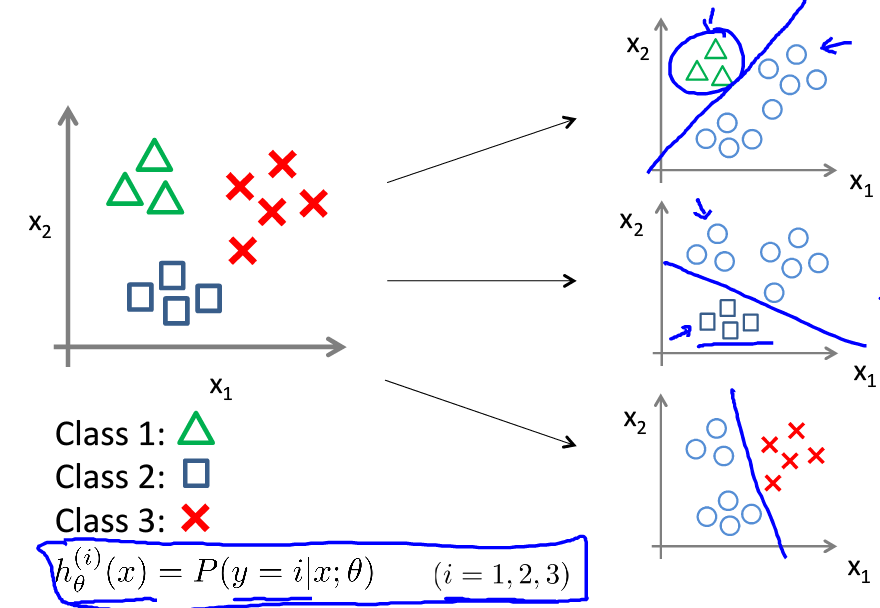
对于多类别分类，下图为两特征分3类：

对class1分类时，默认其他两类相同，计算代价函数,得到logistic function,最后进行分类判断时，分别带入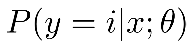求概率最大时对应得分类。

今天的文章机器学习（3）–LR算法分享到此就结束了，感谢您的阅读。