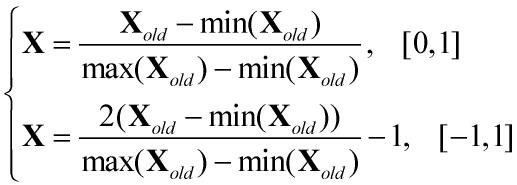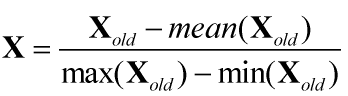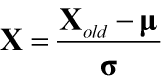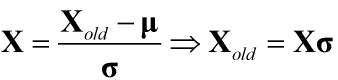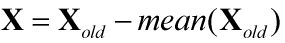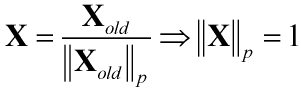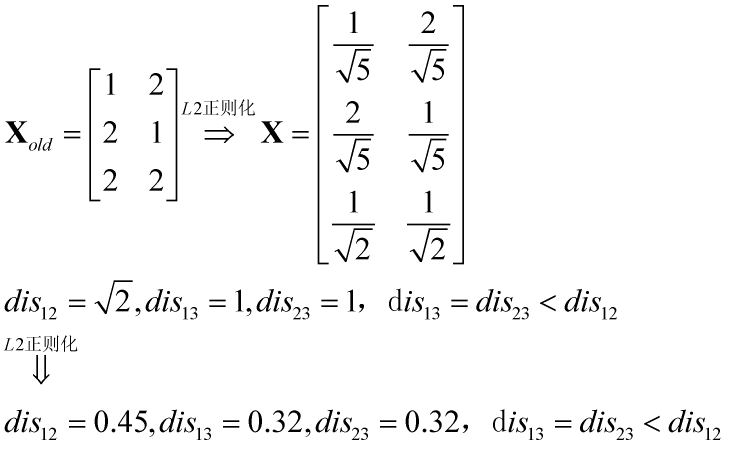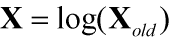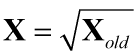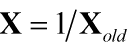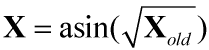机器学习之为什么要数据预处理？如何预处理数据？

在现实生活问题中，我们得到的原始数据往往非常混乱、不全面，机器学习模型往往无法从中有效识别并提取信息。数据和特征决定了机器学习的上限，而模型和算法只是逼近这个上限而已，在采集完数据后，机器学习建模的首要步骤以及主要步骤便是数据预处理。

真实的训练数据总是存在各种各样的问题：

各特征(变量)的尺度(量纲)和数量级差异大

存在噪声：包含错误和异常值

存在缺失值

存在冗余特征(变量)

…..

存在上述问题的数据有时也称为“脏数据”，这些”脏数据”会影响机器学习模型预测的有效性(有时会得到相反的结论)、可重复性和泛化能力，从而影响模型的质量。

例如：

数据预处理包含哪些处理？

特征缩放：数据标准化处理

缺失值处理

离群值/异常值处理

数据转换：数据类型转换和数据分布转换

数据缩减：降维

数据升维：多项式特征

数据预处理一般步骤：

1、数据清洗：

处理缺失值

识别错误分类

检测、处理异常值

标志变量？

将分类变量(非数值)转换为数值变量

绑定数值变量？

添加索引字段

删除无用变量

寻找有价值变量

2、数据集成：

组合/汇总来自多个资源的数据

删除重复记录

3、数据分布转换：

4、数据缩减：

降维

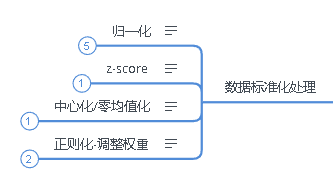
1.特征缩放：数据标准化处理

若原始数据中各维数据特征分布范围差异大，如果直接使用原始数据来建模，会突出数值尺度较大的特征在建模中的作用，而相对削弱或忽略数值尺度较小的特征的作用。因此，为了保证模型的有效性、可靠性，需要对原始数据的特征做特征缩放，使得各维特征对目标函数有相同权重的影响。

通常为了能够消除数据不同特征的尺度差异大的影响，需要把各维特征都缩放到同一个标准时，这样才具有可比性，这个过程就是数据标准化处理。

数据标准化处理

目标：使各维特征的取值均在相同的范围内以去除不同尺度特征的干扰。
作用：加快训练速度以及避免模型被分布范围较大或较小的特征干扰

1.1数据标准化处理包含哪些方法？

1.1.1.归一化

归一化主要有以下两种目标：

将数据各维特征映射到指定的范围之内：[0, 1]或者[-1, 1]
压缩量纲

就是将数据各维特征映射到指定的范围之内(通常映射到[0, 1]或者[-1, 1]之间)或者。

归一化类型可分为

极大极小归一化
均值归一化
非线性归一化

1）极大极小归一化公式如下所示

式中， $\mathbf{X}_{old}$ 为原始数据集，有m个样本，n项特征。 $min(\textbf{X}_{old})$ 、 $max(\textbf{X}_{old})$ 表示对原始数据集的各列特征分别取极值。

2）均值归一化公式如下所示

式中， $mean(\textbf{X}_{old})$ 表示对原始数据集的各列特征分别取均值。

3）非线性归一化指对原数据取对数。

非线性归一化没有把原数据各维特征缩放到某一范围内而是缩小各维特征的尺度(量纲)。平时在一些数据处理中，经常会把原始数据取对数后在做进一步处理。之所以这样做是基于对数函数在其定义域内是单调增函数，取对数之后不会改变数据的性质和相关关系，还可以压缩特征的尺度(量纲)。

归一化总结

特点：归一化会改变原始数据的数据分布，所以不能保留原始信息
对不同特征做伸缩变换，其目的是使得各个特征维度对目标函数的影响权重是同等程度的。同时，由于对不同特征做伸缩变换程度不同，使得那些扁平分布的目标函数的投影等高线趋于圆形，这样也就改变了原始数据的分布类型。
作用：
1、加快训练速度：如迭代算法中目标函数的收敛速度
2、平衡各维特征权重，避免数值尺度过大、过小的特征对模型的干扰
缺陷：
归一化处理数据后，虽然平衡了各维特征权重，但也改变了原始数据的数据分布，即破坏了数据结构。

1.1.2.z-score

z-score对数据标准化处理就是将数据缩放到以0为中心，标准差为1的某种数据分布(注意：均值为0，标准差为1的数据分布不一定是正态分布，也有可能是t分布或者其他分布)，此外，z-score保留原始数据信息，不会改变原数据分布类型。z-score的目的也是使原始数据的不同特征具有可比性。

z-score公式如下所示

式中， $\mu$ 为原始数据集的各列特征的均值的向量， $\mu$ = $mean(\textbf{X}_{old})$ ， $\sigma$ 为原始数据集的各列特征的标准差的向量。z-score的一个应用是测量原始数据与数据总体均值相差多少个标准差，如下所示

1.1.3归一化和z-score区别和联系

联系：

都是对原始数据做线性变换，即都是将样本点平移然后缩短距离，使原始数据的不同特征具有可比性。

区别：

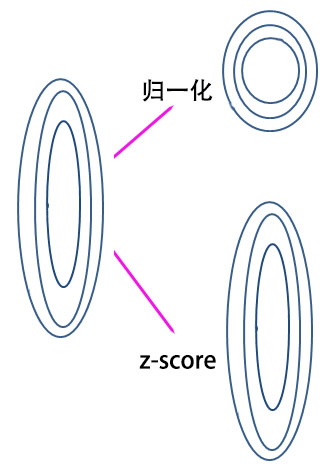
归一化对目标函数的影响体现在数值上，而z-score对目标函数的影响体现在数据几何分布上
归一化改变了数据的量级并同时也改变了数据的分布，Z-score只改变了数据的量级但未改变数据的分布类型。
标准化处理数据，不会改变目标函数的等高线投影，并且会继续保持原有目标函数扁平性，而归一化处理数据会使目标函数的等高线投影呈现圆形。
在梯度下降算法中，归一化处理数据有助于加快算法收敛速度。

图片来自知乎：https://zhuanlan.zhihu.com/p/?ivk_sa=u

为什么归一化改变了数据分布类型，而z-score没有改变？

归一化和标准化，都是将样本点平移然后缩短距离，不同的是，由于缩短尺度不同，要从公式方面理解，二者的主要不同是分母的缩短尺度不同，一个是极值差，另一个平均差(标准差)。

对于归一化方式处理的数据，它的每一项特征缩放程度都不同(因为每一项特征的极值可能都不同从而使每一项特征的缩放程度差异大)，而z-score处理的数据，它的每一项特征的缩放程度大体相同，因为除的都是平均值，效果是”温和的”、平稳的。所以归一化会改变数据分布(样本点的相对距离关系会被改变)，而z-socre不会使样本点之间的相对距离关系有根本变化。注意，这里样本点的关系用相对距离来表示。

举个例子，在SVM模型中，设(0,0)处有一个负例，(1,1)和(2,0.5)处各有一个正例。容易验证，取(0,0)和(1,1)为支持向量时，间隔最大。现在归一化处理数据，把水平方向缩小至原来的1/10，垂直方向缩小至原来的1/1(即两个维度的特征缩放程度差异大)，两个正例变成了(0.1,1)和(0.2,0.5)。容易验证，现在要让margin最大，支持向量就得取(0,0)和(0.2,0.5)了。你看，是不是改变了样本点的相对距离关系，从而也就改变了分布。

何时使用归一化或z-score预处理数据？

数据中各维特征尺度差异大(量纲)，目标函数易受尺度大的特征的干扰。比如涉及距离计算的模型：knn、kmeans、dbscan、svm等需要将数据量纲统一标准
使用梯度下降的参数估计模型：使用归一化处理后的数据可以提高算法收敛速度
涉及皮尔逊相关系数的模型：使用标准化处理的数据可以及方便计算相似度，why?
见文章相似性度量方法：相关系数和相似系数
PCA降维算法需要去中心化，可以使用z-score处理
对数值范围有具体要求的，需使用归一化处理数据，比如图像处理，其中像素强度必须归一化以适应一定范围(RGB颜色范围为0到255)
概率模型对特征量纲差异性不敏感，可以不做。如决策树
一般：不确定使用哪种数据处理方式时，就用z-score处理，至少z-score处理不会改变数据分布类型，即不会破坏数据结构。

1.2.中心化/零均值化

中心化处理后的数据，数据均值为0向量，就是将原始数据平移到原点附近。中心化处理数据就一个一个平移的过程，不会改变数据分布类型。中心化预处理表达式如下

作用：

方便计算协方差矩阵
去除截距项(偏置项)的影响
“增加基向量的正交性”？？？摘自网络，不理解

适用于PCA降维算法。见文章

1.3.正则化

正则化处理数据将每个样本的某个范数(L1范数、L2范数)缩放为1，即对每个样本计算其p-范数，然后对该样本中的每个元素除以该范数，使得处理后数据的每个样本的p-范数等于1。公式如下所示

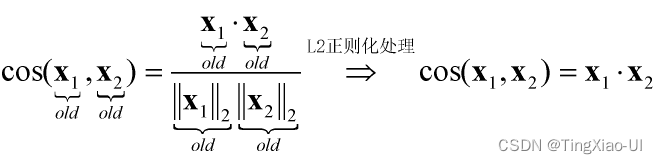
正则化处理数据主要应用于文本分类和聚类中，对需要计算样本间相似度有很大的作用，例如计算样本x1和样本x2的余弦相似度

正则化处理数据是否会改变数据分布类型？实践出真知，如下所示

貌似并不会改变数据分布类型，待严谨的数据证明……

1.4.哪些模型对标准化处理比较敏感？

基于距离度量的模型、决策边界学习模型：KNN、kmeans聚类、感知机和SVM
1、由于距离对特征之间不同取值范围非常敏感，若某个特征取值非常大而导致其掩盖了特征之间的距离对总距离的影响，这样距离模型便不能很好地将不同类别的特征区分开。所以基于距离读量的模型是十分有必要做数据预处理的，此类模型在标准化处理后可有可能提高精度。

2、有些模型在各个维度进行不均匀伸缩后，最优解与原来不等价，例如SVM。对于这样的模型，除非本来各维数据的分布范围就比较接近，否则必须进行z-score，以免模型参数被分布范围较大或较小的数据占住主导地位。
判别模型：指模型直接学习后验分布来进行分类，如逻辑回归
有些模型在各个维度进行不均匀伸缩后，最优解与原来等价，例如逻辑回归。对于这样的模型，是否标准化处理数据理论上不会改变最优解。但是，由于实际求解往往使用迭代算法，如果目标函数的形状太”扁”，迭代算法可能收敛得很慢甚至不收敛。所以对于具有伸缩不变性的模型，最好也进行标准化处理处理数据。
通过迭代优化算法求解最优解的模型：如逻辑回归模型
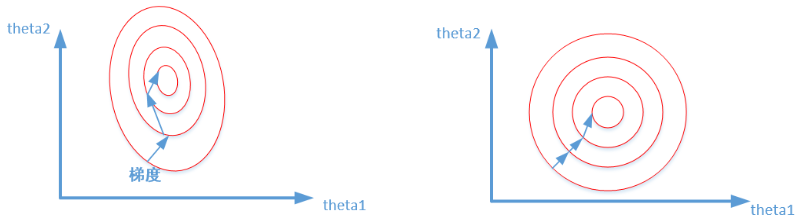
使用归一化来标准化处理数据可以加快迭代优化算法求最优解的速度，如运用梯度下降，其损失函数的等高线是椭圆形，需要进行多次迭代才能达到最优点，如果进行归一化了，那么等高线就是圆形的，促使往原点迭代，从而导致需要迭代次数较少。因此如果机器学习模型使用梯度下降法求最优解时，归一化往往非常有必要，否则很难收敛甚至不能收敛。

概率模型：如决策树、基于决策树的Boosting和Bagging等集成学习模型、随机森林
树模型是通过寻找最优分裂点构成的，样本点的特征缩放不影响分裂点的位置，对树模型的结构也不造成影响，而且树模型不能进行梯度下降，因为树模型是阶跃的，阶跃是不可导的，因此不需要归一化。
决策树、基于决策树的Boosting和Bagging等集成学习模型对于特征取值大小并不敏感。因为它们不关心变量的值，而是关心变量的分布和变量之间的条件概率。

1.5.什么情况下需要对数据标准化处理？

判断模型是否具有伸缩不变性以及模型算法是否使用了迭代优化算法？

一般概率模型具备伸缩不变性，因为对特征缩放处理不会对概率模型的结构造成影响，所以概率模型不必采用数据标准化处理，如决策树；但是，若概率模型计算目标函数过程中使用了迭代优化算法，为了能够加快算法收敛速度，可以对数据做归一化的标准化处理。

那些模型伸缩可变？即数据标准化处理前后得到的最优解不一致的模型？

基于距离计算的模型：回归算法(除了逻辑回归)、SVM、kmeans、dbsecan、
需要基于距离计算相似度的模型：最小角回归(基于距离计算相似度)
待归纳

伸缩可变的模型需要标准化处理。

1.6.训练集做了标准化处理后，然后训练出模型，那么测试集或者新样本是否如何处理？

待补充

2.缺失值处理

现实生活中的数据往往是不全面的，很多样本的属性值会有缺失，例如某个人填写的个人信息不完整或者对个人隐私的保护政策导致建模时可能无法得到所需要的特征，尤其是在数据量较大时，这种缺失值的产生会对模型的性能造成很大的影响

2.1.删除缺失值

处理缺失值最简单也是最暴力的方法便是删除含有缺失值的样本或者特征。注：工业上数据非常重要，一般不推荐这样做。

2.2填充缺失值

方法：使用用哪一种方法没有硬性的要求，具体问题具体分析

缺失值替换为：平均值、中位数、众数
使用KNN算法填充：缺失样本点周围最近的k个样本的均值或最大值填充(使用前提是，数据不是连片缺失，否则缺失样本点周围的样本也有缺失值，那就用不成了)
加权平均值/期望替换缺失值：比较含缺失值的样本与其他样本之间的的相似度，计算其加权平均值=Σ(特征值i*相似度i)/sum(相似度)，过程和基于用户相似度的SVD推荐系统差不多。
……

3.离群值/异常值处理

3.1异常检测

3.1.1异常样本

3.1.2异常特征

3.2检测原则

3.3处理方法

4.多项式特征

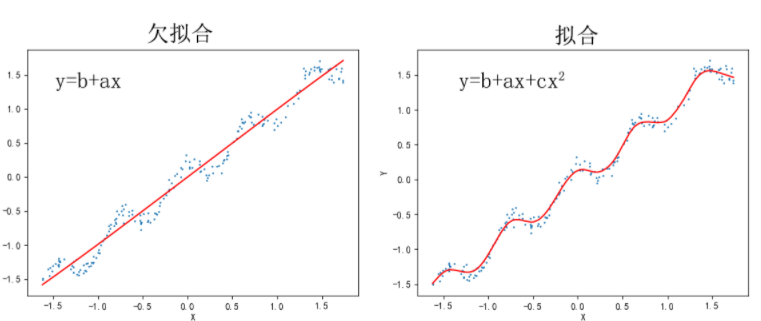
多项式特征是一种数据升维的方式，在线性回归中，当使用简单的x1,x2特征去拟合曲线，欠拟合，但是我们可以创建新的特征如 $x^{2}$ 去拟合数据，可能会得到一个较好的模型，所以我们有时候会对特征做一个多项式处理，即把特征 $x_{1},x_{2}$ 变成 $x_{1}^{2},x_{2}^{2}$ 。

5.数据转换

机器学习模型很多分布都采用高斯分布(正态分布)，如线性回归机器学习模型要求数据特征是高斯分布的。如果数据特征不是高斯分布，有时需要找到一个数学变换来把特征按照高斯分布进行变换。

5.1数据转换方法

数据转换为高斯分布方法：

对数变换
倒数变换
平方根变换
指数变换

以下总结摘自博客机器学习中的特征分布_TianCMCC的博客-CSDN博客_特征分布

对数变换：对于高度偏态（如Skewness为其标准误差的3倍以上）的数据分布，我们则可以对其取对数处理。其中又可分为自然对数和以10为基数的对数，其中以10为基数的对数处理纠偏力度最强，但有时会矫枉过正，将正偏态转换成负偏态。

平方根变换：平方根变换使服从泊松（Poisson）分布的样本或具有轻度偏态的样本正态化，或者是当各样本的方差与均数呈正相关时，使用平方根变换可使其达到方差齐性。

倒数变换：常用于分布两端波动较大的数据，倒数变换可使极端值的影响减小

平方根反正旋变换：常用于服从二项分布或百分比的数据。一般认为等总体率较小（如＜30%时）或较大（如＞70%时），偏离正态较为明显，通过样本率的平方根反正玄变换，可使数据接近正态分布，达到方差齐性的要求。

BOX-COX变换：通常用于连续的响应变量不满足正态分布的情况。在一些情况下（特征分布的P值<0.003）上述方法（平方变换等）很难实现正态化处理，所以可以考虑使用Box-Cox转换，但是当P值>0.003时，使用两种方法均可，优先考虑普通的平方变换。（其中 λ \lambdaλ 为待定变换参数）

注意：再次提醒Z – score标准化处理后的数据的特征并不一定遵循高斯分布。

为了使我们的数据趋向高斯分布，我们首先需要使数据对称，这意味着消除偏度，为了消除偏度，我们要对数据进行转换

实操演示：

待补充

5.1.1为什么机器学习中很多分布都采用高斯分布？

根据概率论中的中心极限定理，当样本容量无穷大时，许多分布的极限就是高斯分布(正态分布)现实中的很多随机变量是由大量相互独立的随机因素的综合影响所形成的，而其中每一个因素在总的影响中所起的作用都是微小的，这种随机变量往往近似服从高斯分布（中心极限定理的客观背景）。

熵：用来度量信息混乱程度

从熵的角度来看，在已知数据的均值和方差的情况下(原数据分布类型未知)，高斯分布的熵是所有其他分布中最大的。按照熵标准，“最大熵”约等价于“同约束下最接近均匀分布”，即更符合实际。可以这样理解，“熵最大”是为了使理想更接近实际，让特殊逼近一般，从而使模型更具一般性。注意高斯分布的熵其实是由方差决定的，“高斯变量最大熵”是在方差固定的背景下的结论。不同的方差显然会带来不同的高斯分布，而熵越大的高斯分布方差越大——在实轴上也越接近“均匀”

5.1.2是否一定要对数据转换分布

待补充

5.2 数据数值类型转换

针对非数值型数据，映射为数值。例如，现有一个汽车样本集，通过这个汽车样本集可以判断人们是否会购买该汽车。但是这个样本集的特征值是离散型的，为了确保计算机能正确读取该离散值的特征，需要给这些特征做编码处理，即创建一个映射表。如果特征值分类较少，可以选择自定义一个字典存放特征值与自定义值的关系。

5.2.1自定义数据类型编码

待补充

5.2.2独热编码

待补充

6.数据缩减

大数据集存在以下问题:

对一个模型来说，太多的预测特征会不必要地使分析的解释复杂化。
保留过多的特征可能会导致过度拟合。

解决这些问题最常用的方法之一是“降维”。此方法的目标是实现以下目标。

减少预测特征的数量。
确保这些预测项特征是独立的。

降维方法：

PCA
LDA
T-SNE

二、数据预处理实践

待补充

今天的文章
机器学习之为什么要数据预处理？如何预处理数据？分享到此就结束了，感谢您的阅读。

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容，请发送邮件至举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/89708.html