目录
(2)调整中心区棱块,使得每个中心区棱块都在正确的一面或者对立面
(3)调整中心区角块,使得每个中心区角块都在正确的一面或者对立面
齿轮魔方
1,魔方三要素
(1)组成部件
部件和三阶魔方完全对应,但每个棱块的朝向不止2种,而是有6种。
(2)可执行操作
只有3种操作,即上下层同时旋转180度、左右180度、前后180度。
但是旋转180度的这个操作,要重复12次才会回到最初的样子。
(3)目标态
所有块位置和朝向正确。
2,齿轮分析
当上下层同时旋转180度时,中间层旋转90度,且棱块自转300度。
为什么中间层和外层的公转比是1:2呢?因为外面2层是同时转的,按照对称性,自然是1:2。
为什么自转比公转是10:3呢?这个要看齿轮结构。
棱块有6个齿轮,它的轨道是每一面5个槽,即每公转90度就自转5/6*360=300度。
所以公转:自转 = 90:300 = 3:10
3,复原方法
(1)先复原所有块的位置,同时保证角块的朝向
很简单,不需要啥公式。
(2)调整棱块的方向
这一步也很简单,比如要调整中间层的4个棱块的朝向,只需要不停转动上下层,直到所有块回到原来位置,并且这4个棱块朝向也正确。
PS:齿轮魔方因为操作受限,不会出现各种复杂的场景。
五阶齿轮魔方
1,魔方三要素
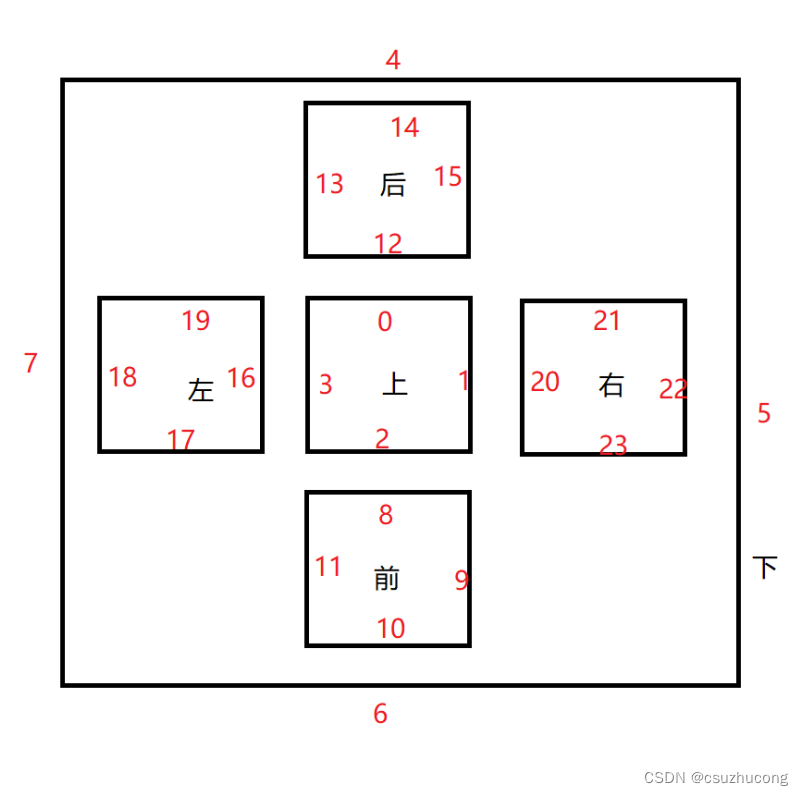
(1)组成部件
部件和五阶魔方完全对应。
图中圈出的3个红色小块是绑定起来的,对应五阶魔方的中心区棱块。
圈出的另外3个小块也是绑定起来的,对应五阶魔方的侧边区侧棱。
相比三阶齿轮魔方,五阶齿轮魔方和五阶魔方的对应更为接近,因为所有对应块的朝向数完全一样。
(2)可执行操作
有6种操作,即上下前后左右各顺时针旋转180度。
(3)目标态
所有块位置和朝向正确。
2,复原方法(V1)
(1)复原角块和侧边区中棱
先复原8个角块。
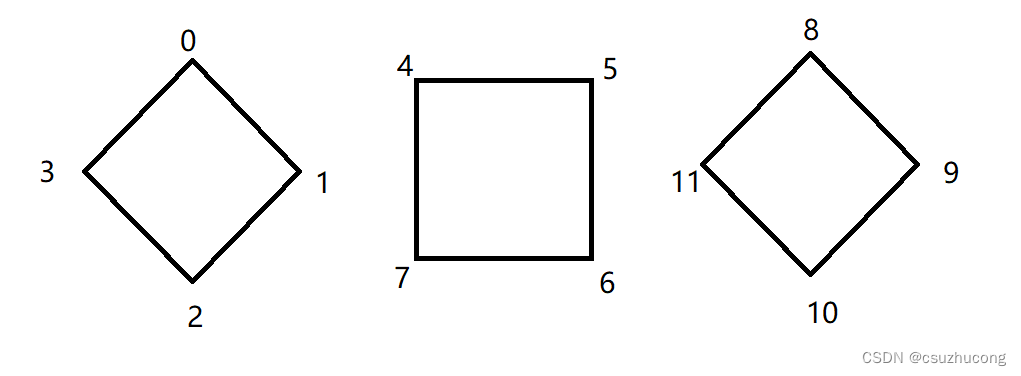
再把角块和侧边区中心棱按照交换公式自动推导中的默认编号进行编号,用那里面的代码,推导出3个公式:
0 1 2 3 5 4 7 6 8 9 10 11 0上 1下 2前 0上 1下 3后 效果是4567变成5476
0 3 2 1 4 5 7 6 8 9 10 11 0上 2前 0上 2前 0上 2前 效果是1367变成3176
0 1 2 3 7 5 4 6 8 9 10 11 0上 2前 0上 4左 0上 2前 0上 4左 效果是467变成746
有这3个公式,就可以搞定所有情况了。
(2)复原中心区棱块
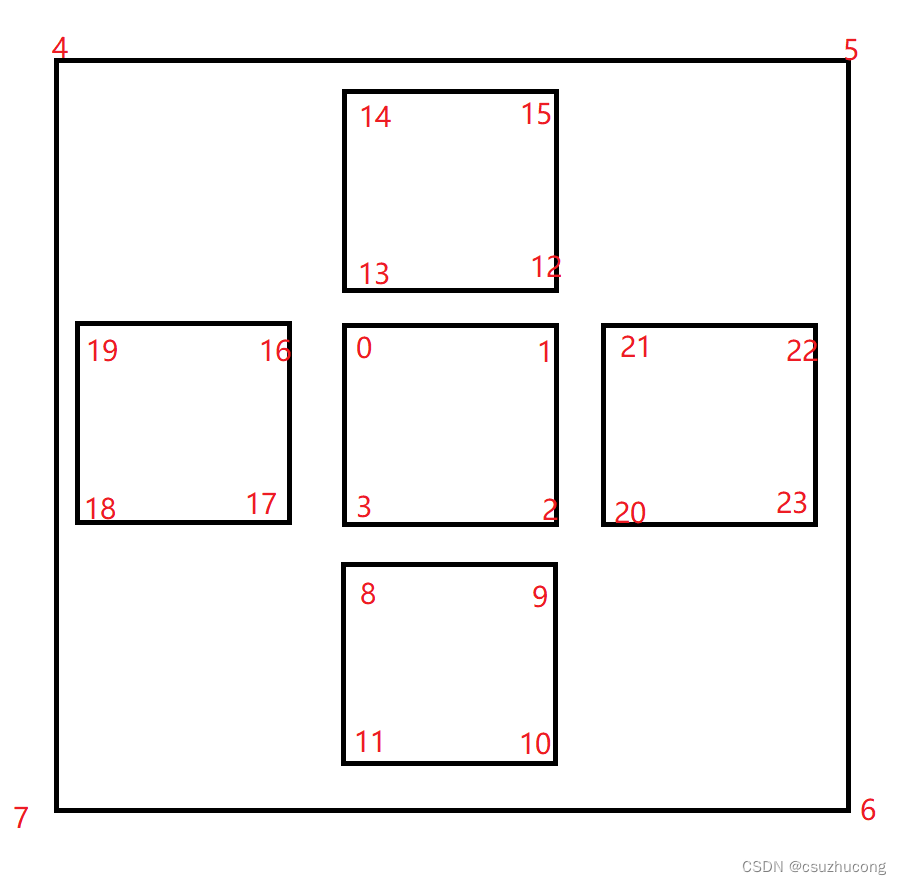
把24个中心区棱块编号:
int main() { CubeBlock block1(0, 8);//8角块 CubeBlock block2(1, 12);//12棱块 CubeBlock block3(2, 24);//24中心区棱块 vector<CubeBlock>b = vector<CubeBlock>{ block1,block2,block3 }; mans[0] = "上", mans[1] = "下", mans[2] = "前", mans[3] = "后", mans[4] = "左", mans[5] = "右"; vector<vector<int>>v1 = { {2,3,0,1,4,5,6,7},{2,3,0,1,4,5,6,7,8,9,10,11}, {2,3,0,1,4,5,6,7,20,9,10,11,16,13,14,15,8,17,18,19,12,21,22,23} }; vector<vector<int>>v2 = { {0,1,2,3,6,7,4,5},{0,1,2,3,4,5,6,7,10,11,8,9}, {0,1,2,3,6,7,4,5,8,9,18,11,12,13,22,15,16,17,14,19,20,21,10,23} }; vector<vector<int>>v3 = { {0,1,7,6,4,5,3,2},{0,1,10,3,4,5,7,6,8,9,2,11}, {0,1,17,3,4,5,23,7,10,11,8,9,12,13,14,15,16,6,18,19,20,21,22,2} }; vector<vector<int>>v4 = { {5,4,2,3,1,0,6,7},{8,1,2,3,5,4,6,7,0,9,10,11}, {21,1,2,3,19,5,6,7,8,9,10,11,14,15,12,13,16,17,18,0,20,4,22,23} }; vector<vector<int>>v5 = { {7,1,2,4,3,5,6,0},{0,1,2,11,7,5,6,4,8,9,10,3} , {0,1,2,13,4,5,6,11,8,9,10,3,12,7,14,15,18,19,16,17,20,21,22,23} }; vector<vector<int>>v6 = { {0,6,5,3,4,2,1,7},{0,9,2,3,4,6,5,7,8,1,10,11}, {0,9,2,3,4,15,6,7,8,5,10,11,12,13,14,1,16,17,18,19,22,23,20,21} }; CubeOpt op1(b, v1); CubeOpt op2(b, v2); CubeOpt op3(b, v3); CubeOpt op4(b, v4); CubeOpt op5(b, v5); CubeOpt op6(b, v6); vector<CubeOpt>opts = { op1,op2,op3,op4,op5,op6 }; Cube cube(b, opts); cube.bfs(2, 2, 4); return 0; }输出若干行,挑选出这2行:
6 1 0 3 4 5 2 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 0上 0上 0上 2前 2前 0上 2前 2前
0 1 2 3 4 5 6 7 8 9 16 11 12 13 14 15 20 17 18 19 10 21 22 23 0上 2前 0上 0上 2前 2前 2前 0上
有这2个公式,稍加思索组合,灵活运用,应该就可以搞定所有情况。
(3)复原中心区角块
把24个中心区角块编号:
int main() { CubeBlock block1(0, 8);//8角块 CubeBlock block2(1, 12);//12棱块 CubeBlock block3(2, 24);//24中心区棱块 CubeBlock block4(3, 24);//24中心区角块 vector<CubeBlock>b = vector<CubeBlock>{ block1,block2,block3,block4 }; mans[0] = "上", mans[1] = "下", mans[2] = "前", mans[3] = "后", mans[4] = "左", mans[5] = "右"; vector<vector<int>>v1 = { {2,3,0,1,4,5,6,7},{2,3,0,1,4,5,6,7,8,9,10,11}, {2,3,0,1,4,5,6,7,20,9,10,11,16,13,14,15,8,17,18,19,12,21,22,23}, {2,3,0,1,4,5,6,7,20,21,10,11,16,17,14,15,8,9,18,19,12,13,22,23} }; vector<vector<int>>v2 = { {0,1,2,3,6,7,4,5},{0,1,2,3,4,5,6,7,10,11,8,9}, {0,1,2,3,6,7,4,5,8,9,18,11,12,13,22,15,16,17,14,19,20,21,10,23}, {0,1,2,3,6,7,4,5,8,9,18,19,12,13,22,23,16,17,14,15,20,21,10,11} }; vector<vector<int>>v3 = { {0,1,7,6,4,5,3,2},{0,1,10,3,4,5,7,6,8,9,2,11}, {0,1,17,3,4,5,23,7,10,11,8,9,12,13,14,15,16,6,18,19,20,21,22,2}, {0,1,17,18,4,5,20,23,10,11,8,9,12,13,14,15,16,7,6,19,3,21,22,2} }; vector<vector<int>>v4 = { {5,4,2,3,1,0,6,7},{8,1,2,3,5,4,6,7,0,9,10,11}, {21,1,2,3,19,5,6,7,8,9,10,11,14,15,12,13,16,17,18,0,20,4,22,23}, {21,22,2,3,16,19,6,7,8,9,10,11,14,15,12,13,1,17,18,0,20,5,4,23} }; vector<vector<int>>v5 = { {7,1,2,4,3,5,6,0},{0,1,2,11,7,5,6,4,8,9,10,3} , {0,1,2,13,4,5,6,11,8,9,10,3,12,7,14,15,18,19,16,17,20,21,22,23}, {14,1,2,13,11,5,6,8,0,9,10,3,12,4,7,15,18,19,16,17,20,21,22,23} }; vector<vector<int>>v6 = { {0,6,5,3,4,2,1,7},{0,9,2,3,4,6,5,7,8,1,10,11}, {0,9,2,3,4,15,6,7,8,5,10,11,12,13,14,1,16,17,18,19,22,23,20,21}, {0,9,10,3,4,12,15,7,8,6,5,11,2,13,14,1,16,17,18,19,22,23,20,21} }; CubeOpt op1(b, v1); CubeOpt op2(b, v2); CubeOpt op3(b, v3); CubeOpt op4(b, v4); CubeOpt op5(b, v5); CubeOpt op6(b, v6); vector<CubeOpt>opts = { op1,op2,op3,op4,op5,op6 }; Cube cube(b, opts); cube.bfs(3, 2, 6); return 0; }程序计算能力有限,无法枚举所有情况,只得到2条公式:
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 20 19 18 21 22 17 16 23 0上 0上 3后 3后 0上 0上 3后 3后
0 1 2 3 4 5 6 7 22 13 10 11 8 19 14 15 16 17 18 9 20 21 12 23 0上 3后 3后 0上 0上 3后 3后 0上
这2个公式都是改变6个块的位置,用起来比较复杂。
于是我想到,或许先从中心区开始拼更合理。
int main() { CubeBlock block1(0, 24);//24中心区棱块 CubeBlock block2(1, 24);//24中心区角块 vector<CubeBlock>b = vector<CubeBlock>{ block1,block2 }; mans[0] = "上", mans[1] = "下", mans[2] = "前", mans[3] = "后", mans[4] = "左", mans[5] = "右"; vector<vector<int>>v1 = { {2,3,0,1,4,5,6,7,20,9,10,11,16,13,14,15,8,17,18,19,12,21,22,23}, {2,3,0,1,4,5,6,7,20,21,10,11,16,17,14,15,8,9,18,19,12,13,22,23} }; vector<vector<int>>v2 = { {0,1,2,3,6,7,4,5,8,9,18,11,12,13,22,15,16,17,14,19,20,21,10,23}, {0,1,2,3,6,7,4,5,8,9,18,19,12,13,22,23,16,17,14,15,20,21,10,11} }; vector<vector<int>>v3 = { {0,1,17,3,4,5,23,7,10,11,8,9,12,13,14,15,16,6,18,19,20,21,22,2}, {0,1,17,18,4,5,20,23,10,11,8,9,12,13,14,15,16,7,6,19,3,21,22,2} }; vector<vector<int>>v4 = { {21,1,2,3,19,5,6,7,8,9,10,11,14,15,12,13,16,17,18,0,20,4,22,23}, {21,22,2,3,16,19,6,7,8,9,10,11,14,15,12,13,1,17,18,0,20,5,4,23} }; vector<vector<int>>v5 = { {0,1,2,13,4,5,6,11,8,9,10,3,12,7,14,15,18,19,16,17,20,21,22,23}, {14,1,2,13,11,5,6,8,0,9,10,3,12,4,7,15,18,19,16,17,20,21,22,23} }; vector<vector<int>>v6 = { {0,9,2,3,4,15,6,7,8,5,10,11,12,13,14,1,16,17,18,19,22,23,20,21}, {0,9,10,3,4,12,15,7,8,6,5,11,2,13,14,1,16,17,18,19,22,23,20,21} }; CubeOpt op1(b, v1); CubeOpt op2(b, v2); CubeOpt op3(b, v3); CubeOpt op4(b, v4); CubeOpt op5(b, v5); CubeOpt op6(b, v6); vector<CubeOpt>opts = { op1,op2,op3,op4,op5,op6 }; Cube cube(b, opts); cube.bfs(1, 1, 4); return 0; }运行得不到结果。
或者反过来:cube.bfs(0, 1, 4);
还是得不到结果。
也就是说,即使只看中心区,也得不到很简洁的公式,说明当前代码能力有限。
一个很显然的限制就是,没有考虑中心区的块之间是有对称性的,即24个块其实只有6种颜色。
修改代码:
int changeNum() { int ans = 0; for (int i = 0; i < v.size(); i++) { if (v.size() == 24) { if (v[i] / 4 != i / 4)ans++; } else { if (v[i] != i)ans++; } } return ans; }运行结果依然不变。
于是我再加上开放式尝试:(注意修改代码中的mans)
int main() { CubeBlock block1(0, 24);//24中心区棱块 CubeBlock block2(1, 24);//24中心区角块 vector<CubeBlock>b = vector<CubeBlock>{ block1,block2 }; vector<vector<int>>v1 = { {2,3,0,1,4,5,6,7,20,9,10,11,16,13,14,15,8,17,18,19,12,21,22,23}, {2,3,0,1,4,5,6,7,20,21,10,11,16,17,14,15,8,9,18,19,12,13,22,23} }; vector<vector<int>>v2 = { {0,1,2,3,6,7,4,5,8,9,18,11,12,13,22,15,16,17,14,19,20,21,10,23}, {0,1,2,3,6,7,4,5,8,9,18,19,12,13,22,23,16,17,14,15,20,21,10,11} }; vector<vector<int>>v3 = { {0,1,17,3,4,5,23,7,10,11,8,9,12,13,14,15,16,6,18,19,20,21,22,2}, {0,1,17,18,4,5,20,23,10,11,8,9,12,13,14,15,16,7,6,19,3,21,22,2} }; vector<vector<int>>v4 = { {21,1,2,3,19,5,6,7,8,9,10,11,14,15,12,13,16,17,18,0,20,4,22,23}, {21,22,2,3,16,19,6,7,8,9,10,11,14,15,12,13,1,17,18,0,20,5,4,23} }; vector<vector<int>>v5 = { {0,1,2,13,4,5,6,11,8,9,10,3,12,7,14,15,18,19,16,17,20,21,22,23}, {14,1,2,13,11,5,6,8,0,9,10,3,12,4,7,15,18,19,16,17,20,21,22,23} }; vector<vector<int>>v6 = { {0,9,2,3,4,15,6,7,8,5,10,11,12,13,14,1,16,17,18,19,22,23,20,21}, {0,9,10,3,4,12,15,7,8,6,5,11,2,13,14,1,16,17,18,19,22,23,20,21} }; CubeOpt op1(b, v1); CubeOpt op2(b, v2); CubeOpt op3(b, v3); CubeOpt op4(b, v4); CubeOpt op5(b, v5); CubeOpt op6(b, v6); vector<CubeOpt>opts = { op1,op3,op5}; mans[0] = "上", mans[1] = "前", mans[2] = "左"; Cube cube(b, opts); cube.bfs(1, 1, 4); return 0; }选出这几行:
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 18 21 20 19 16 23 22 17 0上 0上 1前 1前 0上 0上 1前 1前(16 17和20 21交换)
2 1 0 9 6 5 4 12 8 3 10 11 7 13 14 15 16 17 18 19 20 21 22 23 2左 0上 0上 2左 1前 1前 2左 0上 0上 2左 1前 1前(3 9交换,7 12交换)
0 1 8 3 4 5 13 7 2 11 10 9 14 6 12 15 16 17 18 19 20 21 22 23 0上 0上 2左 1前 1前 2左 0上 0上 2左 1前 1前 2左(2 8交换,6 13交换)
2 6 7 3 1 5 4 0 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 0上 0上 0上 1前 1前 2左 2左 1前 1前 2左 2左 0上(01和67交换)
21 1 2 3 16 5 6 7 8 9 10 11 12 13 14 15 18 17 4 19 20 23 22 0 0上 0上 1前 2左 2左 1前 1前 2左 2左 1前 0上 0上(0 21交换 4 16交换)
因为这些公式都符合连连看规则,即相邻2个相同就消掉,最后就全消了,所以肯定也不会影响不在代码中的角块和侧边区中棱。
然而靠这5个公式去复原所有中心区角块实在有点难,于是我决定研究第二种思路。
(4)复原侧边区侧棱
略
3,复原方法(V2)
(1)复原角块和侧边区中棱
同V1
(2)调整中心区棱块,使得每个中心区棱块都在正确的一面或者对立面
比V1的复原中心区棱块简单一点。
(3)调整中心区角块,使得每个中心区角块都在正确的一面或者对立面
修改changeNum:
int changeNum() { int ans = 0; for (int i = 0; i < v.size(); i++) { if (v.size() == 24) { if (v[i] / 8 != i / 8)ans++; } else { if (v[i] != i)ans++; } } return ans; }这样才能跑出只影响2个块的公式:
int main() { CubeBlock block1(0, 24);//24中心区棱块 CubeBlock block2(1, 24);//24中心区角块 vector<CubeBlock>b = vector<CubeBlock>{ block1,block2 }; vector<vector<int>>v1 = { {2,3,0,1,4,5,6,7,20,9,10,11,16,13,14,15,8,17,18,19,12,21,22,23}, {2,3,0,1,4,5,6,7,20,21,10,11,16,17,14,15,8,9,18,19,12,13,22,23} }; vector<vector<int>>v2 = { {0,1,2,3,6,7,4,5,8,9,18,11,12,13,22,15,16,17,14,19,20,21,10,23}, {0,1,2,3,6,7,4,5,8,9,18,19,12,13,22,23,16,17,14,15,20,21,10,11} }; vector<vector<int>>v3 = { {0,1,17,3,4,5,23,7,10,11,8,9,12,13,14,15,16,6,18,19,20,21,22,2}, {0,1,17,18,4,5,20,23,10,11,8,9,12,13,14,15,16,7,6,19,3,21,22,2} }; vector<vector<int>>v4 = { {21,1,2,3,19,5,6,7,8,9,10,11,14,15,12,13,16,17,18,0,20,4,22,23}, {21,22,2,3,16,19,6,7,8,9,10,11,14,15,12,13,1,17,18,0,20,5,4,23} }; vector<vector<int>>v5 = { {0,1,2,13,4,5,6,11,8,9,10,3,12,7,14,15,18,19,16,17,20,21,22,23}, {14,1,2,13,11,5,6,8,0,9,10,3,12,4,7,15,18,19,16,17,20,21,22,23} }; vector<vector<int>>v6 = { {0,9,2,3,4,15,6,7,8,5,10,11,12,13,14,1,16,17,18,19,22,23,20,21}, {0,9,10,3,4,12,15,7,8,6,5,11,2,13,14,1,16,17,18,19,22,23,20,21} }; CubeOpt op1(b, v1); CubeOpt op2(b, v2); CubeOpt op3(b, v3); CubeOpt op4(b, v4); CubeOpt op5(b, v5); CubeOpt op6(b, v6); vector<CubeOpt>opts = { op1,op3,op5}; mans[0] = "上", mans[1] = "前", mans[2] = "左"; Cube cube(b, opts); cube.bfs(1, 1, 2); return 0; }输出若干行选出3行:
0 6 2 3 4 5 1 7 14 13 8 12 10 11 17 15 20 21 23 19 16 18 22 9 0上 1前 1前 0上 2左 1前 0上 0上 1前 1前 1前 2左 (9 17交换)
7 1 4 12 3 5 2 0 10 13 14 6 8 11 9 15 16 17 18 23 20 21 22 19 0上 1前 1前 1前 2左 2左 1前 0上 2左 1前 1前 2左 (6 12交换)
2 1 7 6 4 5 3 23 12 9 10 11 8 13 14 15 20 0 16 19 18 21 22 17 0上 1前 2左 2左 1前 1前 1前 0上 1前 2左 2左 1前 (0 23交换)
有了这3个公式稍加组合运用就可以了。
PS:
灵活运用的技巧有很多,比如要交换8和16,只需要把交换9和17的公式0做个镜面变换即可。
(4)复原中心区棱块
int changeNum() { int ans = 0; for (int i = 0; i < v.size(); i++) { if (v.size() == 24) { if (typeId == 1) { if (v[i] / 8 != i / 8)ans++; } else { if (v[i] / 4 != i / 4)ans++; } } else { if (v[i] != i)ans++; } } return ans; }搜索:
int main() { CubeBlock block1(0, 24);//24中心区棱块 CubeBlock block2(1, 24);//24中心区角块 vector<CubeBlock>b = vector<CubeBlock>{ block1,block2 }; vector<vector<int>>v1 = { {2,3,0,1,4,5,6,7,20,9,10,11,16,13,14,15,8,17,18,19,12,21,22,23}, {2,3,0,1,4,5,6,7,20,21,10,11,16,17,14,15,8,9,18,19,12,13,22,23} }; vector<vector<int>>v2 = { {0,1,2,3,6,7,4,5,8,9,18,11,12,13,22,15,16,17,14,19,20,21,10,23}, {0,1,2,3,6,7,4,5,8,9,18,19,12,13,22,23,16,17,14,15,20,21,10,11} }; vector<vector<int>>v3 = { {0,1,17,3,4,5,23,7,10,11,8,9,12,13,14,15,16,6,18,19,20,21,22,2}, {0,1,17,18,4,5,20,23,10,11,8,9,12,13,14,15,16,7,6,19,3,21,22,2} }; vector<vector<int>>v4 = { {21,1,2,3,19,5,6,7,8,9,10,11,14,15,12,13,16,17,18,0,20,4,22,23}, {21,22,2,3,16,19,6,7,8,9,10,11,14,15,12,13,1,17,18,0,20,5,4,23} }; vector<vector<int>>v5 = { {0,1,2,13,4,5,6,11,8,9,10,3,12,7,14,15,18,19,16,17,20,21,22,23}, {14,1,2,13,11,5,6,8,0,9,10,3,12,4,7,15,18,19,16,17,20,21,22,23} }; vector<vector<int>>v6 = { {0,9,2,3,4,15,6,7,8,5,10,11,12,13,14,1,16,17,18,19,22,23,20,21}, {0,9,10,3,4,12,15,7,8,6,5,11,2,13,14,1,16,17,18,19,22,23,20,21} }; CubeOpt op1(b, v1); CubeOpt op2(b, v2); CubeOpt op3(b, v3); CubeOpt op4(b, v4); CubeOpt op5(b, v5); CubeOpt op6(b, v6); vector<CubeOpt>opts = { op1,op3,op5}; mans[0] = "上", mans[1] = "前", mans[2] = "左"; Cube cube(b, opts); cube.bfs(0, 1, 4); return 0; }得到公式:
6 3 0 7 4 5 2 1 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 0上 1前 1前 0上 1前 1前 2左 2左 0上 2左 2左 0上(12和67交换)
灵活运用即可。
(5)复原中心区角块
同V1。
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 18 21 20 19 16 23 22 17 0上 0上 1前 1前 0上 0上 1前 1前(16 17和20 21交换)
2 1 0 9 6 5 4 12 8 3 10 11 7 13 14 15 16 17 18 19 20 21 22 23 2左 0上 0上 2左 1前 1前 2左 0上 0上 2左 1前 1前(3 9交换,7 12交换)
0 1 8 3 4 5 13 7 2 11 10 9 14 6 12 15 16 17 18 19 20 21 22 23 0上 0上 2左 1前 1前 2左 0上 0上 2左 1前 1前 2左(2 8交换,6 13交换)
2 6 7 3 1 5 4 0 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 0上 0上 0上 1前 1前 2左 2左 1前 1前 2左 2左 0上(01和67交换)
21 1 2 3 16 5 6 7 8 9 10 11 12 13 14 15 18 17 4 19 20 23 22 0 0上 0上 1前 2左 2左 1前 1前 2左 2左 1前 0上 0上(0 21交换 4 16交换)
虽然情况变简单了一点,但是我发现后面还是很难!
于是我又用dp的思想,把已有的5个公式添加到基础操作集中,再加上开放式尝试,找出更强大的公式(唯一的缺点就是长了点)
int main() { CubeBlock block0(0, 24);//24中心区棱块 CubeBlock block1(1, 24);//24中心区角块 vector<CubeBlock>b = vector<CubeBlock>{ block0,block1 }; vector<vector<int>>v1 = { {0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23}, {0, 1 ,2, 3, 4,5 ,6,7 ,8, 9 ,10 ,11 ,12, 13 ,14, 15, 18, 21, 20, 19, 16, 23,22, 17 } }; vector<vector<int>>v5 = { {0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23}, {21, 1, 2, 3 ,16 ,5 ,6 ,7, 8, 9, 10, 11, 12 ,13 ,14 ,15, 18, 17 ,4, 19 ,20, 23 ,22, 0} }; vector<vector<int>>v6 = { {2,3,0,1,4,5,6,7,20,9,10,11,16,13,14,15,8,17,18,19,12,21,22,23}, {2, 3, 0, 1, 4, 5, 6, 7, 20, 21, 10, 11, 16, 17, 14, 15, 8, 9, 18, 19, 12, 13, 22, 23} }; vector<vector<int>>v7 = { {0,1,17,3,4,5,23,7,10,11,8,9,12,13,14,15,16,6,18,19,20,21,22,2}, {0,1,17,18,4,5,20,23,10,11,8,9,12,13,14,15,16,7,6,19,3,21,22,2} }; vector<vector<int>>v8 = { {0,1,2,13,4,5,6,11,8,9,10,3,12,7,14,15,18,19,16,17,20,21,22,23}, {14, 1, 2, 13, 11, 5, 6, 8, 0, 9, 10, 3, 12, 4, 7, 15, 18, 19, 16, 17, 20, 21, 22, 23} }; CubeOpt op1(b, v1); CubeOpt op5(b, v5); CubeOpt op6(b, v6); CubeOpt op7(b, v7); CubeOpt op8(b, v8); vector<CubeOpt>opts = { op1,op5,op6,op8}; mans[0] = "上 上 前 前 上 上 前 前"; mans[1] = "上 上 前 左 左 前 前 左 左 前 上 上"; mans[2] = "上", mans[3] = "左"; Cube cube(b, opts); cube.bfs(1, 1, 2); return 0; }输出内容中整理出这几个公式:
0 1 2 3 16 5 6 7 8 9 10 11 12 13 14 15 18 19 4 17 20 23 22 21 上 上 前 前 上 上 前 前 上 上 前 左左 前 前 左 左 前 上 上 左 上 上 前 前 上 上 前 前 左 左 左 上 上 前 左 左 前 前 左 左 前 前 前 上 上 前 前 (4 16交换)
21 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 19 18 17 20 0 22 23 上 上 前 前 上 上 前 前 上 上 前 左左 前 前 左 左 前 上 上 左 上 上 前 前 上 上 前 前左 上 上 前 前 上 上 前 前上 上 前 前 上 上 前 前 左 左 上 上 前 左 左 前 前 左 左 前 上 上 (0 21交换)
23 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 19 18 17 20 21 22 0 上 上 前 左 左 前 前 左 左 前 前 前 上 上 前 前上 上 前 前 上 上 前 前 左 上 上 前 前 上 上 前 前 左 左 左 上 上 前 左 左 前 前 左 左 前 前 前 上 上 前 前(0 23交换)
0 1 2 3 18 5 6 7 8 9 10 11 12 13 14 15 4 19 16 17 20 23 22 21 上 上 前 左 左 前 前 左 左 前 前 前 上 上 前 前左 上 上 前 前 上 上 前 前上 上 前 前 上 上 前 前左 上 上 前 前 上 上 前 前 左 左 上 上 前 左 左 前 前 左 左 前 上 上(4 18交换)
21 1 0 3 4 5 6 7 8 11 10 9 14 13 12 15 18 17 16 19 20 23 22 2 上 上 前 左 左 前 前 左 左 前 上 前 前 上 上 前 前 上 上 前 左 左 前 前 左 左 前 上 上上 左 左 上 上 左 左(2 21交换)
依法炮制,再用这些公式又可以继续生成公式:
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 21 18 17 20 19 22 23 上 上 前 前 上 上 前 前 上 上 前 前 上 上 前 前 上 上 前 左左 前 前 左 左 前 上 上 左 上 上 前 前 上 上 前 前 左 左 左 上 上 前 左 左 前 前 左 左 前 前 前 上 上 前 前 上 上 前 前 上 上 前 前 上 上 前 前 上 上 前 前 上 上 前 左左 前 前 左 左 前 上 上 左 上 上 前 前 上 上 前 前 左 左 左 上 上 前 左 左 前 前 左 左 前 前 前 上 上 前 前 (17和21交换)
0 1 2 3 4 5 6 7 8 9 10 18 12 13 14 15 11 19 16 17 20 23 22 21 左 上 上 前 前 上 上 前 前 上 上 前 左左 前 前 左 左 前 上 上 左 上 上 前 前 上 上 前 前 左 左 左 上 上 前 左 左 前 前 左 左 前 前 前 上 上 前 前 左 左 左(11和18交换)
至此,这一套公式终于比较好用了。
(6)调整侧边区侧棱位置
先试下基本代码:
int changeNum() { int ans = 0; for (int i = 0; i < v.size(); i++) { if (v.size() == 24) { if (typeId == 2) { if (v[i] != i)ans++; } else { if (v[i]/4 != i/4)ans++; } } else { if (v[i] != i)ans++; } } return ans; } int main() { CubeBlock block1(0, 24);//24中心区棱块 CubeBlock block2(1, 24);//24中心区角块 CubeBlock block3(2, 24);//24侧边区侧棱 vector<CubeBlock>b = vector<CubeBlock>{ block1,block2,block3 }; mans[0] = "上", mans[1] = "下", mans[2] = "前", mans[3] = "后", mans[4] = "左", mans[5] = "右"; vector<vector<int>>v1 = { {2,3,0,1,4,5,6,7,20,9,10,11,16,13,14,15,8,17,18,19,12,21,22,23}, {2,3,0,1,4,5,6,7,20,21,10,11,16,17,14,15,8,9,18,19,12,13,22,23}, {4,5,6,7,0,1,2,3,11,8,9,10,12,13,14,15,16,17,18,19,20,21,22,23} }; vector<vector<int>>v2 = { {0,1,2,3,6,7,4,5,8,9,18,11,12,13,22,15,16,17,14,19,20,21,10,23}, {0,1,2,3,6,7,4,5,8,9,18,19,12,13,22,23,16,17,14,15,20,21,10,11}, {0,1,2,3,4,5,6,7,8,9,10,11,13,14,15,12,20,21,22,23,16,17,18,19} }; vector<vector<int>>v3 = { {0,1,17,3,4,5,23,7,10,11,8,9,12,13,14,15,16,6,18,19,20,21,22,2}, {0,1,17,18,4,5,20,23,10,11,8,9,12,13,14,15,16,7,6,19,3,21,22,2}, {0,1,2,6,21,20,22,7,8,14,13,11,12,10,9,15,16,17,18,3,5,4,19,23} }; vector<vector<int>>v4 = { {21,1,2,3,19,5,6,7,8,9,10,11,14,15,12,13,16,17,18,0,20,4,22,23}, {21,22,2,3,16,19,6,7,8,9,10,11,14,15,12,13,1,17,18,0,20,5,4,23}, {17,16,18,3,4,5,6,2,15,9,10,12,11,13,14,8,1,0,23,19,20,21,22,7} }; vector<vector<int>>v5 = { {0,1,2,13,4,5,6,11,8,9,10,3,12,7,14,15,18,19,16,17,20,21,22,23}, {14,1,2,13,11,5,6,8,0,9,10,3,12,4,7,15,18,19,16,17,20,21,22,23}, {16,1,2,3,4,0,23,22,8,9,15,14,12,13,11,10,21,17,18,19,20,5,7,6} }; vector<vector<int>>v6 = { {0,9,2,3,4,15,6,7,8,5,10,11,12,13,14,1,16,17,18,19,22,23,20,21}, {0,9,10,3,4,12,15,7,8,6,5,11,2,13,14,1,16,17,18,19,22,23,20,21}, {0,4,19,18,20,5,6,7,13,12,10,11,9,8,14,15,16,1,3,2,17,21,22,23} }; CubeOpt op1(b, v1); CubeOpt op2(b, v2); CubeOpt op3(b, v3); CubeOpt op4(b, v4); CubeOpt op5(b, v5); CubeOpt op6(b, v6); vector<CubeOpt>opts = { op1,op2,op3,op4,op5,op6 }; Cube cube(b, opts); cube.bfs(2, 1, 24); return 0; }这个搜索范围已经到1-24了,还是搜不到答案。尝试了几种开放性尝试,也没效果。
于是我又开始思考新思路,很快,我就发现一个重要的规律:
为了确定新思路中新的复原顺序,先用代码测试一下:
int changeNum() { int ans = 0; for (int i = 0; i < v.size(); i++) { if (v.size() == 24) { if (typeId == 2) { if (v[i] != i)ans++; } else { if (v[i] / 4 != i /4)ans++; } } else { if (v[i] != i)ans++; } } return ans; } int main() { CubeBlock block1(0, 24);//24中心区棱块 CubeBlock block2(1, 24);//24中心区角块 CubeBlock block3(2, 24);//24侧边区侧棱 vector<CubeBlock>b = vector<CubeBlock>{ block1,block2,block3 }; mans[0] = "上", mans[1] = "下", mans[2] = "前", mans[3] = "后", mans[4] = "左", mans[5] = "右"; vector<vector<int>>v1 = { {2,3,0,1,4,5,6,7,20,9,10,11,16,13,14,15,8,17,18,19,12,21,22,23}, {2,3,0,1,4,5,6,7,20,21,10,11,16,17,14,15,8,9,18,19,12,13,22,23}, {4,5,6,7,0,1,2,3,11,8,9,10,12,13,14,15,16,17,18,19,20,21,22,23} }; vector<vector<int>>v2 = { {0,1,2,3,6,7,4,5,8,9,18,11,12,13,22,15,16,17,14,19,20,21,10,23}, {0,1,2,3,6,7,4,5,8,9,18,19,12,13,22,23,16,17,14,15,20,21,10,11}, {0,1,2,3,4,5,6,7,8,9,10,11,13,14,15,12,20,21,22,23,16,17,18,19} }; vector<vector<int>>v3 = { {0,1,17,3,4,5,23,7,10,11,8,9,12,13,14,15,16,6,18,19,20,21,22,2}, {0,1,17,18,4,5,20,23,10,11,8,9,12,13,14,15,16,7,6,19,3,21,22,2}, {0,1,2,6,21,20,22,7,8,14,13,11,12,10,9,15,16,17,18,3,5,4,19,23} }; vector<vector<int>>v4 = { {21,1,2,3,19,5,6,7,8,9,10,11,14,15,12,13,16,17,18,0,20,4,22,23}, {21,22,2,3,16,19,6,7,8,9,10,11,14,15,12,13,1,17,18,0,20,5,4,23}, {17,16,18,3,4,5,6,2,15,9,10,12,11,13,14,8,1,0,23,19,20,21,22,7} }; vector<vector<int>>v5 = { {0,1,2,13,4,5,6,11,8,9,10,3,12,7,14,15,18,19,16,17,20,21,22,23}, {14,1,2,13,11,5,6,8,0,9,10,3,12,4,7,15,18,19,16,17,20,21,22,23}, {16,1,2,3,4,0,23,22,8,9,15,14,12,13,11,10,21,17,18,19,20,5,7,6} }; vector<vector<int>>v6 = { {0,9,2,3,4,15,6,7,8,5,10,11,12,13,14,1,16,17,18,19,22,23,20,21}, {0,9,10,3,4,12,15,7,8,6,5,11,2,13,14,1,16,17,18,19,22,23,20,21}, {0,4,19,18,20,5,6,7,13,12,10,11,9,8,14,15,16,1,3,2,17,21,22,23} }; CubeOpt op1(b, v1); CubeOpt op2(b, v2); CubeOpt op3(b, v3); CubeOpt op4(b, v4); CubeOpt op5(b, v5); CubeOpt op6(b, v6); vector<CubeOpt>opts = { op1,op2,op3,op4,op5,op6 }; Cube cube(b, opts); cube.bfs(0, 1, 8); // or cube.bfs(1, 1, 8); return 0; }把2个搜索都试了一下,结果显示cube.bfs(1, 1, 8)更容易出结果,所以我们还是先复原中心区棱块再复原中心区角块。
4,复原方法(V3)
(1)复原角块和侧边区中棱
同V1
先复原8个角块。
然后复原侧边区中棱的公式:
0 1 2 3 5 4 7 6 8 9 10 11 0上 1下 2前 0上 1下 3后 效果是4567变成5476
0 3 2 1 4 5 7 6 8 9 10 11 0上 2前 0上 2前 0上 2前 效果是1367变成3176
0 1 2 3 7 5 4 6 8 9 10 11 0上 2前 0上 4左 0上 2前 0上 4左 效果是467变成746
(2)复原中心区棱块
同V1
6 1 0 3 4 5 2 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 0上 0上 0上 2前 2前 0上 2前 2前(2 6交换)
0 1 2 3 4 5 6 7 8 9 16 11 12 13 14 15 20 17 18 19 10 21 22 23 0上 2前 0上 0上 2前 2前 2前 0上(10 20 16轮换)
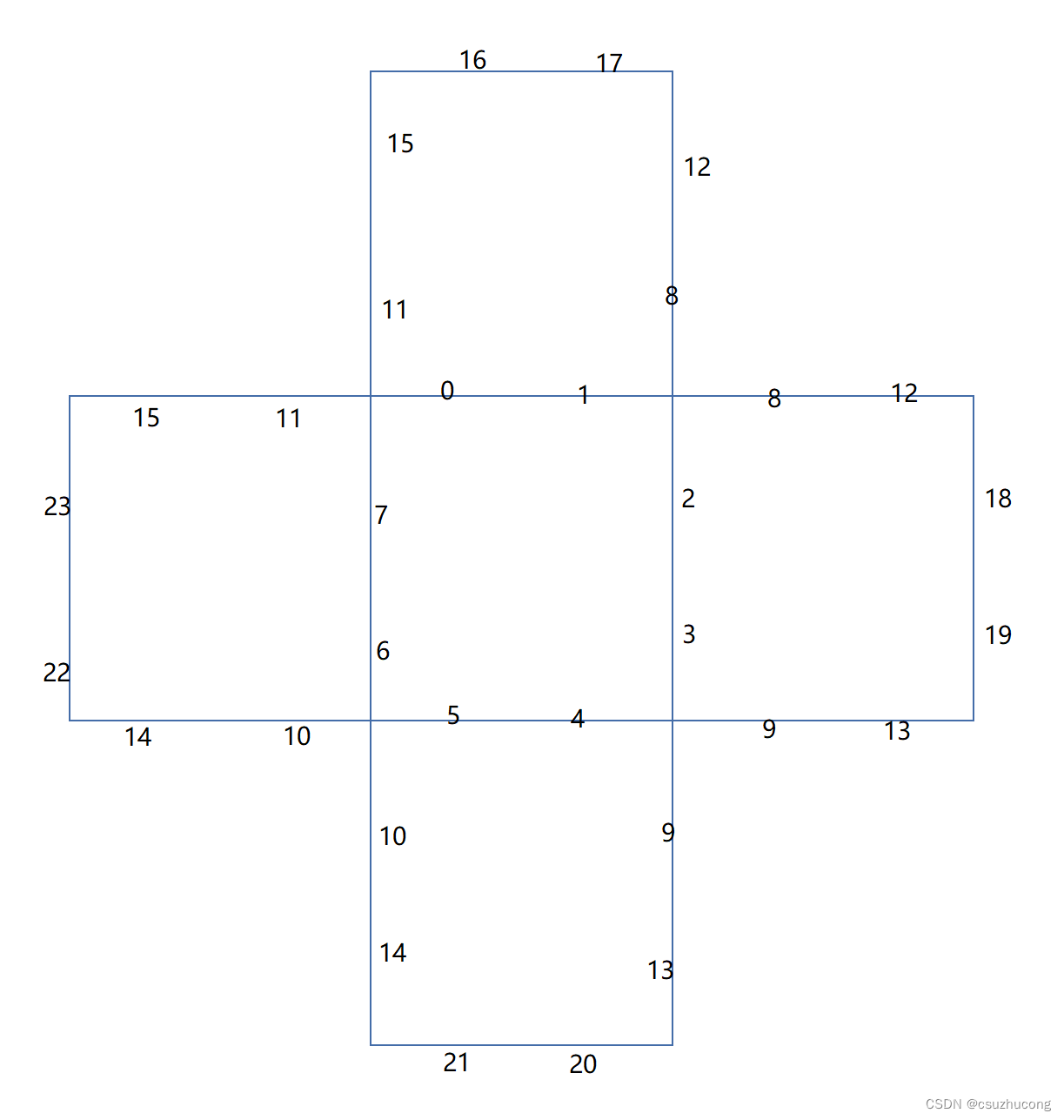
(3)复原侧边区侧棱
int changeNum() { int ans = 0; for (int i = 0; i < v.size(); i++) { if (typeId == 0) { if (i >= 8 && i < 16) { if (abs(v[i] - i) != 4)ans++; } else { if (v[i] / 2 != i / 2)ans++; } } else { if (v[i]/4 != i/4)ans++; } } return ans; } int main() { CubeBlock block1(0, 24);//24侧边区侧棱 CubeBlock block2(1, 24);//24中心区棱块 vector<CubeBlock>b = vector<CubeBlock>{ block1,block2 }; vector<vector<int>>v1 = { {4,5,6,7,0,1,2,3,11,8,9,10,12,13,14,15,16,17,18,19,20,21,22,23}, {2,3,0,1,4,5,6,7,20,9,10,11,16,13,14,15,8,17,18,19,12,21,22,23} }; vector<vector<int>>v2 = { {0,1,2,3,4,5,6,7,8,9,10,11,13,14,15,12,20,21,22,23,16,17,18,19}, {0,1,2,3,6,7,4,5,8,9,18,11,12,13,22,15,16,17,14,19,20,21,10,23} }; vector<vector<int>>v3 = { {0,1,2,6,21,20,22,7,8,14,13,11,12,10,9,15,16,17,18,3,5,4,19,23} , {0,1,17,3,4,5,23,7,10,11,8,9,12,13,14,15,16,6,18,19,20,21,22,2} }; vector<vector<int>>v4 = { {17,16,18,3,4,5,6,2,15,9,10,12,11,13,14,8,1,0,23,19,20,21,22,7}, {21,1,2,3,19,5,6,7,8,9,10,11,14,15,12,13,16,17,18,0,20,4,22,23} }; vector<vector<int>>v5 = { {16,1,2,3,4,0,23,22,8,9,15,14,12,13,11,10,21,17,18,19,20,5,7,6}, {0,1,2,13,4,5,6,11,8,9,10,3,12,7,14,15,18,19,16,17,20,21,22,23} }; vector<vector<int>>v6 = { {0,4,19,18,20,5,6,7,13,12,10,11,9,8,14,15,16,1,3,2,17,21,22,23}, {0,9,2,3,4,15,6,7,8,5,10,11,12,13,14,1,16,17,18,19,22,23,20,21} }; CubeOpt op1(b, v1); CubeOpt op2(b, v2); CubeOpt op3(b, v3); CubeOpt op4(b, v4); CubeOpt op5(b, v5); CubeOpt op6(b, v6); vector<CubeOpt>opts = { op1,op2,op3 }; mans[0] = "上", mans[1] = "下", mans[2] = "前", mans[3] = "", mans[4] = "", mans[5] = ""; Cube cube(b, opts); cube.bfs(0, 1, 8); return 0; }公式:
0,1,2,3,4,5,6,7,15,14,13,12,11,10,9,8,16,17,18,19,20,21,22,23, 0上 0上 1下 1下 2前 0上 0上 1下 1下 2前 2前 2前(8和15交换,9和14交换,10和13交换,11和12交换)
0,1,2,3,4,5,6,7,13,12,15,14,9,8,11,10,16,17,18,19,20,21,22,23, 0上 0上 0上 1下 2前 0上 0上 1下 1下 2前 0上 0上 2前 2前 0上 1下(8和13交换,9和12交换,10和15交换,11和14交换)
测一下第二个公式对中心区棱块的作用:
void test(vector<vector<int>>v, vector<int>id) { vector<int>x = v[0]; for (int i = 0; i < x.size(); i++)x[i] = i; for (auto k : id) { auto& vi = v[k]; auto tmp = x; for (int i = 0; i < x.size(); i++)x[i] = tmp[vi[i]]; } for (int i = 0; i < x.size(); i++)cout << x[i] << ","; } test({ v1[1], v2[1],v3[1] }, { 0,0,0,1,2,0,0,1,1,2,0,0,2,2 ,0,1});输出0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,18,17,16,19,22,21,20,23
虽然轮换对称意义下,没有改变中心区棱块,但和完全不变还是有区别的。
第一个公式同理,把这个放入代码,再套一层:
int main() { CubeBlock block1(0, 24);//24侧边区侧棱 CubeBlock block2(1, 24);//24中心区棱块 vector<CubeBlock>b = vector<CubeBlock>{ block1,block2 }; vector<vector<int>>v1 = { {4,5,6,7,0,1,2,3,11,8,9,10,12,13,14,15,16,17,18,19,20,21,22,23}, {2,3,0,1,4,5,6,7,20,9,10,11,16,13,14,15,8,17,18,19,12,21,22,23} }; vector<vector<int>>v2 = { {0,1,2,3,4,5,6,7,8,9,10,11,13,14,15,12,20,21,22,23,16,17,18,19}, {0,1,2,3,6,7,4,5,8,9,18,11,12,13,22,15,16,17,14,19,20,21,10,23} }; vector<vector<int>>v3 = { {0,1,2,6,21,20,22,7,8,14,13,11,12,10,9,15,16,17,18,3,5,4,19,23} , {0,1,17,3,4,5,23,7,10,11,8,9,12,13,14,15,16,6,18,19,20,21,22,2} }; vector<vector<int>>v4 = { {17,16,18,3,4,5,6,2,15,9,10,12,11,13,14,8,1,0,23,19,20,21,22,7}, {21,1,2,3,19,5,6,7,8,9,10,11,14,15,12,13,16,17,18,0,20,4,22,23} }; vector<vector<int>>v5 = { {16,1,2,3,4,0,23,22,8,9,15,14,12,13,11,10,21,17,18,19,20,5,7,6}, {0,1,2,13,4,5,6,11,8,9,10,3,12,7,14,15,18,19,16,17,20,21,22,23} }; vector<vector<int>>v6 = { {0,4,19,18,20,5,6,7,13,12,10,11,9,8,14,15,16,1,3,2,17,21,22,23}, {0,9,2,3,4,15,6,7,8,5,10,11,12,13,14,1,16,17,18,19,22,23,20,21} }; vector<vector<int>>v7 = { {0, 1, 2, 3, 4, 5, 6, 7, 15, 14, 13, 12, 11, 10, 9, 8, 16, 17, 18, 19, 20, 21, 22, 23} , {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23} }; vector<vector<int>>v8 = { {0,1,2,3,4,5,6,7,13,12,15,14,9,8,11,10,16,17,18,19,20,21,22,23} , {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23} }; CubeOpt op1(b, v1); CubeOpt op2(b, v2); CubeOpt op3(b, v3); CubeOpt op4(b, v4); CubeOpt op5(b, v5); CubeOpt op6(b, v6); CubeOpt op7(b, v7); CubeOpt op8(b, v8); vector<CubeOpt>opts = { op7,op8,op1,op3,op5 }; mans[0] = "上上下下前上上下下前前前", mans[1] = "上上上下前上上下下前上上前前上下", mans[2] = "上", mans[3] = "前", mans[4] = "左", mans[5] = ""; Cube cube(b, opts); cube.bfs(0, 1, 4); return 0; }0,1,2,3,4,5,6,7,12,15,14,13,8,11,10,9,16,17,18,19,20,21,22,23, 2上 0上上下下前上上下下前前前 4左 0上上下下前上上下下前前前 4左 2上 2上 4左 4左 2上(9和15交换,11和13交换)
继续套又可以得到:
0,1,2,3,4,5,6,7,12,10,9,15,8,14,13,11,16,17,18,19,20,21,22,23,
4左 0上上上下下前上上下下前前前左上上下下前上上下下前前前左上上左左上 4左 4左 4左(9 10交换,13 14交换)
然而,这几个公式加起来还是不够用,必须继续开发新公式才能解决所有情况。
PS:实际上24个侧边区侧棱可以分成三组,每一组8个,不同两组之间的块是不会交换位置的。
int main() { CubeBlock block1(0, 24);//24侧边区侧棱 CubeBlock block2(1, 24);//24中心区棱块 vector<CubeBlock>b = vector<CubeBlock>{ block1,block2 }; Opt opt1{ { {4,5,6,7,0,1,2,3,11,8,9,10,12,13,14,15,16,17,18,19,20,21,22,23}, {2,3,0,1,4,5,6,7,20,9,10,11,16,13,14,15,8,17,18,19,12,21,22,23} } ,"上" }; Opt opt2{ { {0,1,2,3,4,5,6,7,8,9,10,11,13,14,15,12,20,21,22,23,16,17,18,19}, {0,1,2,3,6,7,4,5,8,9,18,11,12,13,22,15,16,17,14,19,20,21,10,23} } ,"下" }; Opt opt3{ { {0,1,2,6,21,20,22,7,8,14,13,11,12,10,9,15,16,17,18,3,5,4,19,23} , {0,1,17,3,4,5,23,7,10,11,8,9,12,13,14,15,16,6,18,19,20,21,22,2} } ,"前" }; Opt opt4{ { {17,16,18,3,4,5,6,2,15,9,10,12,11,13,14,8,1,0,23,19,20,21,22,7}, {21,1,2,3,19,5,6,7,8,9,10,11,14,15,12,13,16,17,18,0,20,4,22,23} } ,"后" }; Opt opt5{ { {16,1,2,3,4,0,23,22,8,9,15,14,12,13,11,10,21,17,18,19,20,5,7,6}, {0,1,2,13,4,5,6,11,8,9,10,3,12,7,14,15,18,19,16,17,20,21,22,23} } ,"左" }; Opt opt6{ { {0,4,19,18,20,5,6,7,13,12,10,11,9,8,14,15,16,1,3,2,17,21,22,23}, {0,9,2,3,4,15,6,7,8,5,10,11,12,13,14,1,16,17,18,19,22,23,20,21} } ,"右" }; Opt opt7{ { {0, 1, 2, 3, 4, 5, 6, 7, 13, 11, 8, 14, 12, 10, 9, 15, 16, 17, 18, 19, 20, 21, 22, 23}, {0, 1, 2, 3, 4, 5, 6, 7, 12, 9, 8, 11, 10, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23}}, "0上 0上 2前 0上 0上 2前 2前 2前" }; Opt opt8{ { {0, 1, 2, 3, 4, 5, 6, 7, 15, 14, 8, 9, 12, 13, 11, 10, 16, 17, 18, 19, 20, 21, 22, 23}, {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 20, 17, 16, 19, 18, 21, 22, 23} }, "0上 0上 3左 0上 0上 3左 3左 3左" }; /* 0,1,2,3,4,5,6,7,8,14,13,11,9,15,12,10,16,17,18,19,20,21,22,23, 0,1,2,3,4,5,6,7,10,9,14,11,12,13,8,15,16,17,18,19,20,21,22,23, 1下 1下 2前 1下 1下 2前 2前 2前 0,1,2,3,4,5,6,7,8,9,15,14,11,10,12,13,16,17,18,19,20,21,22,23, 0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,18,17,22,19,20,21,16,23, 1下 1下 3左 1下 1下 3左 3左 3左 0,1,2,3,4,5,6,7,10,14,13,9,12,8,11,15,16,17,18,19,20,21,22,23, 0,1,2,3,4,5,6,7,10,9,12,11,8,13,14,15,16,17,18,19,20,21,22,23, 2前 0上 0上 2前 0上 0上 2前 2前 0,1,2,3,4,5,6,7,8,12,15,11,14,10,9,13,16,17,18,19,20,21,22,23, 0,1,2,3,4,5,6,7,14,9,8,11,12,13,10,15,16,17,18,19,20,21,22,23, 2前 1下 1下 2前 1下 1下 2前 2前 0,1,2,3,4,5,6,7,10,11,15,14,12,13,9,8,16,17,18,19,20,21,22,23, 0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,18,17,20,19,16,21,22,23, 3左 0上 0上 3左 0上 0上 3左 3左 0,1,2,3,4,5,6,7,8,9,13,12,14,15,11,10,16,17,18,19,20,21,22,23, 0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,22,17,16,19,20,21,18,23, 3左 1下 1下 3左 1下 1下 3左 3左 */ CubeOpt op1(b, opt1); CubeOpt op2(b, opt2); CubeOpt op3(b, opt3); CubeOpt op4(b, opt4); CubeOpt op5(b, opt5); CubeOpt op6(b, opt6); CubeOpt op7(b, opt7); CubeOpt op8(b, opt8); vector<CubeOpt>opts = { op7,op8,op1,op2,op3,op5 }; for (int i = 0; i < opts.size(); i++)mans[i] = opts[i].getName(); Cube cube(b, opts); cube.bfs(0, 1, 4); return 0; }(4)复原中心区角块
今天的文章
5阶齿轮魔方教程_二阶齿轮魔方公式七步还原分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/89848.html