前言
首先这是一份面向面试的算法题,题目主要选自leetcode中hot 100 | 腾讯精选50题 | 精选Top面试题 | 剑指offer | 面试中遇到的一些算法题,全文122题,基本涵盖了前端面试中的算法题分类。因为个人能力有限,所以题目几乎是easy | mid,并且搬运了一些优秀的题解均在参考文献中。如果对你有帮助的话点个👍和收藏吧❤️
目录
dp
思想
感觉很像时高中数列的思想,给出首项,以及一个递推式子,让你求任意项的值。
步骤基本是: 寻找状态转移方程 => 建立合适的数据结构表 => 填表
爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢
dp[0] = 0 dp[1] = 1 dp[2] = 2
dp[n] = dp[n-1] + dp[n-2] // 到达第n阶楼梯有从n-1阶走一步和从第n-2阶走两步两种情况
var climbStairs = function(n) {
let dp = [];
dp[0] = 0,dp[1] = 1,dp[2] = 2;
for(let i = 3;i <= n;i++){
dp[i] = dp[i-2] + dp[i-1];
}
return dp[n];
};
打家劫舍
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你在不触动警报装置的情况下,能够偷窃到的最高金额
// 动态规划方程:dp[n] = num + Max(dp[n-1])
// 由于不可以在相邻的房屋闯入,所以在当前位置 n 房屋可盗窃的最大值,要么就是 n-1 房屋可盗窃的最大值,要么就是 n-2 房屋可盗窃的最大值加上当前房屋的值,二者之间取最大值
// 举例来说:1 号房间可盗窃最大值为 33 即为 dp[1]=3,2 号房间可盗窃最大值为 44 即为 dp[2]=4,3 号房间自身的值为 22 即为 num=2,那么 dp[3] = MAX( dp[2], dp[1] + num ) = MAX(4, 3+2) = 5,3 号房间可盗窃最大值为 55
var rob = function(nums) {
if(nums.length === 0) return 0;
if(nums.length === 1) return nums[0];
if(nums.length === 2) return Math.max(nums[0],nums[1]);
let dp = [nums[0],Math.max(nums[0],nums[1])];
for(let i = 2;i < nums.length;i++){
dp[i] = Math.max(dp[i-1],dp[i-2]+nums[i]);
}
return Math.max(dp[nums.length-1],dp[nums.length-2]);
};
最大正方形
在一个由 0 和 1 组成的二维矩阵内,找到只包含 1 的最大正方形,并返回其面积
const maximalSquare = (matrix) => {
if (!matrix.length) return 0
let maxsqlen = 0
let rowLength = matrix.length, colLength = matrix[0].length
for (let row = 0; row < rowLength; row++) {
for (let col = 0; col < colLength; col++) {
if (matrix[row][col] === '1') {
matrix[row][col] = Number(matrix[row][col])
if (row != 0 && col != 0) {
matrix[row][col] = Math.min(matrix[row-1][col], matrix[row-1][col-1], matrix[row][col-1]) + 1
}
maxsqlen = Math.max(maxsqlen, matrix[row][col])
}
}
}
return maxsqlen**2
}
/** DP * 题目要求最大正方形面积,面积 = 边长 * 边长,也就是求最大正方形的边长 * 所以也就变成了,在矩阵中找最大正方形,矩阵中只有0|1两种值,全部为1的才是正方形 * 如何知道矩阵中哪里是1,哪里是0,只能穷举,但要聪明的穷举,这不就是动态规划的本质嘛! * 动态规划第一步,先假象我们创建了一个二维数组dp,用来存储「这个点为右下角的最大正方形的边长」 * 下面开始找 状态转换方程 * 思路:假设有如下矩阵 * 1 0 1 1 1 * 1 1 1 1 1 * 1 1 1 1 1 * 1 0 0 1 1 * 随便找一个点,直观地,我们先找最右下角的点,设该点的最大正方形边长为 dp[i][j], 我们用肉眼看一下,dp[i][j] 应该等于 2 * 为什么等于2,是因为我们看了 dp[i-1][j], dp[i-1][j-1], dp[i][j-1] 这三个点都为1,而又因为dp[i][j-2] 为0,所以 * 我们知道dp[i][j]最大就为2了。也就是我们不能只看dp[i][j]相邻的三个点,而应该看「这三个相邻点为正方形右下角」的边长情况, * 取最小边长进行求解 dp[i][j] 的最大正方形边长。(看,我们找到了重叠子问题和最优子结构) * 所以,状态转换方程为:dp[i][j] = Math.min(dp[i-1][j], dp[i-1][j-1], dp[i][j-1]) + 1 * 下一步,需要根据矩阵数据,进行选择和明确 base case 即可 */
零钱兑换
给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1
// dp[0] = 0 金额为零时不需要硬币
// dp[n] = min(dp[n],dp[n-coin1] + 1,dp[n-coin2],...) 金额为n时,硬币数等于(n-coin)+1中所需硬币最少的组合
var coinChange = function(coins, amount) {
let dp = new Array( amount + 1 ).fill( Infinity );
dp[0] = 0;
for (let i = 1; i <= amount; i++) {
for (let coin of coins) {
if (i - coin >= 0) {
dp[i] = Math.min(dp[i], dp[i - coin] + 1);
}
}
}
return dp[amount] === Infinity ? -1 : dp[amount];
}
不同路径
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
问总共有多少条不同的路径
var uniquePaths = function(m, n) {
if(m === 1 && n === 1) return 1;
let data = [],rows = [0];
for(let i = 0;i < n-1;i++){
rows.push(1);
}
data.push(rows);
for(let i = 0;i < m-1;i++){
data.push([1]);
}
for(let i = 1;i < m;i++){
for(let j = 1;j < n;j++){
data[i][j] = data[i-1][j] + data[i][j-1];
}
}
return data[m-1][n-1];
};
股票题状态机
本文就来告诉你这个框架,然后带着你一道一道秒杀。
这 6 道股票买卖问题是有共性的,我们通过对第四题(限制最大交易次数为 k)的分析一道一道解决。因为第四题是一个最泛化的形式,其他的问题都是这个形式的简化。
第一题是只进行一次交易,相当于 k = 1;第二题是不限交易次数,相当于 k = +infinity(正无穷);第三题是只进行 2 次交易,相当于 k = 2;剩下两道也是不限次数,但是加了交易「冷冻期」和「手续费」的额外条件,其实就是第二题的变种,都很容易处理。
一、穷举框架
首先,还是一样的思路:如何穷举?这里的穷举思路和上篇文章递归的思想不太一样。
递归其实是符合我们思考的逻辑的,一步步推进,遇到无法解决的就丢给递归,一不小心就做出来了,可读性还很好。缺点就是一旦出错,你也不容易找到错误出现的原因。比如上篇文章的递归解法,肯定还有计算冗余,但确实不容易找到。
而这里,我们不用递归思想进行穷举,而是利用「状态」进行穷举。我们具体到每一天,看看总共有几种可能的「状态」,再找出每个「状态」对应的「选择」。我们要穷举所有「状态」,穷举的目的是根据对应的「选择」更新状态。听起来抽象,你只要记住「状态」和「选择」两个词就行,下面实操一下就很容易明白了。
for 状态1 in 状态1的所有取值:
for 状态2 in 状态2的所有取值:
for ...
dp[状态1][状态2][...] = 择优(选择1,选择2...)
比如说这个问题,每天都有三种「选择」:买入、卖出、无操作,我们用 buy, sell, rest 表示这三种选择。但问题是,并不是每天都可以任意选择这三种选择的,因为 sell 必须在 buy 之后,buy 必须在 sell 之后。那么 rest 操作还应该分两种状态,一种是 buy 之后的 rest(持有了股票),一种是 sell 之后的 rest(没有持有股票)。而且别忘了,我们还有交易次数 k 的限制,就是说你 buy 还只能在 k > 0 的前提下操作。
很复杂对吧,不要怕,我们现在的目的只是穷举,你有再多的状态,老夫要做的就是一把梭全部列举出来。这个问题的「状态」有三个,第一个是天数,第二个是允许交易的最大次数,第三个是当前的持有状态(即之前说的 rest 的状态,我们不妨用 1 表示持有,0 表示没有持有)。然后我们用一个三维数组就可以装下这几种状态的全部组合:
dp[i][k][0 or 1]
0 <= i <= n-1, 1 <= k <= K
n 为天数,大 K 为最多交易数
此问题共 n × K × 2 种状态,全部穷举就能搞定。
for 0 <= i < n:
for 1 <= k <= K:
for s in {0, 1}:
dp[i][k][s] = max(buy, sell, rest)
而且我们可以用自然语言描述出每一个状态的含义,比如说 dp[3][2][1] 的含义就是:今天是第三天,我现在手上持有着股票,至今最多进行 2 次交易。再比如 dp[2][3][0] 的含义:今天是第二天,我现在手上没有持有股票,至今最多进行 3 次交易。很容易理解,对吧?
我们想求的最终答案是 dp[n – 1][K][0],即最后一天,最多允许 K 次交易,最多获得多少利润。读者可能问为什么不是 dp[n – 1][K][1]?因为 [1] 代表手上还持有股票,[0] 表示手上的股票已经卖出去了,很显然后者得到的利润一定大于前者。
记住如何解释「状态」,一旦你觉得哪里不好理解,把它翻译成自然语言就容易理解了。
二、状态转移框架
现在,我们完成了「状态」的穷举,我们开始思考每种「状态」有哪些「选择」,应该如何更新「状态」。只看「持有状态」,可以画个状态转移图。
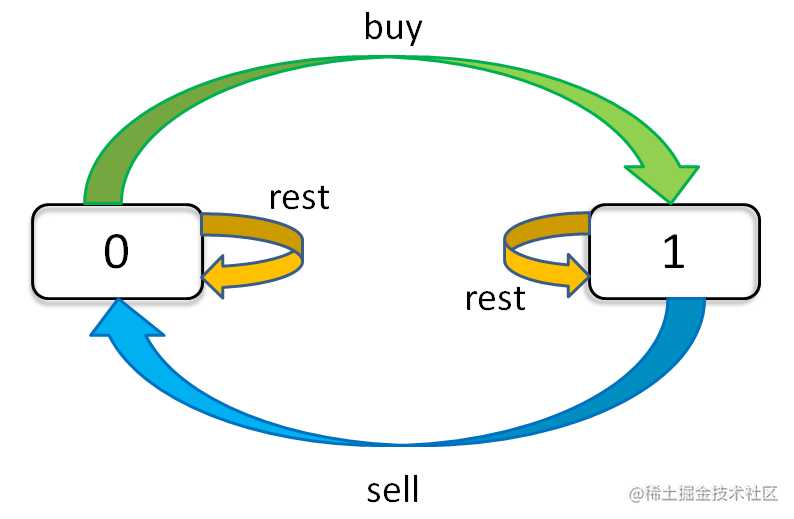
通过这个图可以很清楚地看到,每种状态(0 和 1)是如何转移而来的。根据这个图,我们来写一下状态转移方程:
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
max( 选择 rest , 选择 sell )
解释:今天我没有持有股票,有两种可能:
要么是我昨天就没有持有,然后今天选择 rest,所以我今天还是没有持有;
要么是我昨天持有股票,但是今天我 sell 了,所以我今天没有持有股票了。
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
max( 选择 rest , 选择 buy )
解释:今天我持有着股票,有两种可能:
要么我昨天就持有着股票,然后今天选择 rest,所以我今天还持有着股票;
要么我昨天本没有持有,但今天我选择 buy,所以今天我就持有股票了。
这个解释应该很清楚了,如果 buy,就要从利润中减去 prices[i],如果 sell,就要给利润增加 prices[i]。今天的最大利润就是这两种可能选择中较大的那个。而且注意 k 的限制,我们在选择 buy 的时候,把 k 减小了 1,很好理解吧,当然你也可以在 sell 的时候减 1,一样的。
现在,我们已经完成了动态规划中最困难的一步:状态转移方程。如果之前的内容你都可以理解,那么你已经可以秒杀所有问题了,只要套这个框架就行了。不过还差最后一点点,就是定义 base case,即最简单的情况。
如果你最多只允许完成一笔交易(即买入和卖出一支股票一次),设计一个算法来计算你所能获取的最大利润。
var maxProfit = function(prices) {
let dp_i_0 = 0,dp_i_1 = -Infinity;
for(let i = 0;i < prices.length;i++){
dp_i_0 = Math.max(dp_i_0,dp_i_1+prices[i]);
dp_i_1 = Math.max(dp_i_1,-prices[i]);
}
return dp_i_0;
};
买卖股票的最佳时机 II
1. 只要股票价格上涨,上涨的部分就是我的利润,可以理解为上涨期间第一天买入,然后一直持有到上涨最后一天即下跌前一天再卖出
2. 只要股票价格下跌,那我肯定在下跌前一天卖了,而且下跌期间永远不会买入
var maxProfit = function(prices) {
let profit = 0;
for (let i = 0; i < prices.length - 1; i++) {
if (prices[i + 1] > prices[i]) profit += prices[i + 1] - prices[i];
}
return profit;
};
贪心
思想
在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,他所做出的是在某种意义上的局部最优解最优解
剪绳子
给你一根长度为 n 的绳子,请把绳子剪成整数长度的 m 段(m、n都是整数,n>1并且m>1),每段绳子的长度记为 k[0],k[1]…k[m] 。请问 k[0]k[1]…*k[m] 可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。
var cuttingRope = function(number) {
if(number === 2 || number === 3) return number - 1;
let a = number % 3;
let b = parseInt(number / 3);
if(a === 0){
return 3 ** b;
}else if(a === 1){
return 2 * 2 * (3 ** (b - 1));
}else{
return 2 * (3 ** b);
}
};
跳跃游戏
给定一个非负整数数组,你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个位置。
1. 使用一个变量保存当前可到达的最大位置
2. 时刻更新最大位置
3. 可达位置小于数组长度返回false,反之即反
var canJump = function(nums) {
let k = 0;
for(let i = 0;i < nums.length;i++){
if(i > k) return false;
k = Math.max(k,i + nums[i]);
}
return true;
};
加油站
在一条环路上有 N 个加油站,其中第 i 个加油站有汽油 gas[i] 升。
你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。
如果你可以绕环路行驶一周,则返回出发时加油站的编号,否则返回 -1
1. gas - cost >= 0才能绕场一周,以此思想判断能否行驶一周
2. 从正确初始位置开始,拥有的汽油总是比消耗的汽油多,以此思想寻找初始位置
var canCompleteCircuit = function(gas, cost) {
let cur = 0,total = 0,start = 0;
for(let i = 0;i < gas.length;i++){
total += gas[i] - cost[i];
if(cur < 0){
cur = gas[i] - cost[i];
start = i;
}else cur += gas[i] - cost[i];
}
return total >= 0 ? start : -1;
};
二分
思想
针对有序数列进行查找时,优先考虑二分
输入一个非递减排序的数组的一个旋转,输出旋转数组的最小元素
// 例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转,该数组的最小值为1。
// NOTE:给出的所有元素都大于0,若数组大小为0,请返回0。
//把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。
//10111
1. 原数据为旋转数组,所以分界点前后都是有序的
2. 进行二分查找,注意因为找最小值,high赋值时应该从mid开始取,mid可能是最小值
function minNumberInRotateArray(rotateArray) {
if(!rotateArray.length) return 0;
let left = 0,right = rotateArray.length-1;
while(left < right){
let mid = Math.floor((right+left) >> 1);
if(rotateArray[left] <= rotateArray[right]){
return rotateArray[left];
}
if(rotateArray[left] < rotateArray[mid]){
left = mid + 1;
}else if(rotateArray[right] > rotateArray[mid]){
right = mid;
}else{
left++;
}
}
}
统计一个数字在排序数组中出现的次数
function GetNumberOfK(data, k) {
let low = 0,high = data.length-1;
let pos,count = 0;
while(low < high){
let mid = Math.floor((low+high)>>1);
if(data[mid] === k){
pos = mid;
break;
}else if(data[mid] < k){
low = mid + 1;
}else{
high = mid-1;
}
}
if(pos !== undefined){
count++;
let left = pos,right = pos;
while(left--){
if(data[left] === k){
count++;
}else{
break;
}
}
while(right++){
if(data[right] === k){
count++;
}else{
break;
}
}
return count;
}else return 0;
}
0~n-1中缺失的数字
一个长度为n-1的递增排序数组中的所有数字都是唯一的,并且每个数字都在范围0~n-1之内。在范围0~n-1内的n个数字中有且只有一个数字不在该数组中,请找出这个数字
var missingNumber = function(nums) {
let left = 0,
right = nums.length - 1;
while (left <= right) {
let mid = Math.floor((left + right) / 2);
if (mid === nums[mid]) {
left = mid + 1;
} else if (mid < nums[mid]) {
right = mid - 1;
}
}
return left;
};
最长上升子序列
1. 维护一个子序列存放当前的上升序列
2. 将当前数与子序列最大值比较,如果比最大值大之间加入队尾,如果更新则找一个合适的位置替换当前位置的元素
var lengthOfLIS = function(nums) {
let n = nums.length;
if(n <= 1){
return n;
}
let tail = [nums[0]];
for(let i = 0;i < n;i++){
if(nums[i] > tail[tail.length-1]){
tail.push(nums[i]);
}else{
let left = 0;
let right = tail.length-1;
while(left < right){
let mid = (left + right) >> 1;
if(tail[mid] < nums[i]){
left = mid + 1;
}else{
right = mid;
}
}
tail[left] = nums[i];
}
}
return tail.length;
};
搜索二维矩阵 II
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target。该矩阵具有以下特性:
每行的元素从左到右升序排列。 每列的元素从上到下升序排列。
输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
1. 选取左下角的值作为初始值key
2. 如果目标值大于key,因为是最左边的值(最小),所以col++
3. 如果目标值小于,那么更小的值只可能是上一行,所以row--
function Find(target,array){
let rows = array.length;
if(rows <= 0) return false;
let cols = array[0].length;
if(cols <= 0) return false;
let row = rows - 1;
let col = 0;
while(row >= 0 && col < cols){
if(array[row][col] > target){
row--;
}else if(array[row][col] < target){
col++;
}else{
return true;
}
}
return false;
}
Pow(x, n)
实现 pow(x, n) ,即计算 x 的 n 次幂函数
//快速幂算法
var myPow = function(x, n) {
if (!x) return 0;
if (x === 1) return 1;
if (x === -1) return (n & 1) ? -1 : 1;
if (n == 2147483647) return 0;
if (n == -2147483648) return x === 2 ? 0 : 1;
if (n < 0) {
x = 1 / x;
n = -n;
}
let res = 1;
while(n) {
if (n & 1) res *= x;
x *= x;
n >>= 1;
}
return res;
}
求交集
function intersection(...args){
if(!args.length) return [];
let res = [],left = args[0][0],right = args[0][1];
for(let i = 1;i < args.length;i++){
if(right >= args[i][0] || left <= args[i][1]){
left = Math.max(left,args[i][0]);
right = Math.min(right,args[i][1]);
res = [left,right];
}else{
return [];
}
}
return res;
}
回溯算法
解题思路
-
全局变量:保存结果
-
参数:递归函数的参数选择,通常是两种参数。
- 状态变量: result需要保存的值
- 条件变量: 判断搜索是否完毕以及搜索是否合法
-
完成条件: 完成条件是决定状态变量和条件变量取何值时可以判断整个搜索流程结束。整个搜索流程结束有两个含义:搜索成功并保存结果何搜索失败并返回上一次状态。
-
递归过程: 传递当前状态给下一次递归进行搜索。
模板
let res = []; //存储结果
function backtrack(path,condition,...){
if(judge(condition)){ //满足条件
res.push(path);
return;
}
for(let select of selectList){
if(剪枝条件) break;
path.push(select); // 走某条路
backtrack(path,newSelectList);
path.pop(); //返回上一个十字路口
}
}
适用场景
- 排列,组合
- 数组,字符串,给定一个特定的规则,尝试找到某个解
- 二维数组下的DFS搜索
怎么套用模板
我筛选了leetCode中hot和面试常考题库中关于回溯的题目,题目由易到难,覆盖每个使用场景。
子集
给定一组不含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
- 定义res数组存储结果
- 每个子集为状态变量,集合的元素个数为条件变量
- 子集的元素数量小于等于集合的元素数量为限制条件,满足条件时添加到结果数组,否则回退到上一步
- 下一层搜索的集合需要去掉已添加到状态变量中的元素
var subsets = function(nums) {
let res = [];
let n = nums.length;
function back(path,i){
if(i <= n){
res.push(path);
}
for(let j = i;j < n;j++){
path.push(nums[j]);
back(path.slice(0),j+1);
path.pop();
}
}
back([],0);
return res;
};
针对这道题还有一种比较酷的解法,利用二进制
-
一个集合的右2^n个子集
-
使用二进制模拟,每位为取或不取
-
举个例子:[1,2,3] => 符号位: 001 010 100 => 0-7与之&
=> [] [001] [010] [001,010] [100] [001,100] [010,100] [001,010,100] 刚好八种,并且对应数组下标。
var subsets = function(nums) {
let n = 1 << nums.length;
let res = [];
for(let i = 0;i < n;i++){
let temp = [];
for(let j = 0;j < nums.length;j++){
if(i & (1 << j)){
temp.push(nums[j]);
}
}
res.push(temp);
}
return res;
};
全排列
给定一个 没有重复 数字的序列,返回其所有可能的全排列。
- 定义res
- 每个排列序列为状态变量,排列序列中集合的个数为条件变量
- 当排列序列的元素个数等于给定序列时,满足条件
- 下一层递归依赖于上一层递归传递的路径
var permute = function(nums) {
let len = nums.length;
let res = [];
function back(path){
if(path.length === len){
res.push(path);
return;
}
for(let i = 0;i < len;i++){
if(path.indexOf(nums[i]) === -1){ //这里的判断很精髓
path.push(nums[i]);
back(path.slice());
path.pop();
}
}
}
back([]);
return res;
};
组合总和
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的数字可以无限制重复被选取。
- 定义res
- 每个子数组为状态变量,目标值为条件变量
- 子数组中的值相加等于目标值则满足要求
- 下一层递归的tar(与目标值相差的数目)依赖于上一层递归的选择
var combinationSum = function(candidates, target) {
let res = [];
let len = candidates.length;
//这里排序是为了防止在for循环if判断时直接跳出了,比如这样的样例[8,7,4,3],11
candidates.sort((x,y) => x-y);
function back(path,i,tar){
if(tar === 0){
res.push(path);
return;
}
for(let j = i;j < len;j++){
//判断是否当前的路口都是通向死路
if(tar < candidates[j]) break;
path.push(candidates[j]);
back(path.slice(),j,tar-candidates[j]);
path.pop();
}
}
back([],0,target);
return res;
};
分割回文串
给定一个字符串 s,将 s 分割成一些子串,使每个子串都是回文串。
返回 s 所有可能的分割方案。
- 定义res
- 状态变量为回文子串集,条件变量为子串集的字符串数目
- 当子串集的字符串数目与目标串长度相同时,满足要求
- 下层递归的开始位置由上层递归决定
var partition = function(str){
let res = [];
function isPalindrome(s){
let head = 0;
let tail = s.length-1;
while(head <= tail){
if(s[head] !== s[tail]) return false;
head++;
tail--;
}
return true;
}
function backtrack(path,start){
if(start === str.length) res.push(path);
for(let i = start;i < str.length;i++){
if(!isPalindrome(str.slice(start,i+1))) continue;
path.push(str.slice(start,i+1));
backtrack(path.slice(),i+1);
path.pop();
}
}
backtrack([],0);
return res;
}
单词搜索
给定一个二维网格和一个单词,找出该单词是否存在于网格中。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
- 状态变量为一条通路,条件变量为通路的长度
- 当通路与目标词汇长度一致时,满足条件
- 下一层递归的初始坐标和通路长度由上层递归决定
var exist = function (board, word) {
//越界处理
board[-1] = []
board.push([])
//寻找首个字母
for (let y = 0; y < board.length; y++) {
for (let x = 0; x < board.length; x++) {
if (word[0] === board[y][x] && backtrack(y, x, 0)) return true
}
}
//回溯
function backtrack(y, x, i) {
//回溯终止
if (i + 1 === word.length) return true
//保存字母
var tmp = board[y][x]
board[y][x] = false
if (board[y][x + 1] === word[i + 1] && backtrack(y, x + 1, i + 1)) return true
if (board[y][x - 1] === word[i + 1] && backtrack(y, x - 1, i + 1)) return true
if (board[y + 1][x] === word[i + 1] && backtrack(y + 1, x, i + 1)) return true
if (board[y - 1][x] === word[i + 1] && backtrack(y - 1, x, i + 1)) return true
//复原字母
board[y][x] = tmp
}
return false
};
复原IP地址
给定一个只包含数字的字符串,复原它并返回所有可能的 IP 地址格式。
有效的 IP 地址正好由四个整数(每个整数位于 0 到 255 之间组成),整数之间用 ‘.’ 分隔。
var restoreIpAddresses = function(s) {
let res = [];
if(s.length < 4 || s.length > 12) return res;
function dfs(s, sub, index) {
if(s.length === 0 && index === 4) res.push(sub.slice(1)); // 去掉开头的.
if(s.length === 0 || index === 4) return;
// 一个数
dfs(s.slice(1), `${sub}.${s.slice(0,1)}`, index + 1);
if(s[0] !== '0' && s.length > 1) {
dfs(s.slice(2), `${sub}.${s.slice(0,2)}`, index + 1); // 两个数
if(s.length > 2 && parseInt(s.slice(0,3)) <= 255) {
dfs(s.slice(3), `${sub}.${s.slice(0,3)}`, index + 1); //三个数
}
}
}
dfs(s, '', 0);
return res;
};
排序算法
冒泡排序
比较两个记录键值的大小,如果这两个记录键值的大小出现逆序,则交换这两个记录

function bubbleSort(arr){
for(let i = 1;i < arr.length;i++){
for(let j = i;j > 0;j--){
if(arr[j] < arr[j-1]){
[arr[j],arr[j-1]] = [arr[j-1],arr[j]];
}
}
}
return arr;
}
快排
在n个记录中取某一个记录的键值为标准,通常取第一个记录键值为基准,通过一趟排序将待排的记录分为小于或等于这个键值的两个独立的部分,这是一部分的记录键值均比另一部分记录的键值小,然后,对这两部分记录继续分别进行快速排序,以达到整个序列有序

function quickSort(arr){
if(arr.length <= 1) return arr;
let right = [],left = [],keys = arr.shift();
for(let value of arr){
if(value > keys){
right.push(value)
}else{
left.push(value);
}
}
return quickSort(left).concat(keys,quickSort(right));
}
插入排序
第i(i大于等于1)个记录进行插入操作时,R1、 R2,…,是排好序的有序数列,取出第i个元素,在序列中找到一个合适的位置并将她插入到该位置上即可。

function insertSort(arr){
for(let i = 1;i < arr.length;i++){
let j = i-1;
if(arr[i]<arr[j]){
let temp = arr[i];
while(j >= 0 && temp < arr[j]){
arr[j+1] = arr[j];
j--;
}
arr[j+1] = temp;
}
}
return arr;
}
希尔排序
算法先将要排序的一组数按某个增量d(n/2,n为要排序数的个数)分成若干组,每组中记录的下标相差d.对每组中全部元素进行直接插入排序,然后再用一个较小的增量(d/2)对它进行分组,在每组中再进行直接插入排序。当增量减到1时,进行直接插入排序后,排序完成。

function hillSort(arr){
let len = arr.length;
for(let gap = parseInt(len >> 1);gap >= 1;gap = parseInt(gap >> 1)){
for(let i = gap;i < len;i++){
if(arr[i] < arr[i-gap]){
let temp = arr[i];
let j = i - gap;
while(j >= 0 && arr[j] > temp){
arr[j+gap] = arr[j];
j -= gap;
}
arr[j+gap] = temp;
}
}
}
return arr;
}
选择排序
在第i次选择操作中,通过n-i次键值间比较,从n-i+1个记录中选出键值最小的记录,并和第i(1小于等于1小于等于n-1)个记录交换

function selectSort(arr){
for(let i = 0;i < arr.length;i++){
let min = Math.min(...arr.slice(i));
let index = arr.indexOf(min);
[arr[i],arr[index]] = [arr[index],arr[i]];
}
return arr;
}
堆排序

function adjustMaxHeap(heap,head,heapSize){
let temp = heap[head];
let child = head * 2 + 1;
while(child < heapSize){
if(child+1 < heapSize && heap[child] < heap[child+1]) child++;
if(heap[head] < heap[child]){
heap[head] = heap[child];
head = child;
child = head * 2 + 1;
}else break;
heap[head] = temp;
}
}
function buildHeap(heap){
for(let i = (heap.length-1) >> 1;i >= 0;i--){
adjustMaxHeap(heap,i,heap.length);
}
}
function heapSort(arr){
buildHeap(arr);
for(let i = arr.length-1;i > 0;i--){
[arr[i],arr[0]] = [arr[0],arr[i]];
adjustMaxHeap(arr,0,i);
}
return arr;
}
归并排序
把一个有n个记录的无序文件看成是由n个长度为1的有序子文件组成的文件,然后进行两两归并

function MergeSort(arr,left,right){
if(left >= right) return;
let mid = Math.floor((right - left) >> 1) + left;
MergeSort(arr,left,mid);
MergeSort(arr,mid+1,right);
Merge(arr,left,mid,right);
return arr;
}
function Merge(arr,left,mid,right){
let temp = [],i = 0;
let p1 = left,p2 = mid + 1;
while(p1 <= mid && p2 <= right){
arr[p1] <= arr[p2] ? temp[i++] = arr[p1++] : temp[i++] = arr[p2++];
}
while(p1 <= mid){
temp[i++] = arr[p1++];
}
while(p2 <= right){
temp[i++] = arr[p2++];
}
for(let i = 0;i < temp.length;i++){
arr[i+left] = temp[i];
}
}
桶排序
把数据分组,放在一个个的桶中,然后对每个桶里面的在进行排序
function radixSort(arr,arrDomain,gropSize){
let data = [];
for(let i = 0;i < arr.length;i++) data.push([]);
console.log(data)
for(let i = 0;i < arr.length;i++){
data[Math.floor(parseInt(arr[i] / gropSize)) + 1].push(arr[i]);
}
for(let i = 0;i < data.length;i++){
quickSort(data[i]);
}
return data.flat(Infinity);
}
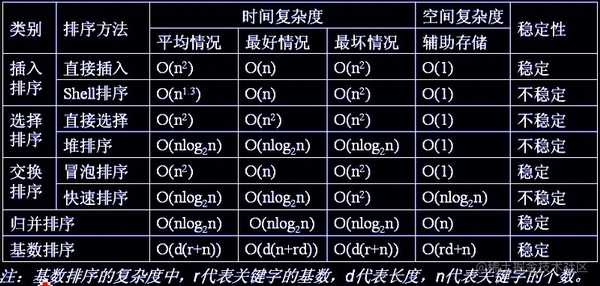
各排序算法的稳定性,时间复杂度,空间复杂度
系统自带排序实现
每个语言的排序内部实现都是不同的。
对于 JS 来说,数组长度大于 10 会采用快排,否则使用插入排序。选择插入排序是因为虽然时间复杂度很差,但是在数据 量很小的情况下和 O(N * logN) 相差无几,然而插入排序需要的常数时间很小,所以相对别的排序来说更快。
稳定性
稳定性的意思就是对于相同值来说,相对顺序不能改变。通俗的讲有两个相同的数 A 和 B,在排序之前 A 在 B 的前面, 而经过排序之后,B 跑到了 A 的前面,对于这种情况的发生,我们管他叫做排序的不稳定性。
稳定性有什么意义?个人理解对于前端来说,比如我们熟知框架中的虚拟 DOM 的比较,我们对一个“列表进行渲染, 当数据改变后需要比较变化时,不稳定排序或操作将会使本身不需要变化的东西变化,导致重新渲染,带来性能的损耗。
排序面试题目
- 快速排序在完全无序的情况下效果最好,时间复杂度为O(nlogn),在有序情况下效果最差,时间复杂度为O(n^2)。
- 外部排序常用的算法是归并排序。
- 数组元素基本有序的情况下,插入排序效果最好,因为这样只需要比较大小,不需要移动,时间复杂度趋近于O(n)。
- 如果只想得到1000个元素组成的序列中第5个最小元素之前的部分排序的序列,用堆排序方法最快。
- 对长度为 n 的线性表作快速排序,在最坏情况下,比较次数为 n(n-1)/2。
练习题
排序链表
在 O(n log n) 时间复杂度和常数级空间复杂度下,对链表进行排序。
var sortList = function(head) {
let mergeList = (left,right) => {
let res = new ListNode(0);
let pre = res;
while(left && right){
if(left.val <= right.val){
pre.next = left;
left = left.next;
}else{
pre.next = right;
right = right.next;
}
pre = pre.next;
}
pre.next = left ? left : right;
return res.next;
}
let mergeSort = (node) => {
if(!node || !node.next) return node;
let mid = node;
let fast = node.next;
while(fast && fast.next){
mid = mid.next;
fast = fast.next.next;
}
let rightList = mid.next;
mid.next = null;
let left = node;
let right = rightList;
return mergeList(mergeSort(left),mergeSort(right));
}
return mergeSort(head);
};
逆序对
在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P%1000000007
let count = 0;
function InversePairs(data) {
if (data == null || data.length == 0) {
return 0;
}
MergeSort(data,0,data.length-1);
return count % 1000000007;
}
function MergeSort(arr,left,right){
if(left >= right) return;
let mid = Math.floor((right - left)>>1) + left;
MergeSort(arr,left,mid);
MergeSort(arr,mid+1,right);
Merge(arr,left,mid,right);
}
function Merge(arr,left,mid,right) {
let temp = [],i = 0;
let p1 = left,p2 = mid + 1;
while(p1 <= mid && p2 <= right){
if(arr[p1] <= arr[p2]){
temp[i++] = arr[p1++];
}else{
count += mid - p1 + 1;
temp[i++] = arr[p2++];
}
}
while(p1 <= mid){
temp[i++] = arr[p1++];
}
while(p2 <= right){
temp[i++] = arr[p2++];
}
for(let i = 0;i < temp.length;i++){
arr[i+left] = temp[i];
}
}
并查集
属于一种特殊的数据结构,在解决连通域问题上有着不错的性能。
三个组件
-
维护一个数组
let parents = [],存放当前节点的父节点,根节点的父节点是它本身。 -
查询一个节点的根节点是哪个节点。
function find(root){ let temp,son = root; while(root !== parents[root]){ root = parents[root]; } while(son !== root){ //路径压缩,其实就是个扁平化处理的过程 temp = parents[son]; parents[son] = root; son = temp; } return root; } //递归版 function find(root){ if(root !== parents[root]) parents[root] = find(parents[root]); return parents[root]; } -
合并两个连通域
function join(x,y){ x = find(x); y = find(y); if(x !== y){ parents[x] = y; } }
练习题
岛屿数量
- 写三大组件,初始话parents时将其键和值对应
- 判定当前节点四周是否存在陆地,如果有就将他们连接起来,如果没有就将当前节点的父节点置反
- 求出parents数组中键和值依然相等的数目(即为连通域的数目)
var numIslands = function(grid) {
let row = grid.length;
if(row === 0) return 0;
let col = grid[0].length;
let parents = [];
for(let i = 0;i < row;i++){
for(let j = 0;j < col;j++){
parents[i*col+j] = i * col + j;
}
}
function find(root){
if(root !== parents[root]) parents[root] = find(parents[root]);
return parents[root];
}
function union(x,y){
x = find(x);
y = find(y);
if(x !== y){
parents[x] = y;
}
}
for(let i = 0;i < row;i++){
for(let j = 0;j < col;j++){
if(grid[i][j] === '1'){
i < row-1 && grid[i+1][j] === '1' && union((i+1)*col+j,i*col+j);
j < col-1 && grid[i][j+1] === '1' && union(i*col+j+1,i*col+j);
}else{
parents[i*col+j] = -parents[i*col+j];
}
}
}
return parents.filter((value,key) => (key === value && Object.is(key,value))).length;
};
DFS的解法
var numIslands = function(grid) {
const row = grid.length;
if(!row) return 0;
const col = grid[0].length;
let res = 0;
for(let i = 0; i < row; i++) {
for(let j = 0; j < col; j++) {
if(grid[i][j] === '1') {
res++;
dfs(grid, i, j);
}
}
}
function dfs(grid, i, j) {
if(i < 0 || i >= row || j < 0 || j >= col) return;
if(grid[i][j] === '1') {
grid[i][j] = '0';
dfs(grid, i - 1, j);
dfs(grid, i + 1, j);
dfs(grid, i, j - 1);
dfs(grid, i, j + 1);
}
}
return res;
};
被围绕的区域
- 写三大组件
- 将
O节点划分为内部节点和边界节点,引入一个虚拟边界root节点 - 判定
O节点是否为内部节点,如果是则替换为X
var solve = function(board) {
let row = board.length;
if(row === 0) return board;
let col = board[0].length;
let parents = [];
for(let i = 0;i < row;i++){
for(let j = 0;j < col;j++){
parents[i*col+j] = i * col + j;
}
}
function find(root){
if(root !== parents[root]) parents[root] = find(parents[root]);
return parents[root];
}
function union(x,y){
x = find(x);
y = find(y);
if(x !== y){
parents[x] = y;
}
}
function isConnected(x,y){
return find(x) === find(y);
}
let virtualArea = row * col + 1;
for(let i = 0;i < row;i++){
for(let j = 0;j < col;j++){
if(board[i][j] === 'O'){
if(i === 0 || i === row-1 || j === 0 || j === col-1){
union(i*col+j,virtualArea);
}else{
i > 0 && board[i-1][j] === 'O' && union(i*col+j,(i-1)*col+j);
i < row-1 && board[i+1][j] === 'O' && union(i*col+j,(i+1)*col+j);
j > 0 && board[i][j-1] === 'O' && union(i*col+j,i*col+j-1);
j < col-1 && board[i][j+1] === 'O' && union(i*col+j,i*col+j+1);
}
}
}
}
for(let i = 0;i < row;i++){
for(let j = 0;j < col;j++){
if(board[i][j] === 'O' && !isConnected(i*col+j,virtualArea)){
board[i][j] = 'X';
}
}
}
return board;
};
拓扑排序
对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若边<u,v>∈E(G),则u在线性序列中出现在v之前。通常,这样的线性序列称为满足拓扑次序(Topological Order)的序列,简称拓扑序列。简单的说,由某个集合上的一个偏序得到该集合上的一个全序,这个操作称之为拓扑排序。不得不说百科的解释很专业,但就是不知道在说什么(wtcl)。
举个例子
- 对于有向无环图,我们首先找到一个入度为0的节点(随便找一个)
- 删除该节点,并将该节点的值存入结果数组,然后将该节点的所有邻接节点的入度减1
- 重新寻找一个入度为0的节点,再重复操作2
- 将剩余所有的入度为0的节点的值存入结果数组。
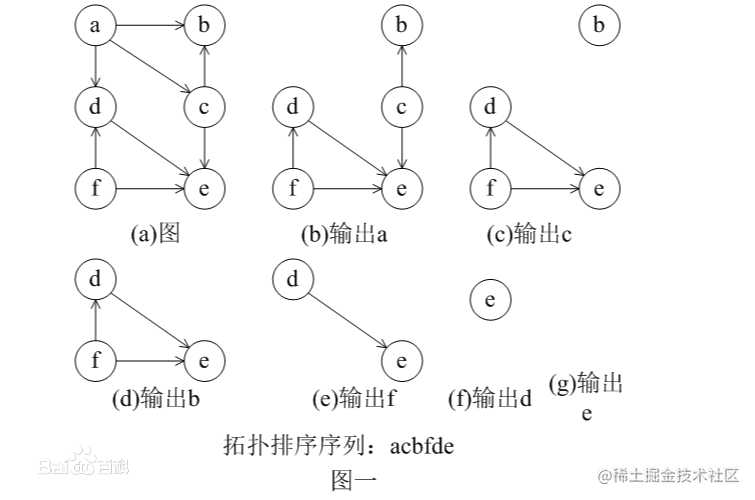
怎么建图
拓扑排序中涉及到节点的删除,所以采用邻接表的数据结构来表示图是比较不错的选择
邻接表
//这里是一个简单的邻接表(面向试题编程),该结构在练习题部分有
class Node{
constructor(value){
this.value = value;
this.next = null;
this.in = 0; //记录入度
}
}
class Graph{
constructor(nodeNum,edges){
this.list = new Array(nodeNum);
for(let i = 0;i < this.list.length;i++){ //初始化邻接表
this.list[i] = new Node(i);
}
let v1,v2,newNode = null;
for(let edge of edges){ //构建邻接表以及每个节点的入度数
[v2,v1] = edge;
newNode = new Node(v2);
newNode.next = this.list[v1].next;
this.list[v1].next = newNode;
this.list[v2].in++;
}
}
}
喜闻乐见的练习题
课程表 II
现在你总共有 n 门课需要选,记为 0 到 n-1。
在选修某些课程之前需要一些先修课程。 例如,想要学习课程 0 ,你需要先完成课程 1 ,我们用一个匹配来表示他们: [0,1]
给定课程总量以及它们的先决条件,返回你为了学完所有课程所安排的学习顺序。
可能会有多个正确的顺序,你只要返回一种就可以了。如果不可能完成所有课程,返回一个空数组。
- 建立邻接表
- 创建一个辅助栈存放入度为零的节点,一个存放结果的结果数组res和一个记录删除节点数目的计数器count
- 每次取辅助栈中的节点,将其所有的邻接节点入度减一并判断入度是否为零(从而添加到辅助栈中),将节点值放入res,count++
- 判定计数器是否与图的节点数相同,不相同证明有回路,按题目要求返回值就好
class Node{
constructor(value){
this.value = value;
this.next = null;
this.in = 0;
}
}
class Graph{
constructor(nodeNum,edges){
this.list = new Array(nodeNum);
for(let i = 0;i < this.list.length;i++){
this.list[i] = new Node(i);
}
let v1,v2,newNode = null;
for(let edge of edges){
[v2,v1] = edge;
newNode = new Node(v2);
newNode.next = this.list[v1].next;
this.list[v1].next = newNode;
this.list[v2].in++;
}
}
}
var findOrder = function(numCourses, prerequisites) {
let list = new Graph(numCourses,prerequisites).list;
let stack = [],res = [];
for(let node of list){
node.in === 0 && stack.push(node);
}
let count = 0;
while(stack.length){
let node = stack.pop();
count++;
res.push(node.value);
while(node.next){
(--list[node.next.value].in) === 0 && stack.push(list[node.next.value]);
node = node.next;
}
}
if(count !== list.length) return [];
else return res;
};
课程表
你这个学期必须选修 numCourse 门课程,记为 0 到 numCourse-1 。
在选修某些课程之前需要一些先修课程。 例如,想要学习课程 0 ,你需要先完成课程 1 ,我们用一个匹配来表示他们:[0,1]
给定课程总量以及它们的先决条件,请你判断是否可能完成所有课程的学习?
//上题的简化版,直接看代码吧
class Node{
constructor(value){
this.value = value;
this.next = null;
this.in = 0;
}
}
class Graph{
constructor(nodeNum,edges){
this.list = new Array(nodeNum);
for(let i = 0;i < this.list.length;i++){
this.list[i] = new Node(i);
}
let v1,v2,newNode = null;
for(let edge of edges){
[v2,v1] = edge;
newNode = new Node(v2);
newNode.next = this.list[v1].next;
this.list[v1].next = newNode;
this.list[v2].in++;
}
}
}
var canFinish = function(numCourses, prerequisites) {
let list = new Graph(numCourses,prerequisites).list;
let stack = [];
for(let node of list){
node.in === 0 && stack.push(node);
}
let count = 0;
while(stack.length){
let node = stack.pop();
count++;
while(node.next){
(--list[node.next.value].in) === 0 && stack.push(list[node.next.value]);
node = node.next;
}
}
return count === list.length
};
位运算
二进制中1的个数
请实现一个函数,输入一个整数,输出该数二进制表示中 1 的个数。例如,把 9 表示成二进制是 1001,有 2 位是 1。因此,如果输入 9,则该函数输出 2
//n & (n-1)每次1的数量--
var hammingWeight = function(n) {
let count = 0;
while(n){
count++;
n = n & (n-1);
}
return count;
};
数组中有一个数字出现的次数超过数组长度的一半,请找出这个数字
// 例如输入一个长度为9的数组{1,2,3,2,2,2,5,4,2}。由于数字2在数组中出现了5次,超过数组长度的一半,因此输出2。如果不存在则输出0。
1. count初始化为0,count === 0时,res = 当前数,count++
2. 当前数与res相同count++,否则count--
3. 以上两步能够选出出现次数最多的数,接下来判断它是否超过一半即可
function MoreThanHalfNum_Solution(numbers) {
let result,count=0;
for(let i = 0;i < numbers.length;i++){
if(count === 0){
result = numbers[i];
count++;
}else{
if(result === numbers[i]){
count++;
}else{
count--;
}
}
}
let times = numbers.filter(x => x === result).length;
return times > Math.floor(numbers.length >> 1) ? result : 0;
}
只出现一次的数字
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素
var singleNumber = function(nums) {
let num = nums[0];
for(let i = 1;i < nums.length;i++){
num ^= nums[i];
}
return num;
};
比特位计数
给定一个非负整数 num。对于 0 ≤ i ≤ num 范围中的每个数字 i ,计算其二进制数中的 1 的数目并将它们作为数组返回
1. 奇数1的个数等于前一个偶数+1
2. 偶数1的个数等于当前偶数 >> 1 的值
var countBits = function(num) {
let res = [0];
for(let i = 1;i <= num;i++){
if(i & 1){
res[i] = res[i-1] + 1;
}else{
res[i] = res[i >> 1];
}
}
return res;
};
汉明距离
两个整数之间的汉明距离指的是这两个数字对应二进制位不同的位置的数目。
给出两个整数 x 和 y,计算它们之间的汉明距离
1. 亦或求出不同部分
2. 统计
var hammingDistance = function(x, y) {
let ans = x ^ y,count = 0;
while(ans){
if(ans & 1) count++;
ans = ans >> 1;
}
return count;
};
写一个函数,求两个整数之和,要求在函数体内不得使用+、-、*、/四则运算符号
1. ^ 不进位的加法
2. & 判断进位点
3. << 1 进位
function Add(num1, num2) {
return num2 ? Add(num1 ^ num2,(num1 & num2) << 1) : num1;
}
双指针
顾名思义,用两个指针进行查找,提高查找的效率
n数之和
两数之和
var twoSum = function(nums, target) {
if(!nums.length) return [];
let num = nums.slice(0);
nums.sort((x,y) => x-y);
let l = 0,r = nums.length-1;
while(l < r){
if(nums[l] + nums[r] === target) break;
else if(nums[l] + nums[r] < target){
l++;
}else{
r--;
}
}
l = num.indexOf(nums[l]);
r = num.indexOf(nums[r]) === l ? num.indexOf(nums[r],l+1) : num.indexOf(nums[r])
return [l,r];
};
三数之和
var threeSum = function(nums) {
if(nums.length < 3) return [];
nums.sort((x,y) => x-y);
let res = [];
for(let i = 0;i < nums.length;i++){
//如果第一个数大于1就没必要排了
if(nums[i] > 0) return res;
//去重
if(i && nums[i] === nums[i-1]) continue;
let left = i+1,right = nums.length-1;
while(left < right){
if(nums[left] + nums[right] + nums[i] === 0){
res.push([nums[i],nums[left],nums[right]]);
//去重
while(left < right && nums[left] === nums[left+1]){
left++;
}
while(left < right && nums[right] === nums[right-1]){
right--;
}
left++;
right--;
}else if(nums[left] + nums[right] + nums[i] > 0){
right--;
}else{
left++;
}
}
}
return res;
};
最接近的三数之和
//思路与前面基本一致,但需要两个变量,一个更新答案,一个更新最小差值
var threeSumClosest = function(nums, target) {
if(!nums.length) return 0;
let res = Infinity,mins = Infinity;
nums.sort((x,y) => x-y);
for(let i = 0;i < nums.length;i++){
let left = i + 1,right = nums.length-1;
while(left < right){
mins = Math.min(Math.abs(nums[i]+nums[left]+nums[right]-target),mins);
mins === Math.abs(nums[i]+nums[left]+nums[right]-target)
&& (res = nums[i]+nums[left]+nums[right]);
if(nums[i]+nums[left]+nums[right] < target){
left++;
}else if(nums[i]+nums[left]+nums[right] > target){
right--;
}else{
break;
}
}
}
return res;
};
雨水,容器类问题
盛最多水的容器
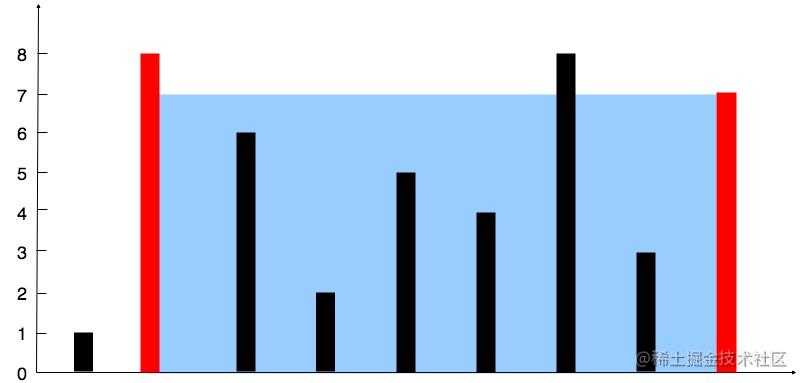
//双指针时刻更新最大值即可,实质上还是枚举
var maxArea = function(height) {
if(!height.length) return 0;
let left = 0,right = height.length-1,res = 0;
while(left < right){
if(height[left] <= height[right]){
let cur = height[left] * (right - left);
res = Math.max(res,cur);
left++;
}else{
let cur = height[right] * (right - left);
res = Math.max(res,cur);
right--;
}
}
return res;
};
接雨水
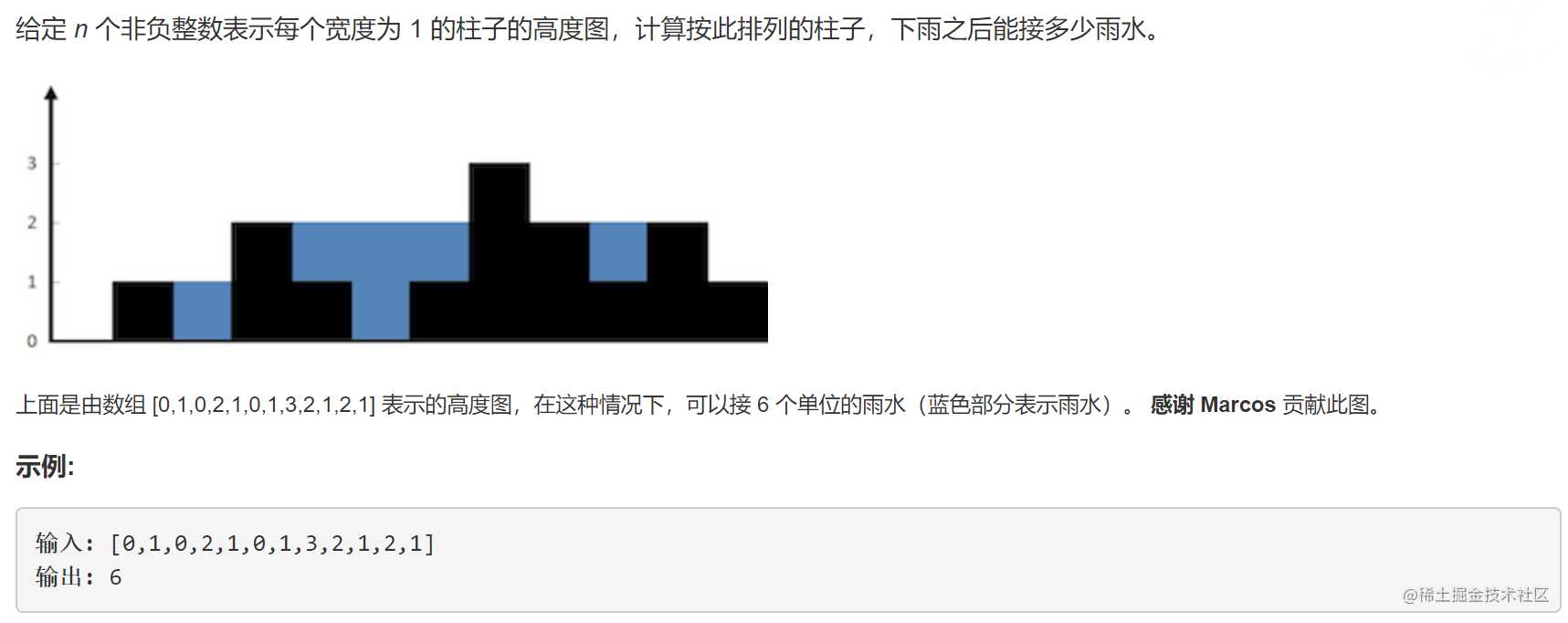
// 比较巧妙的是如何获取每个单元格所能存放的雨水,可以有以下式子简单表示
// 以左边为例:当前柱子存水量 = 最近最高柱子高度(只看左边到当前柱子) - 当前柱子高度
// 右边同理
function trap(arr){
if(!arr.length) return 0;
let left = 0,right = arr.length-1,leftHeight = 0,rightHeight = 0,res = 0;
while(left < right){
if(arr[left] < arr[right]){
leftHeight = Math.max(arr[left],leftHeight);
res += leftHeight - arr[left];
left++;
}else{
rightHeight = Math.max(arr[right],rightHeight);
res += rightHeight - arr[right];
right--;
}
}
return res;
}
长度最小的子数组
给定一个含有 n 个正整数的数组和一个正整数 s ,找出该数组中满足其和 ≥ s 的长度最小的连续子数组,并返回其长度。如果不存在符合条件的连续子数组,返回 0。
// 滑动窗口的解法
// 每次将右指针对应的数添加到临时num中
// 查看是否满足题意,满足则作为一个可行解与len作比较,同时移动左指针
// 移动右指针到下一个位置
var minSubArrayLen = function(s, nums) {
let left = 0, right = 0, len = Infinity, num = 0;
while(right < nums.length) {
num += nums[right];
while(num >= s) {
len = Math.min(len, right - left + 1);
num -= nums[left];
left++;
}
right++;
}
return len === Infinity ? 0 : len;
};
链表类
删除链表的倒数第n个节点
var removeNthFromEnd = function(head, n) {
if(!head) return null;
let fast = head,slow = head,pre = head,p1 = head,len = 0;
while(p1){
len++;
p1 = p1.next;
}
//注意头节点删除的情况
if(len === n) return head.next;
while(n--){
fast = fast.next;
}
while(fast){
fast = fast.next;
pre = slow;
slow = slow.next;
}
pre.next = slow.next;
return head;
};
请判断一个链表是否为回文链表
1. 将前半部分链表反转
2. 判断前后两部分链表是否相等
var isPalindrome = function(head) {
if(!head) return true;
let pre = null,temp,fast = head,slow = head;
while(fast && fast.next){
fast = fast.next.next;
// 反转链表
temp = slow;
slow = slow.next;
temp.next = pre;
pre = temp;
}
if(fast) slow = slow.next;
while(pre && slow){
if(pre.val !== slow.val) return false;
pre = pre.next;
slow = slow.next;
}
return true;
};
给定一个链表,判断链表中是否有环
var hasCycle = function(head) {
if(!head || !head.next || !head.next.next) return false;
let fast = head.next.next,slow = head.next;
while(fast !== slow){
if(fast === null || fast.next === null) return false;
fast = fast.next.next;
slow = slow.next;
}
return true;
};
输入一个链表,输出该链表中倒数第k个结点。
function FindKthToTail(head, k) {
// write code here
if(head === null || k === 0) return null;
let fast = head,slow = head;
while(k--){
if(fast === null) return null;
fast = fast.next;
}
while(fast){
fast = fast.next;
slow = slow.next;
}
return slow;
}
输入两个单调递增的链表,输出两个链表合成后的链表,当然我们需要合成后的链表满足单调不减规则。
//注意与拷贝链表区分
function Merge(pHead1, pHead2) {
if(pHead1 === null){
return pHead2;
}else if(pHead2 === null){
return pHead1;
}
if(pHead1.val < pHead2.val){
pHead1.next = Merge(pHead1.next,pHead2);
return pHead1;
}else{
pHead2.next = Merge(pHead2.next,pHead1);
return pHead2;
}
}
输入两个链表,找出它们的第一个公共结点
function FindFirstCommonNode(pHead1, pHead2) {
// write code here
let p1 = pHead1,p2 = pHead2;
while (p1 !== p2){
p1 = p1 === null ? pHead2 : p1.next;
p2 = p2 === null ? pHead1 : p2.next;
}
return p1;
}
找出环形链表入环位置
var detectCycle = function(head) {
if(!head || !head.next) return null;
let fast = head.next.next,slow = head.next,p1 = head;
while(fast !== null && fast !== slow){
if(fast.next) fast = fast.next.next;
else fast = null;
slow = slow.next;
}
if(fast === null) return null;
else{
while(p1 !== slow){
p1 = p1.next;
slow = slow.next;
}
return slow;
}
};
字符串类
验证回文串
var isPalindrome = function(s) {
let reg = /[a-z]|[0-9]/;
s = s.split('').map(x => x.toLowerCase()).filter((x) => reg.test(x)).join('');
let head = 0;
let tail = s.length-1;
while(head <= tail){
if(s[head] !== s[tail]) return false;
head++;
tail--;
}
return true;
};
矩阵
顺时针打印矩阵
输入一个矩阵,按照从外向里以顺时针的顺序依次打印出每一个数字
// 例如,如果输入如下4 X 4矩阵: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 则依次打印出数字1,2,3,4,8,12,16,15,14,13,9,5,6,7,11,10.
旋转魔方法,每次打印第一列,然后将矩阵逆时针旋转
function rotate(arr){
if(!arr.length) return [];
let newArr = [];
for(let i = 0;i < arr[0].length;i++){
let temp = [];
for(let j = 0;j < arr.length;j++){
temp.push(arr[j][arr[0].length-1-i]);
}
newArr.push(temp);
}
return newArr;
}
function printMatrix(matrix) {
if(!matrix.length) return [];
let ans = [];
while(matrix.length){
for(let i = 0;i < matrix[0].length;i++){
ans.push(matrix[0][i])
}
matrix.splice(0,1);
matrix = rotate(matrix);
}
return ans;
}
旋转图像
给定一个 n × n 的二维矩阵表示一个图像。
将图像顺时针旋转 90 度
var rotate = function(matrix) {
if(!matrix.length) return [];
let left = 0,right = matrix.length-1;
while(right-left > 0){
[matrix[left],matrix[right]] = [matrix[right],matrix[left]];
left++;
right--;
}
for(let i = 0;i < matrix.length;i++){
for(let j = i+1;j < matrix[i].length;j++){
[matrix[i][j],matrix[j][i]] = [matrix[j][i],matrix[i][j]];
}
}
return matrix;
};
螺旋矩阵 II
给定一个正整数 n,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的正方形矩阵
//基本就是模拟这个过程,要注意转弯的边界条件
var generateMatrix = function(n) {
let rows = n-1,cols = n-1,col = 0,row = 0,iter = 1,x_dire = 1,y_dire = 1,cur_dire = 1,res = [];
for(let i = 0;i < n;i++) res.push([]);
while(iter <= n ** 2) {
if (cur_dire === 1 && res[row][col] === undefined) {
res[row][col] = iter;
iter++;
if (x_dire === 1) {
if (col < cols) {
col++;
} else {
cur_dire = -1;
x_dire = -x_dire;
if (y_dire === 1) row++;
else row--;
}
} else {
if (col > 0) {
col--;
} else {
cur_dire = -1;
x_dire = -x_dire;
if (y_dire === 1) row++;
else row--;
}
}
}else if (cur_dire === 1 && res[row][col]) {
if (y_dire === 1) row++;
else row--;
x_dire = -x_dire;
cur_dire = -1;
if (x_dire === 1) col++;
else col--;
}else if (cur_dire === -1 && res[row][col] === undefined) {
res[row][col] = iter;
iter++;
if (y_dire === 1) {
if (row < rows) {
row++;
} else {
cur_dire = 1;
y_dire = -y_dire;
if (x_dire === 1) col++;
else col--;
}
} else {
if (row >= 0) {
row--;
} else {
cur_dire = 1;
y_dire = -y_dire;
if (x_dire === 1) col++;
else col--;
}
}
} else if(cur_dire === -1 && res[row][col]) {
if (x_dire === 1) col++;
else col--;
y_dire = -y_dire;
cur_dire = 1;
if (y_dire === 1) row++;
else row--;
}
}
return res;
};
矩阵置零
给定一个 m x n 的矩阵,如果一个元素为 0,则将其所在行和列的所有元素都设为 0。请使用**原地**算法
//利用了js的特性,-0和0的不相等
//将0所在行列中非0元素置为-0
var setZeroes = function(matrix) {
for(let i = 0;i < matrix.length;i++){
for(let j = 0;j < matrix[i].length;j++){
if(Object.is(matrix[i][j],0)){
for(let k = 0;k < matrix.length;k++){
if(k !== i && Object.is(matrix[k][j],0)) continue;
else matrix[k][j] = -0
}
for(let k = 0;k < matrix[i].length;k++){
if(k !== j && Object.is(matrix[i][k],0)) continue;
else matrix[i][k] = -0
}
}
}
}
return matrix;
};
杨辉三角
//入坑题
function print(n) {
let arr = [],n1 = n;
while(n1--){
arr.push([]);
}
for(let i = 0;i < n;i++){
for(let j = 0;j <= i;j++){
if(j === 0 || j === i) arr[i][j] = 1;
else{
arr[i][j] = arr[i-1][j-1]+arr[i-1][j];
}
}
}
arr.forEach(x => console.log(x.toString().replace(/,/g,' ')));
}
二叉树
遍历系列
二叉树的前中后序遍历(递归和非递归)
//递归
function pre(root){
if(!root) return root;
console.log(root.val);
pre(root.left);
pre(root.right);
}
function mid(root){
if(!root) return root;
mid(root.left);
console.log(root.val);
mid(root.right);
}
function next(root){
if(!root) return root;
next(root.right);
next(root.left);
console.log(root.val);
}
//非递归
//前序
//用栈进行模拟
//每次将栈顶元素添加到结果中,然后将栈顶元素的左右非空子树入栈(注意右子树先入栈,后弹出)
//直到栈为空跳出循环
function pre(root){
if(root === null) return root;
let res = [],stack = [];
stack.push(root);
while (stack.length){
let node = stack.pop();
res.push(node.val);
node.right && stack.push(node.right);
node.left && stack.push(node.left);
}
return res;
}
//中序
//对栈顶元素深度遍历左子树入栈,然后将栈顶添加到结果中,然后访问当前子节点的右子树,依次循环
function mid(root){
if(root === null) return root;
let res = [],stack = [];
stack.push(root);
while (stack.length){
while(root !== null){
stack.push(root);
root = root.left;
}
let node = stack.pop()
res.push(node.val);
root = node.right;
}
//根节点添加了两次
return res.slice(0,res.length-1);
}
//后序
//与前序相似,但生成顺序为根右左,最后将res反序
function next(root){
if(root === null) return root;
let res = [],stack = [];
stack.push(root);
while (stack.length){
let node = stack.pop();
res.push(node.val);
node.left && stack.push(node.left);
node.right && stack.push(node.right);
}
return res.reverse();
}
层次遍历
var levelOrder = function(root) {
if(!root) return [];
let nodes = [],queue = [root],path=[];
let cur = 1,next = 0;
while(queue.length){
let node = queue.shift();
path.push(node.val);
node.left && queue.push(node.left) && next++;
node.right && queue.push(node.right) && next++;
cur--;
if(!cur){
nodes.push(path);
path = [];
cur = next;
next = 0;
}
}
return nodes;
};
遍历变种
二叉树的锯齿形层次遍历
给定一个二叉树,返回其节点值的锯齿形层次遍历。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。
var zigzagLevelOrder = function(pRoot) {
if(!pRoot) {
return []
}
var queue = [], res = [], temp = [],
node, level = 0, toBePrinted = 1, isEven = true;
queue.push(pRoot);
while(queue.length) {
node = queue.shift();
// 判断当前行为奇数行还是偶数行
if(isEven) {
temp.push(node.val);
} else {
temp.unshift(node.val);
}
// 计算每一行的元素个数
if(node.left) {
queue.push(node.left);
level++;
}
if(node.right) {
queue.push(node.right);
level++;
}
toBePrinted--;
// 判断当前行是否全部输出完毕
if(toBePrinted === 0) {
res.push(temp);
temp = [];
toBePrinted = level;
level = 0;
isEven = !isEven;
}
}
return res;
};
从上到下按层打印二叉树,同一层结点从左至右输出。每一层输出一行。
//相比bfs,需要增加两个变量,一个存当前层次的还有多少节点需要打印,一个存储下一层次有多少个节点(每次队列push时进行++)
function Print(pRoot) {
let nodes = [],queue = [pRoot],path=[];
let cur = 1,next = 0;
while(queue.length){
let node = queue.shift();
path.push(node.val);
node.left && queue.push(node.left) && next++;
node.right && queue.push(node.right) && next++;
cur--;
if(!cur){
nodes.push(path);
path = [];
cur = next;
next = 0;
}
}
return nodes;
}
根据已知二叉树,求某值
求二叉树的深度
function TreeDepth(pRoot) {
if(pRoot === null) return 0;
let left = TreeDepth(pRoot.left);
let right = TreeDepth(pRoot.right);
return Math.max(left,right) + 1;
}
二叉搜索树中第K小的元素
var kthSmallest = function(root, k) {
let res;
function midOrder(root){
if(!root) return root;
midOrder(root.left);
if(k === 0) return res;
else{
res = root.val;
k--;
}
midOrder(root.right);
}
midOrder(root);
return res;
};
二叉树最近公共祖先
(1)深度优先查找,查到两节点任意一个返回
(2)当两个节点都找到时返回root,否则返回null
var lowestCommonAncestor = function(root, p, q) {
if(!root) return null;
if(root === p || root === q) return root;
let left = lowestCommonAncestor(root.left,p,q);
let right = lowestCommonAncestor(root.right,p,q);
if(!left) return right;
if(!right) return left;
if(left && right) return root;
return null;
};
给定一棵二叉树,你需要计算它的直径长度。
一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。
易错点是直径可能不经过根节点
用max保存最大值,
当每个节点作为根节点时,与max比较进行更新
var diameterOfBinaryTree = function(root) {
let max = 0;
function dfs(root){
if(!root) return 0;
let l = dfs(root.left);
let r = dfs(root.right);
max = Math.max(max,l+r);
return Math.max(l,r)+1;
}
dfs(root);
return max;
};
求根到叶子节点数字之和
给定一个二叉树,它的每个结点都存放一个 0-9 的数字,每条从根到叶子节点的路径都代表一个数字。
例如,从根到叶子节点路径 1->2->3 代表数字 123。
计算从根到叶子节点生成的所有数字之和。
说明: 叶子节点是指没有子节点的节点。
// 简单的dfs
var sumNumbers = function(root) {
let res = 0;
function dfs(root,temp) {
if(!root) return;
temp += root.val;
if((!root.left) && (!root.right)) res += Number(temp);
dfs(root.left,temp);
dfs(root.right,temp);
}
dfs(root,'');
return res;
};
一些特殊的二叉树(判断和构建)
判断二叉树是否是对称二叉树
function mirrors(root) {
if(root === null) return root;
[root.left,root.right] = [root.right,root.left];
mirrors(root.left);
mirrors(root.right);
}
var isSymmetric = function(root) {
let mirror = JSON.parse(JSON.stringify(root));
mirrors(mirror);
if(JSON.stringify(mirror) === JSON.stringify(root)){
return true;
}else{
return false;
}
};
验证二叉搜索树
给定一个二叉树,判断其是否是一个有效的二叉搜索树。
let pre = -Infinity;
var isValidBST = function(root) {
if(!root) return true;
let left = isValidBST(root.left);
if(root.val <= pre || !left) return false;
pre = root.val;
return isValidBST(root.right);
};
从前序与中序遍历序列构造二叉树
var buildTree = function(preorder, inorder) {
if(!preorder.length || !inorder.length) return null;
let root = new TreeNode(preorder[0]);
let key = 0;
for(let i = 0;i < inorder.length;i++){
if(inorder[i] === preorder[0]){
key = i;
break;
}
}
root.left = buildTree(preorder.slice(1,key+1),inorder.slice(0,key));
root.right = buildTree(preorder.slice(key+1),inorder.slice(key+1));
return root;
};
翻转二叉树
var invertTree = function(root) {
if(root === null) return root;
[root.left,root.right] = [root.right,root.left];
invertTree(root.left);
invertTree(root.right);
return root;
};
把二叉搜索树转换为累加树
var convertBST = function(root) {
let cur = 0;
re = function(root){
if(!root) return root;
re(root.right);
root.val += cur;
cur = root.val;
re(root.left);
return root;
}
return re(root);
};
合并二叉树
var mergeTrees = function(t1, t2) {
if(t1 && t2){
t1.val += t2.val;
t1.left = mergeTrees(t1.left,t2.left);
t1.right = mergeTrees(t1.right,t2.right);
}
return t1 || t2;
};
输入两棵二叉树A,B,判断B是不是A的子结构
(ps:我们约定空树不是任意一个树的子结构)
function TreeNode(x) {
this.val = x;
this.left = null;
this.right = null;
}
//判断是否为子结构跟先序遍历类似
function isSubtree(root1,root2) {
if(!root2) return true;
if(!root1) return false;
if(root1.val !== root2.val) return false;
return isSubtree(root1.left,root2.left) && isSubtree(root1.right,root2.right);
}
//从根节点开始递归判断是否含有子结构
function HasSubtree(pRoot1, pRoot2) {
if(!pRoot1 || !pRoot2) return false;
return (
isSubtree(pRoot1,pRoot2)
|| HasSubtree(pRoot1.left,pRoot2)
|| HasSubtree(pRoot1.right,pRoot2)
)
}
操作给定的二叉树,将其变换为源二叉树的镜像
function Mirror(root) {
if(root === null) return root;
[root.left,root.right] = [root.right,root.left];
Mirror(root.left);
Mirror(root.right);
return root;
}
输入一棵二叉树,判断该二叉树是否是平衡二叉树
1. 比较两颗子树的高度,两边都取最大深度
2. 查看两颗子树高度差是否相差为1
3. 如果大于1,那么将其标记为-1(表示不是AVL树),然后每次递归时先判断该节点的子树是否时AVL树
function IsBalanced_Solution(pRoot) {
return orderTree(pRoot) !== -1;
}
function orderTree(root) {
if(!root) return 0;
let left = orderTree(root.left);
let right = orderTree(root.right);
if(left === -1 || right === -1 || Math.abs(left-right) > 1) return -1;
return Math.max(left,right)+1;
}
求二叉树的一些路径
路径总和 III
给定一个二叉树,它的每个结点都存放着一个整数值。
找出路径和等于给定数值的路径总数。
路径不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
二叉树不超过1000个节点,且节点数值范围是 [-1000000,1000000] 的整数。
function dfs(cur,sum,root,path,res){
cur += root.val;
path.push(root.val);
if(cur === sum && !root.left && !root.right){
res.push(path.slice(0));
}
root.left && dfs(cur,sum,root.left,path,res);
root.right && dfs(cur,sum,root.right,path,res);
path.pop();
}
var pathSum = function(root, sum) {
if(!root) return [];
let res = [],path = [],cur = 0;
dfs(cur,sum,root,path,res);
return res;
};
二叉树中和为某一值的路径
输入一棵二叉树和一个整数,打印出二叉树中节点值的和为输入整数的所有路径。从树的根节点开始往下一直到叶节点所经过的节点形成一条路径。
// 路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。(注意: 在返回值的list中,数组长度大的数组靠前)
1. dfs + 回溯
2. 深度搜索路径,将路径中的每个节点值相加,路径存入缓存,直到遍历到最深处
3. 比较当前值是否为目标值,如果是将缓存的路径加入结果数组,如果不是则回退到上一个节点
function dfs(root,expectNumber,cur,path,result) {
cur += root.val;
path.push(root);
if(cur === expectNumber && root.left === null && root.right === null){
result.push(path.slice(0));
}
root.left && dfs(root.left,expectNumber,cur,path,result);
root.right && dfs(root.right,expectNumber,cur,path,result);
//重要
path.pop();
}
function FindPath(root, expectNumber) {
let result = [],path = [],cur = 0;
if(!root) return result;
dfs(root,expectNumber,cur,path,result);
return result;
}
二叉树中的最大路径和
给定一个非空二叉树,返回其最大路径和。
本题中,路径被定义为一条从树中任意节点出发,达到任意节点的序列。该路径至少包含一个节点,且不一定经过根节点。
var maxPathSum = function(root) {
let max = -Infinity;
function dfs(root){
if(!root) return 0;
let l = Math.max(dfs(root.left),0);
let r = Math.max(dfs(root.right),0);
max = Math.max(max,l + r + root.val);
return Math.max(l,r)+root.val;
}
dfs(root);
return max;
};
其他
不同的二叉索引树的个数
卡塔兰数
dp[0] = 1
dp[i] = dp[i-1] * (4 * i + 2) / (i + 2);
var numTrees = function(n) {
if(!n) return 0;
let dp = [1];
for(let i = 1;i < n;i++){
dp[i] = dp[i-1] * (4 * i + 2) /(i + 2);
}
return dp[n-1];
};
根据js的依赖关系树tree,输出合理的打包顺序的数组(阿里面试题)
function resolve(tree){
let len = tree.require.length,queue = [];
for(let i = 0;i < len;i++){
queue.push([]);
}
tree = flatten(tree);
let head = tree.name;
for(let key in tree){
let k = Number(key.slice(8,9));
Object.keys(tree[key]).length && queue[k].push(tree[key])
}
let res = [];
for(let i = queue.length-1;i >= 0;i--){
for(let j = queue[i].length-1;j >= 0;j--){
res.indexOf(queue[i][j]) === -1 && res.push(queue[i][j]);
}
}
return res;
}
function flatten(input) {
let res = {};
let re = function(obj,key){
if(obj instanceof Object && !(obj instanceof Array)){
let empty = true;
for(let i in obj){
re(obj[i],key ? `${key}.${i}` : i)
}
if(empty && key){
res[key] = {};
}
}else if(obj instanceof Array){
if(obj.length){
for(let i = 0;i < obj.length;i++){
re(obj[i],key ? `${key}[${i}]` : i)
}
}else{
res[key] = [];
}
}else{
if(obj !== undefined && obj !== null){
res[key] = obj;
}
}
};
re(input,'');
return res;
}
var tree1 = {
name: 'main.js',
require: [{
name: 'A.js'
}, {
name: 'B.js'
}] }
var tree2 = {
name: 'page.js',
require: [{
name: 'A.js',
require: [{
name: 'B.js',
require: [{
name: 'C.js'
}]
}]},
{
name: 'D.js',
require: [{
name: 'C.js'
}, {
name: 'E.js'
}]
}] }
resolve(tree1) // ['A.js', 'B.js', 'main.js']
resolve(tree2) // ['C.js', 'E.js', 'D.js', 'B.js', 'A.js', 'page.js']
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。假设输入的数组的任意两个数字都互不相同。
1. 后序遍历的最后一个节点为根节点
2. 二叉索引树右子树大于根节点,左子树小于根节点,所以可以用根节点将树分为两颗子树
3. 二叉索引树的子树也是二叉索引树,所以分别对子树进行判断,直到遍历到最后一个节点
var verifyPostorder = function(postorder) {
if(!postorder.length) return true;
let tail = postorder.pop();
let key = postorder.length;
for(let i = 0;i < postorder.length;i++){
if(postorder[i] > tail){
key = i;
break;
}
}
for(let i = key+1;i < postorder.length;i++){
if(postorder[i] < tail){
return false;
}
}
return verifyPostorder(postorder.slice(0));
};
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的双向链表
var treeToDoublyList = function(root) {
if(!root) return null;
let head = null,tail = null,pre = null;
function dfs(root){
if(!root) return null;
dfs(root.left);
//第一个节点作为头节点
if(!pre) head = root;
//将上一个节点的后继指针指向当前节点
else pre.right = root;
//将当前指针的前驱指针指向上一个节点
root.left = pre;
//更新上一个节点
pre = root;
//更新尾部节点
tail = root;
dfs(root.right);
}
dfs(root);
//首尾连接
head.left = tail;
tail.right = head;
return head;
};
二叉树展开为链表
前序遍历,将右子树放到左子树最右叶子节点的后面,将左子树放到右子树上,左子树置空
var flatten = function(root) {
function dfs(root){
if(!root) return;
dfs(root.left);
dfs(root.right);
let pre = root.left;
if(pre){
//获取左子树最右叶子节点
while(pre.right){
pre = pre.right;
}
//将右子树放在左子树最右右子节点后面
pre.right = root.right;
//将新构建的左子树放在右子树上
root.right = root.left;
//左子树置空
root.left = null;
}
}
dfs(root);
return root;
};
哈希表
面试中能用hashmap解的题往往有更优的解法,但hashmap不失为一种最容易想到和容易书写的解法
每日温度
根据每日 气温 列表,请重新生成一个列表,对应位置的输出是需要再等待多久温度才会升高超过该日的天数。如果之后都不会升高,请在该位置用 0 来代替。
例如,给定一个列表 temperatures = [73, 74, 75, 71, 69, 72, 76, 73],你的输出应该是 [1, 1, 4, 2, 1, 1, 0, 0]。
提示:气温 列表长度的范围是 [1, 30000]。每个气温的值的均为华氏度,都是在 [30, 100] 范围内的整数。
var dailyTemperatures = function(T) {
let res = [],len = T.length;
while(len--){
res.push(0);
}
for(let i = 0;i < T.length;i++){
for(let j = i+1;j < T.length;j++){
if(T[j] <= T[i]){
res[i]++;
if(j === T.length-1) res[i] = 0;
}else{
res[i]++;
break;
}
}
}
return res;
};
字母异位词分组
给定一个字符串数组,将字母异位词组合在一起。字母异位词指字母相同,但排列不同的字符串
var groupAnagrams = function(strs) {
if(!strs.length) return [];
let str = strs.slice(0),res = [];
strs = strs.map(x => x.split('').sort().join(''));
let map = new Map();
for(let i = 0;i < strs.length;i++){
map.hasOwnProperty(strs[i]) ? map[strs[i]].push(str[i]) : (map[strs[i]] = [str[i]]);
}
for(let key in map){
res.push(map[key]);
}
return res;
};
和为K的子数组
给定一个整数数组和一个整数 **k,**你需要找到该数组中和为 k 的连续的子数组的个数
var subarraySum = function(nums, k) {
if(!nums.length) return 0;
let res = 0;
for(let i = 0;i < nums.length;i++){
let cur = 0;
for(let j = i;j < nums.length;j++){
cur += nums[j];
if(cur === k) res++;
}
}
return res;
};
前 K 个高频元素
给定一个非空的整数数组,返回其中出现频率前 k 高的元素
var topKFrequent = function(nums, k) {
if(!nums.length) return [];
let map = new Map();
for(let i = 0;i < nums.length;i++){
map.has(nums[i]) ? map.set(nums[i],map.get(nums[i])+1) : map.set(nums[i],1);
}
let values = [],res = [];
for(let [k,i] of map){
values.push(i);
}
values.sort((x,y) => y-x);
values = values.slice(0,k);
for(let [k,i] of map){
if(values.indexOf(i) !== -1){
res.push(k);
}
}
return res;
};
在一个长度为n的数组里的所有数字都在0到n-1的范围内。 数组中某些数字是重复的,但不知道有几个数字是重复的。也不知道每个数字重复几次。
// 请找出数组中任意一个重复的数字。 例如,如果输入长度为7的数组{2,3,1,0,2,5,3},那么对应的输出是第一个重复的数字2。
function duplicate(numbers, duplication) {
let map = new Map();
for(let i = 0;i < numbers.length;i++){
map.has(numbers[i]) ? map.set(numbers[i],map.get(numbers[i]) + 1) : map.set(numbers[i],1);
if(map.get(numbers[i]) > 1){
duplication[0] = numbers[i];
return true;
}
}
return false;
}
在一个字符串(0<=字符串长度<=10000,全部由字母组成)中找到第一个只出现一次的字符,并返回它的位置
// 如果没有则返回 -1(需要区分大小写).
function FirstNotRepeatingChar(str) {
let map = new Map();
for(let key of str){
map.has(key) ? map.set(key,map.get(key)+1) : map.set(key,1);
}
for(let [key,value] of map){
if(value === 1) return str.indexOf(key);
}
return -1;
}
计数质数
统计所有小于非负整数 n 的质数的数量

给出要筛选数值的范围n,找出sqrt(n)以内的素数,先用 2 去筛,即把 2 留下,把 2 的倍数剔除掉;再用下一个素数,也就是 3 筛,把 3 留下,把 3 的倍数剔除掉;接下去用下一个素数 5 筛,把 5 留下,把 5 的倍数剔除掉;不断重复下去
var countPrimes = function(n) {
let count = 0;
let signs = new Uint8Array(n);
for (let i = 2; i < n; i++) {
// 如果是素数
if (!signs[i - 1]) {
count++;
// 去除当前素数的n次项
for (let j = i * i; j <= n; j += i) {
signs[j - 1] = true;
}
}
}
return count;
};
把只包含质因子2、3和5的数称作丑数
返回第k个丑数
//例如6、8都是丑数,但14不是,因为它包含质因子7。 习惯上我们把1当做是第一个丑数。求按从小到大的顺序的第N个丑数。
1. 0-6都是丑数,返回其值即可
2. 使用t1-t3表示2,3,5公因子的个数,每次取最小的公因子值,初值为1
function GetUglyNumber_Solution(index) {
if(index < 7) return index;
let res = [1];
let t2 = 0,t3 = 0,t5 = 0;
for(let i = 1;i < index;i++){
res[i] = Math.min(res[t2]*2,res[t3]*3,res[t5]*5);
res[i] === res[t2]*2 && t2++;
res[i] === res[t3]*3 && t3++;
res[i] === res[t5]*5 && t5++;
}
return res[index-1]
}
无重复字符的最长子串
给定一个字符串,请你找出其中不含有重复字符的 最长子串 的长度。
var lengthOfLongestSubstring = function(s) {
if(!s.length) return '';
let sub = '',res = '';
for(let i = 0;i < s.length;i++){
if(sub === ''){
sub += s[i];
if(i === s.length-1 && res.length < sub.length) res = sub;
}else{
if(sub.indexOf(s[i]) === -1){
sub += s[i];
if(i === s.length-1 && res.length < sub.length) res = sub;
}else{
if(sub.length > res.length) res = sub;
sub = sub.substr(sub.indexOf(s[i])+1) + s[i];
}
}
}
return res.length;
};
栈和队列
栈满足先进后出,队列满足先进先出
用两个栈来实现一个队列,完成队列的Push和Pop操作。 队列中的元素为int类型
1. 用出入栈进行模拟
2. 进队列全部添加到入栈中
3. 出队列检查出栈是否为空,不为空则将栈顶元素出栈;为空则先将入栈中的所有元素压入出栈
let in_stack = [],out_stack = [];
function push(value) {
in_stack.push(value);
}
function pop() {
if(!out_stack.length){
while(in_stack.length > 0){
out_stack.push(in_stack.pop())
}
}else{
return out_stack.pop();
}
}
定义栈的数据结构,请在该类型中实现一个能够得到栈中所含最小元素的min函数(时间复杂度应为O(1)
1. 使用辅助栈存最小值
2. 入栈时检查元素是否为最小值,若是则压入主栈和辅助栈
3. 出栈时检查主栈栈顶元素是否与辅助栈一致,若是则一起弹出
// 注意:保证测试中不会当栈为空的时候,对栈调用pop()或者min()或者top()方法。
let stack1 = [],stack2 = [];
function push(value) {
if(value <= Math.min(...stack1) || stack1.length === 0){
stack1.unshift(value);
stack2.unshift(value);
}else{
stack1.unshift(value)
}
}
function pop() {
if(stack1.length > 0) {
if (stack1[0] === stack2[0]) {
stack1.shift();
stack2.shift();
} else {
stack1.shift();
}
}
}
function top() {
if(stack1.length > 0) {
return stack1[0];
}
}
function min() {
if(stack2.length > 0) {
return stack2[0];
}
}
滑动窗口的最大值
给定一个数组 nums 和滑动窗口的大小 k,请找出所有滑动窗口里的最大值。
1. 维护一个单调的双向队列
2. 新增元素与队尾元素比较,比队尾小直接添加,比队尾大,弹出队尾,直到找到该元素合适的位置
3. 每次将双向队列中队首元素添加到结果中
var maxSlidingWindow = function(nums, k) {
if (k === 0) return [];
const length = nums.length;
if (length === 0) return [];
const deque = [];
for (let i = 0; i < k; ++i) {
cleanDeque(deque, nums, i, k);
deque.push(i);
}
const res = [];
res.push(nums[deque[0]]);
for (let i = k; i < length; ++i) {
cleanDeque(deque, nums, i, k);
deque.push(i);
res.push(nums[deque[0]]);
}
return res;
};
function cleanDeque(queue, arr, cur, k) {
// 如果双向队列中,包含不是滑动窗口内的数,直接出队
if (queue.length && cur >= k + queue[0]) {
queue.shift();
}
while (queue.length && arr[idx] > nums[queue[queue.length - 1]]) {
queue.pop();
}
}
有效的括号
给定一个只包括 ‘(‘,’)’,'{‘,’}’,'[‘,’]’ 的字符串,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。 左括号必须以正确的顺序闭合。
左括号入栈,右括号与栈顶比较是否匹配,匹配弹出栈顶,不匹配return false
查看栈是否为空
var isValid = function(s) {
if(!s.length) return true;
let stack = [];
for(let i = 0;i < s.length;i++){
if(s[i] === '(' || s[i] === '{' || s[i] === '['){
stack.unshift(s[i]);
}else{
if(s[i] === ')'){
if(stack[0] === '(') stack.shift();
else{
return false;
}
}else if(s[i] === ']'){
if(stack[0] === '[') stack.shift();
else{
return false;
}
}else if(s[i] === '}'){
if(stack[0] === '{') stack.shift();
else{
return false;
}
}
}
}
return stack.length === 0;
};
字符串解码
给定一个经过编码的字符串,返回它解码后的字符串。
编码规则为: k[encoded_string],表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。
你可以认为输入字符串总是有效的;输入字符串中没有额外的空格,且输入的方括号总是符合格式要求的。
此外,你可以认为原始数据不包含数字,所有的数字只表示重复的次数 k ,例如不会出现像 3a 或 2[4] 的输入。
var decodeString = function(s) {
// 用两个栈来存放当前状态,前者是重复次数,后者是累积字符串
let repetStack=[],resStack=[];
//拼接字符串
let resStr = "";
//表示重复次数
let repet = 0;
// 遍历s
for(let i=0;i<s.length;i++){
let cur = s.charAt(i);
if(cur == '['){
//双双压入栈中,保存当前状态
repetStack.push(repet);
resStack.push(resStr);
//置空,准备下面的累积
repet = 0;
resStr = "";
}else if(cur == ']'){
// 取出当前重复次数栈中的值,也就是当前字符串的重复次数
let count = repetStack.pop();
// 根据重复次数生成重复字符串,赋值给temp,和resStr拼接
let temp = "";
for(let i = 0;i<count;i++){
temp += resStr;
}
// 和前面已经求得的字符串进行拼接
resStr = resStack.pop() + temp;
}else if(cur>='0' && cur<='9'){
// repet累积
repet = repet*10 + (cur-'0');
}else{
//字符累积
resStr += cur;
}
}
return resStr;
};
根据身高重建队列
假设有打乱顺序的一群人站成一个队列。 每个人由一个整数对(h, k)表示,其中h是这个人的身高,k是排在这个人前面且身高大于或等于h的人数。 编写一个算法来重建这个队列。
1. 按升高降序,身高相同的按人数升序排列
2. 将队列的每个元素按序插入到索引位置
var reconstructQueue = function(people) {
if(!people) return [];
people.sort((x,y)=>{
return x[0] === y[0] ? x[1]-y[1] : y[0] - x[0];
});
let res = [];
for(let i = 0;i < people.length;i++){
res.splice(people[i][1],0,people[i]);
}
return res;
};
中缀表达式转后缀
//数字直接添加到result
//栈空,运算符直接入栈
//遇到左括号直接入栈,遇到右括号栈顶元素添加到result中然后弹栈,依次循环直到遇到左括号,然后将左括号弹栈
//遇到运算符,判断运算符与栈顶元素的优先级,将所有优先级大于等于该运算符的栈顶弹栈,然后入栈该运算符
//将栈中剩余的字符添加到result中
function toPoland(str){
let stack = [],result = '';
for(let i = 0;i < str.length;i++){
if(!Object.is(Number(str[i]),NaN)){
result += str[i];
}else if(stack.length === 0 && Object.is(Number(str[i]),NaN)){
result += ' ';
stack.push(str[i]);
}else if(str[i] === '('){
stack.push(str[i])
}else if(str[i] === ')'){
result += ' ';
while(stack[stack.length-1] !== '('){
result += stack.pop();
}
stack.pop();
}else if(str[i] === '*' || str[i] === '/'){
while(stack[stack.length-1] === '*' || stack[stack.length-1] === '/'){
result += ' ' + stack.pop();
}
result += ' ';
stack.push(str[i]);
}else if(str[i] === '+' || str[i] === '-'){
while(stack[stack.length-1] === '*' || stack[stack.length-1] === '/' || stack[stack.length-1] === '+' || stack[stack.length-1] === '-'){
result += ' ' + stack.pop();
}
result += ' ';
stack.push(str[i]);
}
}
while(stack.length){
result += ' ' + stack.pop();
}
return result;
}
计算后缀表达式
1. 数字入栈
2. 运算符,栈顶作为右操作数,次栈顶作为左操作数
3. 将运算结果入栈
4. 栈最后一个值即为结果
function CalcRPN(str) {
let stack = [];
let num = '';
for(let i = 0;i < str.length;i++){
if(str[i] === ' '){
if(num !== '') stack.push(Number(num));
num = '';
}else if(!Object.is(Number(str[i]),NaN)){
num += str[i];
}else if(str[i] === '+'){
let right = stack.pop();
let left = stack.pop();
stack.push(left + right);
}else if(str[i] === '-'){
let right = stack.pop();
let left = stack.pop();
stack.push(left - right);
}else if(str[i] === '*'){
let right = stack.pop();
let left = stack.pop();
stack.push(left * right);
}else if(str[i] === '/'){
let right = stack.pop();
let left = stack.pop();
stack.push(left / right);
}
}
return stack.pop();
}
输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。
1. 模拟出栈的过程
2. 变量push栈,每次将一个元素压入辅助栈
3. 判断辅助栈是否为空的同时,pop栈的栈顶是否与辅助栈栈顶元素相同,如果都满足则两者出栈
4. 最后判断辅助栈是否为空
// 例如序列1,2,3,4,5是某栈的压入顺序,序列4,5,3,2,1是该压栈序列对应的一个弹出序列,但4,3,5,1,2就不可能是该压栈序列的弹出序列。
// (注意:这两个序列的长度是相等的)
function IsPopOrder(pushV, popV) {
let stack = [],k = 0;
for(let i = 0;i < pushV.length;i++){
stack.unshift(pushV[i]);
while(stack[0] && popV[k] && stack[0] === popV[k]){
stack.shift();
k++;
}
}
return stack.length === 0;
}
数组中的第K个最大元素
// 优先队列。。写的有点蛋疼
var findKthLargest = function(nums, k) {
let queue = [];
for(let i = 0;i < nums.length;i++){
if(queue.length < k) {
let pos = 0;
while(pos < k) {
if(queue[pos] === undefined) {
queue[pos] = nums[i];
break;
} else {
if(nums[i] > queue[pos]) {
queue.splice(pos,0,nums[i]);
break;
}
}
pos++;
}
} else {
if(nums[i] > queue[k-1]) {
let pos = 0;
while(pos < k) {
if(nums[i] > queue[pos]) {
queue.splice(pos,0,nums[i]);
queue.pop();
break;
}
pos++;
}
}
}
}
return queue[k-1];
};
链表
反转链表
function ReverseList(pHead) {
// write code here
if(pHead === null || pHead.next === null) return pHead;
let pre = null,nex = null;
while(pHead !== null){
nex = pHead.next;
pHead.next = pre;
pre = pHead;
pHead = nex;
}
return pre;
}
复杂链表的复制
请实现一个函数,复制一个复杂链表。在复杂链表中,每个节点除了有一个 next 指针指向下一个节点,还有一个 random 指针指向链表中的任意节点或者 null。
function Clone(pHead) {
// write code here
if(pHead === null) return pHead;
let p1 = pHead;
while(p1 !== null){
let node = new RandomListNode(p1.label);
node.next = p1.next;
p1.next = node;
p1 = node.next;
}
p1 = pHead;
while(p1 !== null){
let node = p1.next;
if(p1.random) node.random = p1.random.next;
p1 = node.next;
}
p1 = pHead;
let p2 = pHead.next;
while(p1.next !== null){
let node = p1.next;
p1.next = node.next;
p1 = node;
}
return p2;
}
合并两个有序链表
将两个升序链表合并为一个新的升序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的
var mergeTwoLists = function(l1, l2) {
if(!l1) return l2;
if(!l2) return l1;
if(!l1 && !l2) return null;
if(l1.val <= l2.val){
l1.next = mergeTwoLists(l1.next,l2);
return l1;
}else{
l2.next = mergeTwoLists(l1,l2.next);
return l2;
}
};
环形链表
给定一个链表,判断链表中是否有环
var hasCycle = function(head) {
if(!head || !head.next || !head.next.next) return false;
let fast = head.next.next,slow = head.next;
while(fast !== slow){
if(fast === null || fast.next === null) return false;
fast = fast.next.next;
slow = slow.next;
}
return true;
};
环形链表 II
给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 null
var detectCycle = function(head) {
if(!head || !head.next) return null;
let fast = head.next.next,slow = head.next,p1 = head;
while(fast !== null && fast !== slow){
if(fast.next) fast = fast.next.next;
else fast = null;
slow = slow.next;
}
if(fast === null) return null;
else{
while(p1 !== slow){
p1 = p1.next;
slow = slow.next;
}
return slow;
}
};
相交链表
编写一个程序,找到两个单链表相交的起始节点
var getIntersectionNode = function(headA, headB) {
var pA = headA;
var pB = headB;
while(pA !== pB){
pB = pB? pB.next: headA;
pA = pA? pA.next: headB;
}
return pA;
};
复制带随机指针的链表
给定一个链表,每个节点包含一个额外增加的随机指针,该指针可以指向链表中的任何节点或空节点
var copyRandomList = function(pHead) {
if(pHead === null) return pHead;
let p1 = pHead;
while(p1 !== null){
let node = new Node(p1.val);
node.next = p1.next;
p1.next = node;
p1 = node.next;
}
p1 = pHead;
while(p1 !== null){
let node = p1.next;
if(p1.random) node.random = p1.random.next;
p1 = node.next;
}
p1 = pHead;
let p2 = pHead.next;
while(p1.next !== null){
let node = p1.next;
p1.next = node.next;
p1 = node;
}
return p2;
};
字符串
电话号码的字母组合
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。

// 这个回溯可以说很巧妙了,lc上有详解
var letterCombinations = function(digits) {
if(!digits) return [];
let map = {
'2': 'abc','3':'def','4':'ghi','5':'jkl','6':'mno','7':'pqrs','8':'tuv','9':'wxyz'
};
let res = [];
function dfs(index,path) {
if(index === digits.length) {
res.push(path);
return;
}
for (let i = 0;i < map[digits[index]].length;i++) {
path += map[digits[index]][i];
dfs(index+1,path.slice());
path = path.slice(0, path.length-1);
}
}
dfs(0,'');
return res;
};
回文子串
给定一个字符串,你的任务是计算这个字符串中有多少个回文子串。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被计为是不同的子串。
var countSubstrings = function(s) {
let s2 = s.split('').reverse().join('');
let sum = 0;
const len = s.length;
for (let i = 0; i < len; i++) {
for (let j = i + 1; j <= len; j++) {
if (s.substr(i, j - i) === s2.substr(len - j, j - i)) {
sum += 1
}
}
}
return sum;
};
括号生成
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合
var generateParenthesis = function(n) {
if(!n) return [];
let res = [];
function dfs(subs,left,right,n){
if(left === n && right === n){
res.push(subs);
return;
}
if(left < right){
return;
}
left < n && dfs(subs+'(',left+1,right,n);
right < n && dfs(subs+')',left,right+1,n);
}
dfs('',0,0,n);
return res;
};
最长公共前缀
编写一个函数来查找字符串数组中的最长公共前缀。
如果不存在公共前缀,返回空字符串 ""
var longestCommonPrefix = function(strs) {
if(!strs.length) return '';
strs.sort();
let a = strs[0],b = strs[strs.length-1],res = '';
for(let i = 0;i < a.length;i++){
if(i < b.length && a[i] === b[i]){
res += a[i];
}else break;
}
return res;
};
密码解密
小明从老板那里拿到了一个密码表,说是如果解开密码表中的秘密,就可以升职加薪,赢取白富美,走向人生巅峰。这个密码表是一个 CSV 文件,里面的数据由数字(没有小数点)、字母组成。小明需要提取每个数据中的数字(例如 1a2b3c 提取后得到 123,提取后的数字整体看作一个十进制数),把数值为奇数的项相加,就可以解开这个秘密。请你实现一个函数 sum,帮小明完成这项工作。
function sum(input: string) {
return input.split(/[,\n]/)
.map(item => Number(item.replace(/[a-z]/ig, "")))
.filter(num => num % 2 === 1)
.reduce((a, b) => a + b)
}
解析url参数为对象
function parseUrl(url){
url = decodeURIComponent(url);
let strs = url.slice(url.indexOf('?')+1).split('&');
return strs.reduce((x,y)=>{
let key = y.split('=')[0];
let value = Object.is(Number(y.split('=')[1]),NaN) ? y.split('=')[1] : Number(y.split('=')[1]);
x[key] = value;
return x;
},{});
}
实现模板引擎
const template = 'there are ${count} ${name} on the ${place}.';
function parse(template,obj){
let reg = /\$\{((\w|_|\$)*)\}/g;
let keys = template.match(reg).map(x => x.slice(2,x.length-1));
let value = keys.map(i => obj[i] === undefined ? '' : String(obj[i]));
return template.replace(reg,()=> value.shift());
}
console.log(parse(template, {count: 2, name: 'apples', place: 'table'}, create));
//there are 2 apples on the table.
HTML任意标签字符串转成json文件
修改了之前的错误代码,整体思路如下:
- 将HTML字符串去<>,处理为一个数组
- 提取树形结构
- 将树形结构转JSON
const str1 = '<div>1<span>2<a>3</a>4</span>5<span>6<a>7</a>8<a>9</a>10</span>11</div>';
function Dom2JSON(str) {
str = str.split('<').map(x => x.split('>'));
let res = [],stack = [],temp = {},cur = {},key = 0;
// 获取树形结构
for(let i = 1;i < str.length; i++) {
if (str[i][0].indexOf('/') === -1) {
temp = {};
temp['key'] = key++;
temp['tag'] = str[i][0];
temp['value'] = str[i][1];
temp['children'] = [];
temp['parent'] = stack.length === 0 ? 0 : stack[0]['key'];
stack.unshift(temp);
} else {
cur = stack.shift();
// 当前元素为根元素时栈为空
stack.length !== 0 && (stack[0]['value'] = stack[0]['value'] + cur['value'] + str[i][1]);
res.unshift(cur);
}
}
// 使得遍历时索引与key值匹配
res = res.sort((x, y) => x['key'] - y['key']);
for (let i = res.length - 1;i > 0;i--) {
temp = {};
temp['tag'] = res[i]['tag'];
temp['value'] = res[i]['value'];
temp['children'] = res[i]['children'];
res[res[i]['parent']]['children'].unshift(temp);
}
res = res[0];
delete res['parent'];
delete res['key'];
return JSON.parse(JSON.stringify(res));
}
console.log(Dom2JSON(str1));
}
// 转换结果如下
// let res ={
// tag: "div",
// value: "1234567891011",
// children: [
// {
// tag: "span",
// value: "234",
// children: [
// {
// tag: "a",
// value: "3",
// children: [],
// }
// ],
// },
// {
// tag: "span",
// value: "678910",
// children: [
// {
// tag: "a",
// value: "7",
// children: [],
// },
// {
// tag: "a",
// value: "9",
// children: [],
// }
// ]
// }
// ]}
参考文献
今天的文章前端算法渣的救赎之路🚀分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/14007.html
