详解动态规划最长公共子序列–JavaScript实现

前面两篇我们讲解了01背包问题和最少硬币找零问题。这篇将介绍另一个经典的动态规划问题–最长公共子序列。如果没看过前两篇，可点击下面链接。

详解动态规划最少硬币找零问题–JavaScript实现

详解动态规划01背包问题–JavaScript实现

问题

给定两个字符串序列 abcadf , acbad，求这两个字符串的最长公共子序列

分析

最长公共子序列问题，有三个点需要注意

• 两个序列长度不一定相同
• 最长子序列是指，在两个字符串序列中以相同顺序出现
• 所求的子序列不需要连续

在进行填表分析之前，根据上面提到的三个点，我们可以很容易地先直接得出答案，最长公共子序列应为 acad

1. 建表

我们给两个子序列前面都加一个空字符，即

input1 = ["","a","c","b","a","d"],
input2 = ["","a","b","c","a","d","f"],

然后构建如下表格

为什么填一堆0呢？表示字符串无法匹配，你可以理解这是一种辅助的计算方式，在分析具体子序列时，不把构建的空字符纳入考虑范围。在后面也会按照前面2篇的思路，使用T[i][j]表示组合的子序列长度。

下面将从左往右，从上往下开始填表。我们在填写某一个表格的时候，只需要考虑小于等于i 和小于等于j的情况。比如我们要填写T[2][2]时，那么此时等同于求字符串 ac,ab的最长公共子序列，填写T[4][5]时，那么此时等同于求 acba，abcad的最长公共子序列长度。

如果你看过前两篇，对于这种填表应该会很熟悉。 下面基于这个表格，开始填表。

2. i =1

我们从第一行开始。

i=1 j=1：此时等同于求字符串 a和a的最长公共子序列长度，很显然结果为1。

i=1 j=2：此时等同于求字符串 a和ab的最长公共子序列长度，结果为1。

i=1 j=3：此时等同于求字符串 a和abc的最长公共子序列长度，结果为1。

只要一个序列只有一个字符，那么另一个序列无论多长，它们的最长公共子序列长度最多只能为1。所以 i=1 行剩余空格都填1。

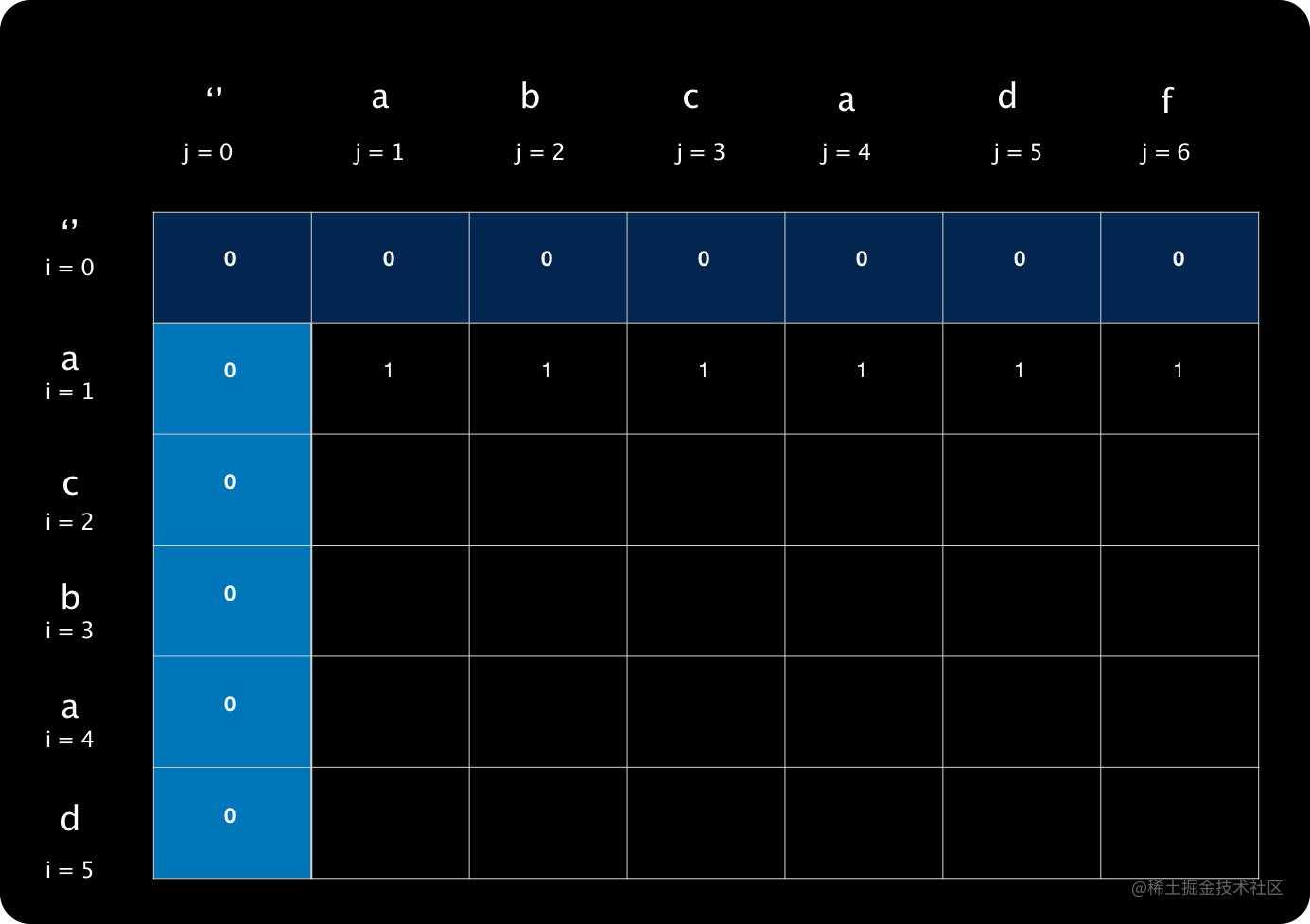
3. i = 2

i=2 j=1：此时等同于求字符串 ac和a的最长公共子序列长度，结果为1。

i=2 j=2：此时等同于求字符串 ac和ab的最长公共子序列长度，结果为1。

i=2 j=3：此时等同于求字符串 ac和abc的最长公共子序列长度。这时就有意思了。因为根据一开始的分析，求最长公共子序列时，子序列是可以不连续的，因此这两个序列的最长公共子序列应该是 ac，所以这里表格应该填2。

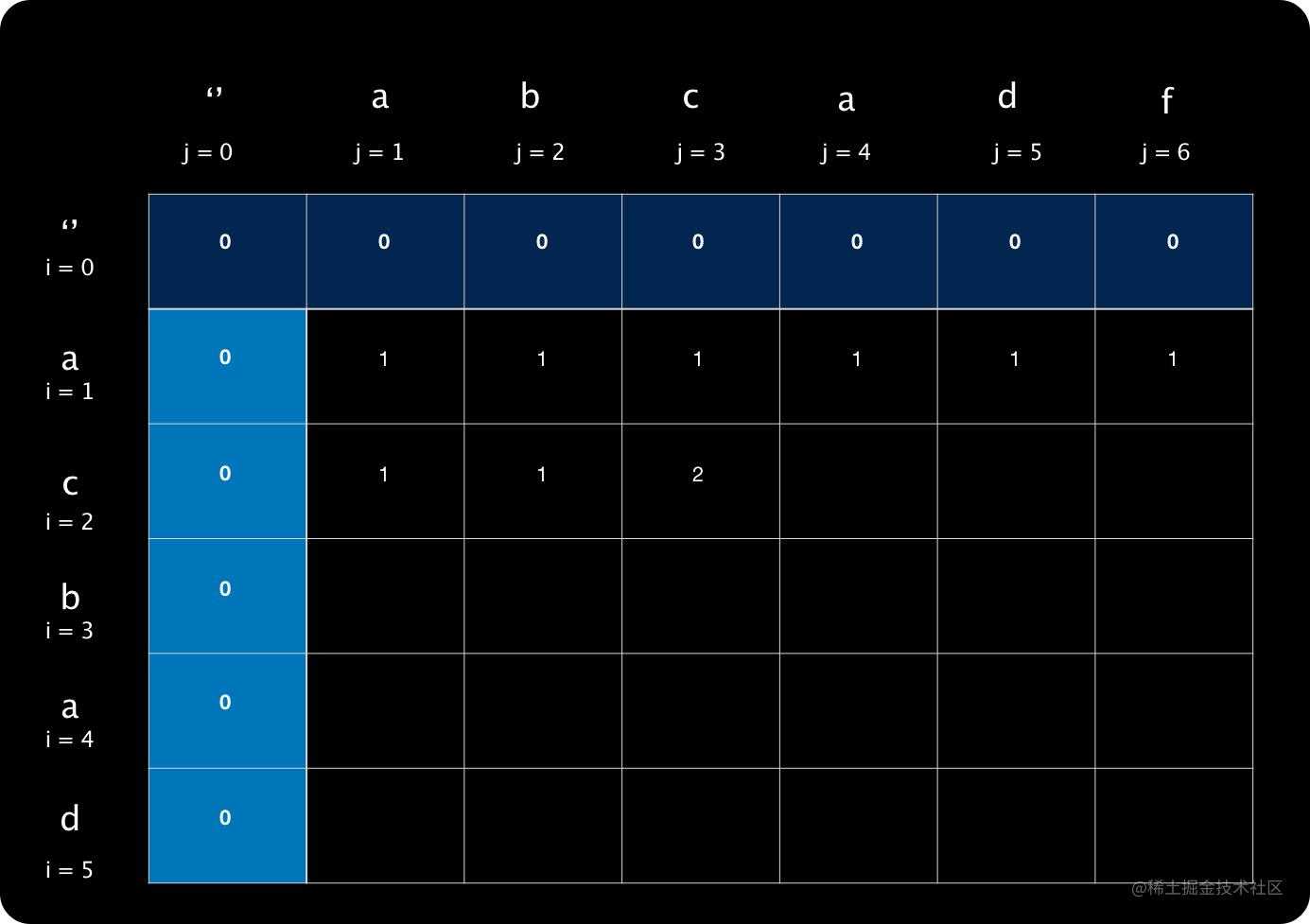
好了，停下，先不用急着继续填，我们需要先分析一下通用思路。

4.填表思路

我们从T[2][3]=2 这一个格分析。很显然去除 c 这个公共字符后，两个字符串还剩下 a, ab。是不是有点熟悉？这个其实就是填写 T[1][2] 时的组合，也就是我们可以假设当 input1[i] == input2[j]时，T[i][j]=T[i-1][j-1]+1。 当input1[i] != input2[j]时，T[i][j]的值，取它上方或左边的较大值，即[i][j] = max(T[i-1][j],T[i][j-1])。

用一句通俗的话来描述这种T[i][j]规律，就是相等左上角加一，不等取上或左最大值，如果上左一样大，优先取左。

好了，不看下面内容，你带着这种规律，把表格剩余内容自己填写完毕。

5.最终表格

理解了这种规律，我们没必要把每一格该怎么填重复叙述了。下面就是最终表格。

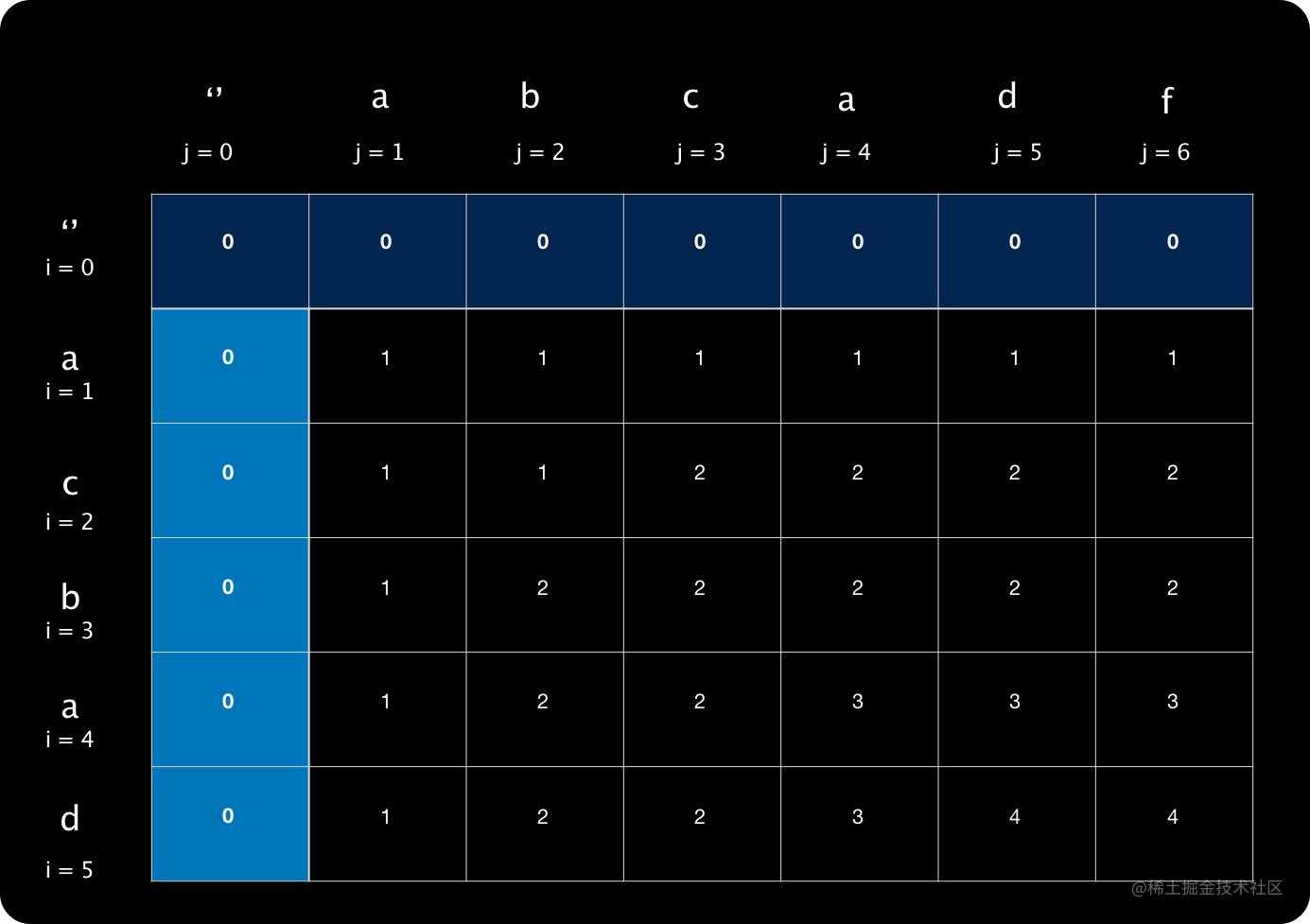
我们举个例子，比如 i=5 j=4，此时input1[i] !=input2[j]，我们取它左边（2）或者上方（3）的较大值，所以填写3。

i=5 j=5，此时input1[i] ==input2[j]，我们直接取左上角值加1，左上角的值为T[4][4]=3，所以T[5][5]=4 。

如果还不太理解，可以自己再练习画一次。

6.寻找子串

我们完成填表后，只能求出最长公共子序列的长度，但是无法得知它的具体构成。我们可以参照上一篇硬币问题，从填表的反向角度来寻找子序列。

我们子序列保存在名为 s的数组中，从表格中反向搜索，找到目标字符后，每次都把目标字符插入到数组最前面。

根据前面提供的填表口诀，我们可以反向得出寻找子序列的口诀： 如果T[i][j]来自左上角加一，则是子序列，否则向左或上回退。如果上左一样大，优先取左。

1. 从右下角开始分析，T[5][6]=4，它并不是来自左上角。它左边的值比上方大，所以它来自左边，向左回退，如下图箭头。

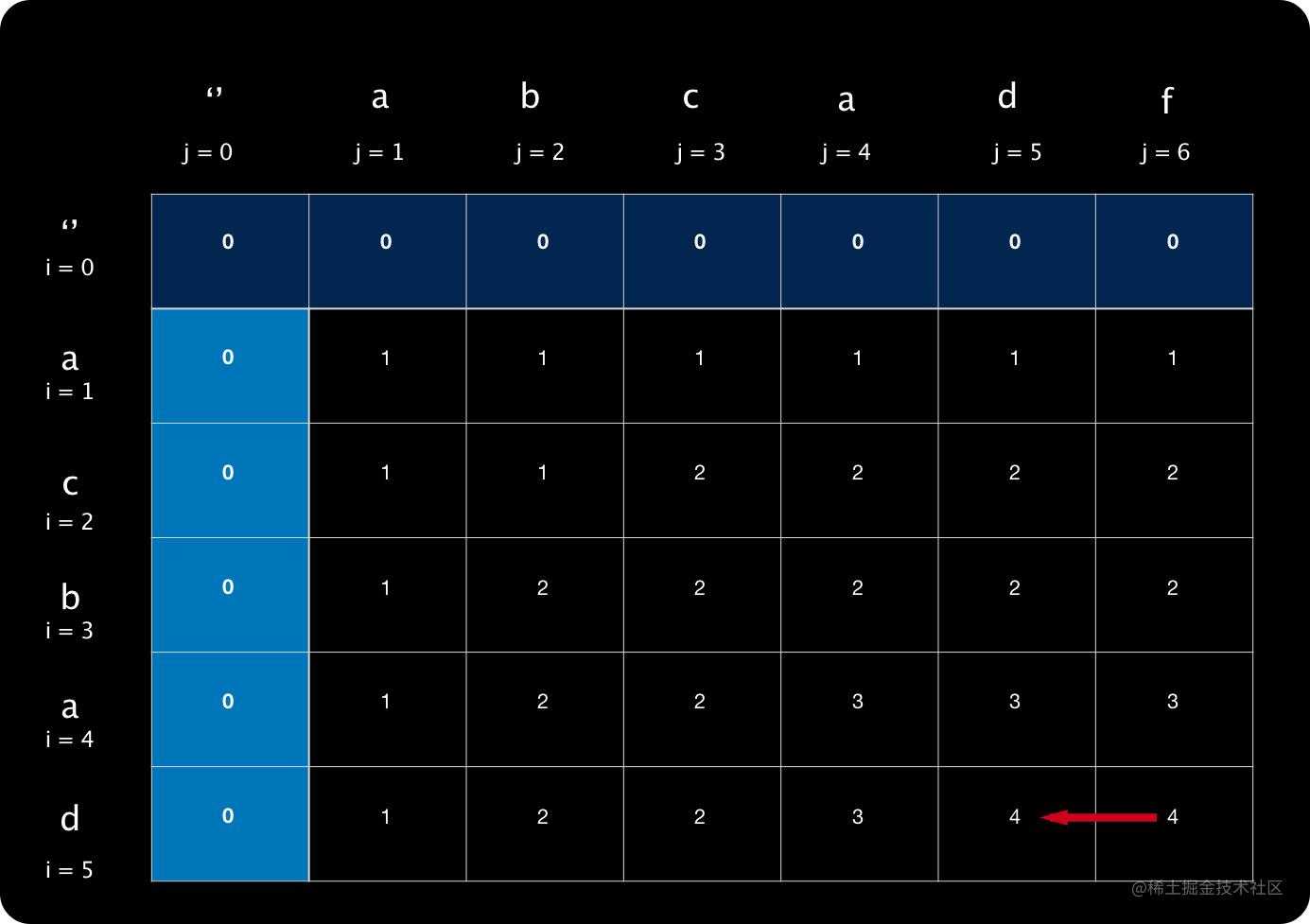
2. 接着就定位到 T[5][5]，显然他来自左上角加1，它是子序列。插入数组中，有

s = ['d']

3. 扣除掉 T[5][5]，可以定位到它的左上角 T[4][4]，如图：

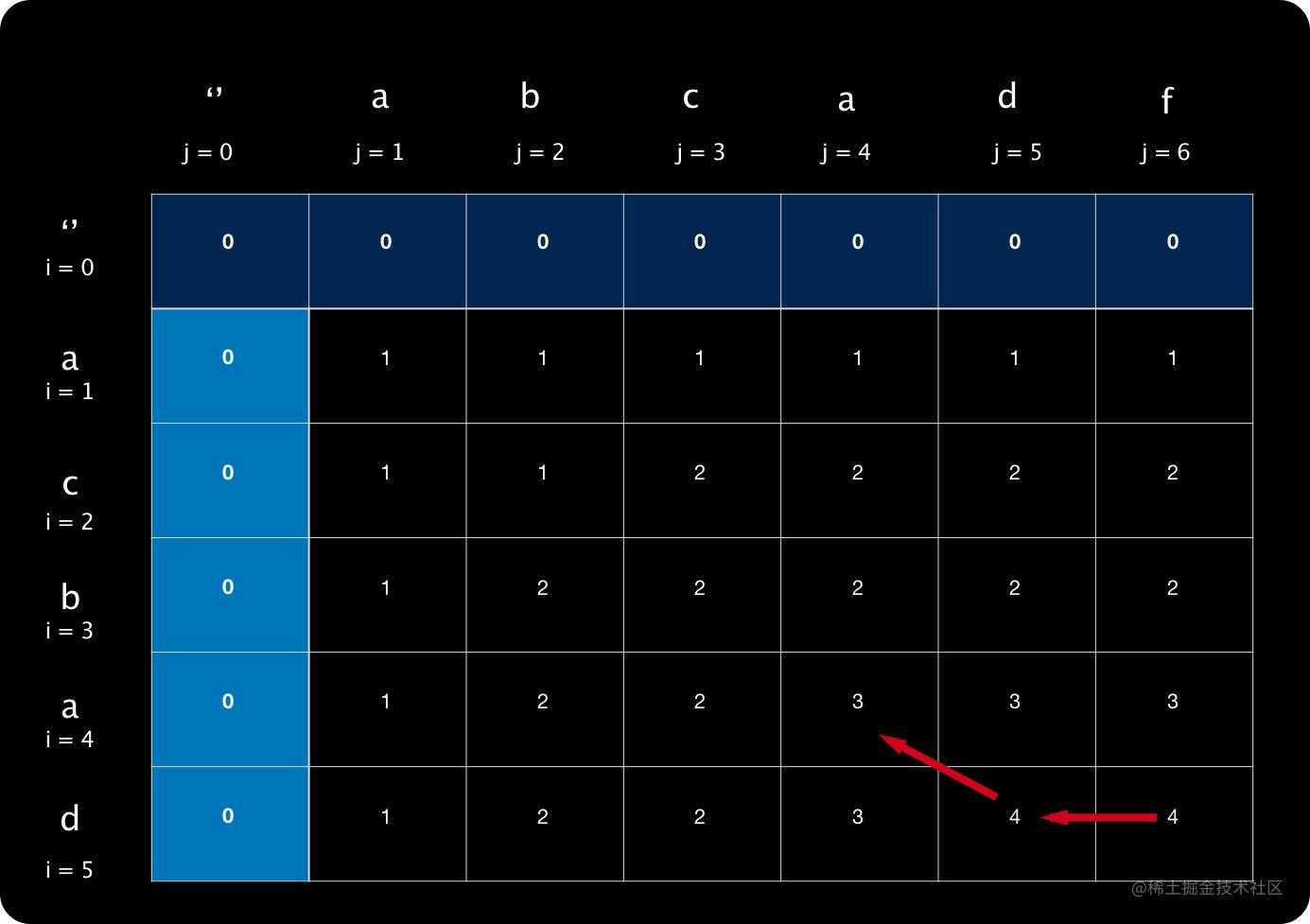
T[4][4]也是来自左上角加1，它也是子序列，把它插入到数组最前面，此时 s 应该是

s = ['a','d']

4. 按照前面的思路，继续定位分析，最终如下图：

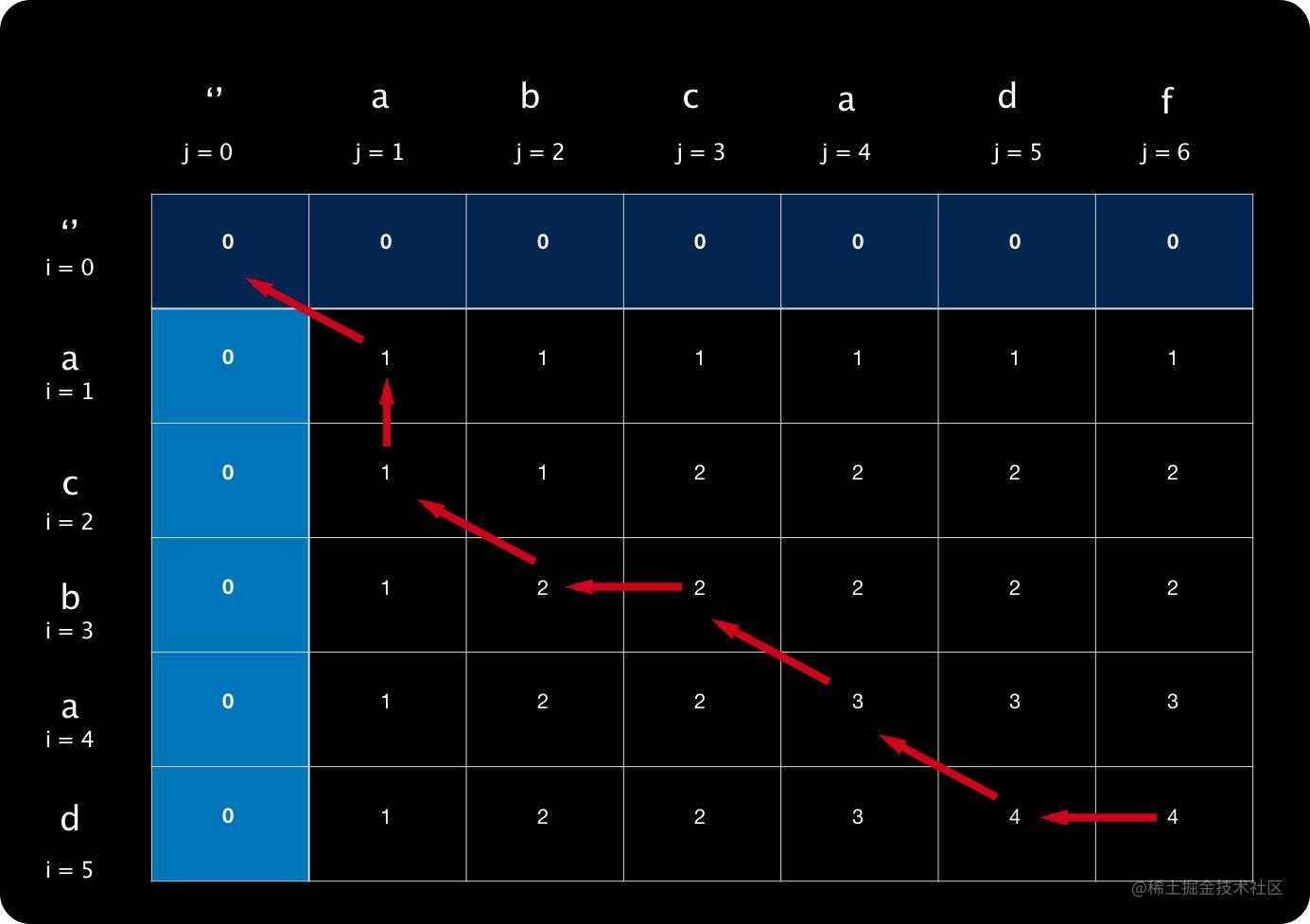
最终箭头指向0，搜索结束。

s = ['a','b','a','d']

伪代码

整个分析过程已经完成了。下面提供代码逻辑，即使不懂 JavaScript，也不会影响你理解，因为没有涉及语言特性。

填表

if(input1[i] == input2[j]){
	T[i][j] = T[i-1][j-1] + 1;
}else{
	T[i][j] = max(T[i-1][j],T[i][j-1])
}

寻找子串

if(input1[i] == input2[j]){
	s.insertToIndexZero(input1[i]); //插入到数组最前面
	i--;
	j--;
}else{
	//向左或向上回退
	if(T[i-1][j]>T[i][j-1]){
		//向上回退
		i--;
	}else{
		//向左回退
		j--;
	}
}

完整代码

最终代码使用 JavaScript 实现，如果你的 Sublime 支持纯 JavaScript，你可以直接复制黏贴代码，command + b 直接运行查看结果，然后修改输入变量，查看更多情况下的输出结果。

//动态规划 -- 最长公共子序列


//!!!!  T[i][j] 计算，记住口诀：相等左上角加一，不等取上或左最大值

function longestSeq(input1,input2,n1,n2){
	var T = []; // T[i][j]表示 公共子序列长度
	for(let i=0;i<n1;i++){
		T[i] = [];
		for(let j= 0;j<n2;j++){
			if(j==0 ||i==0){
				T[i][j] = 0;
				continue;
			}
			if(input1[i] == input2[j]){
				T[i][j] = T[i-1][j-1] + 1;
			}else{
				T[i][j] = Math.max(T[i-1][j],T[i][j-1])
			}

		}

	}

	findValue(input1,input2,n1,n2,T);

	return T;

}

//!!!如果它来自左上角加一，则是子序列，否则向左或上回退。
//findValue过程，其实就是和 就是把T[i][j]的计算反过来。
function findValue(input1,input2,n1,n2,T){
	var i = n1-1,j=n2-1;
	var result = [];//结果保存在数组中
	console.log(i);
	console.log(j);
	while(i>0 && j>0){
		if(input1[i] == input2[j]){
			result.unshift(input1[i]);
			i--;
			j--;
		}else{
			//向左或向上回退
			if(T[i-1][j]>T[i][j-1]){
				//向上回退
				i--;
			}else{
				//向左回退
				j--;
			}
		}

	}

	console.log(result);
}


//两个序列，长度不一定相等, 从计算表格考虑，把input1和input2首位都补一个用于占位的空字符串
var input2 = ["","a","b","c","a","d","f"],
	input1 = ["","a","c","b","a","d"],
	n1 = input1.length,
	n2 = input2.length;

console.log(longestSeq(input1,input2,n1,n2));