程序员的数学笔记3–迭代法

第三节课程，介绍的是迭代法。

前两节笔记的文章：

• 程序员的数学笔记1–进制转换
• 程序员的数学笔记2–余数

03 迭代法

什么是迭代法

迭代法，简单来说，其实就是不断地用旧的变量值，递推计算新的变量值。

这里采用一个故事来介绍什么是迭代法，这个故事是讲述一个国王要重赏一个做出巨大贡献的臣子，让臣子提出他想得到的赏赐，这个聪明的臣子说出了他想得到的赏赐–在棋盘上放满麦子，但要求是每个格子的麦子数量都是前一个格子的两倍。国王本以为这个赏赐可以轻而易举的满足，但真正开始放麦子后，发现即便是拿出全国的粮食也无法满足的臣子的这个赏赐。

这里我们可以用f(n)表示当前各自的麦子数量，而前一个格子的麦子数量就是f(n-1)，那么臣子的要求就可以这么表示：

f(n) = f(n-1) * 2
f(1) = 1

这也就是迭代法了，而如果用编程来实现，其实就是实现一个循环运算的过程。

用 Python 实现这个计算麦子的代码如下所示：

def get_number_of_wheat(grid):
    ''' \计算放到给定格子数量需要的麦子数量 :param grid: 格子数 :return: '''
    # f(1) = 1
    wheat_numbers = 1

    sums = wheat_numbers
    for i in range(2, grid+1):
        wheat_numbers *= 2
        sums += wheat_numbers

    print('when grid = %d, wheats numbers = %d' % (grid, sums))

    return sums

简单的测试例子：

if __name__ == '__main__':
    print('compute numbers of wheat!')
    numbers_grid = 63
    get_number_of_wheat(numbers_grid)
    print('finish')

给定格子数量是 63 个，输出结果如下：

compute numbers of wheat!
when grid = 63, wheats numbers = 9223372036854775807
finish

所以这个天文数字是 19 位数–9223372036854775807，真的是非常的多！假设一袋 50 斤的麦子估计有 130 万粒麦子，那么这个计算结果是相当于 70949 亿袋 50 斤的麦子！

迭代法的应用

看完上述例子，相信应该对迭代法的基本概念比较了解了，而迭代法的基本步骤也很简单，分为三个步骤：

• 确定用于迭代的变量。上述例子中，这个迭代变量就是f(n)和f(n-1)
• 建立迭代变量之间的递推关系。上述例子中，这个递归关系是f(n)=f(n-1)*2
• 控制迭代的过程。这里需要确定迭代的初始条件和终止条件，上述例子，初始条件就是f(1)=1，而终止条件就是达到给定的格子数了。

那么迭代法有什么应用呢？

其实，它在数学和计算机领域都有很广泛的应用，如：

• 求数值的精确或者近似解。典型的方法包括二分法（Bisection method)和牛顿迭代法(Newton’s method)；
• 在一定范围内查找目标值。典型方法包括二分查找，其实也是二分法在搜索方面的应用；
• 机器学习算法中的迭代。比如 Kmeans 聚类算法（不断迭代来对数据进行聚类）、马尔科夫链(Markov chain)、梯度下降法（Gradient descent）等。迭代法在机器学习中有广泛的应用，其实是因为机器学习的过程，就是根据已知数据和一定的假设，求一个局部最优解。迭代法可以帮助学习算法逐步搜索，直到发现这种解。

接下来会重点介绍求数值的解和查找匹配记录，这两个应用其实都是采用二分法来实现。

求方程的精确或者近似解

迭代法除了用于计算庞大的数字，还可以帮助我们进行无穷次地逼近，求得方程的精确或者近似解。

举个例子，我们要计算一个给定的正整数n（n>1)的平方根，并且不能采用编程语言自带的函数，应该如何计算呢？

首先我们可以明确的是，对于给定的正整数n，它的平方根肯定是小于它，但大于1，也就是这个平方根的取值范围是 1 到 n ，在这个范围内求一个数值的平方等于n。

这里就可以通过采用刚刚说的二分法。每次查看区间内的中间值，检查它是否符合标准。

比如我们要求 10 的平方根，寻找的区间就是[1,10]，第一个中间值就是(1+10)/2=11/2=5.5，而 5.5 的平方等于 30.25，明显比 10 大，所以寻找区间变成 5.5 的左侧，也就是[1, 5.5]，中间值就是 3.25，但 3.25 的平方是 10.5625，依然大于 10，寻找区间变为[1, 3.25]，中间值变为 2.125, 2.125 的平方是 4.515625，小于 10，所以区间就是[2.125, 3.25]，这样继续寻找和计算中间值的平方，直到发现某个数的平方正好是 10。

具体步骤如下图：

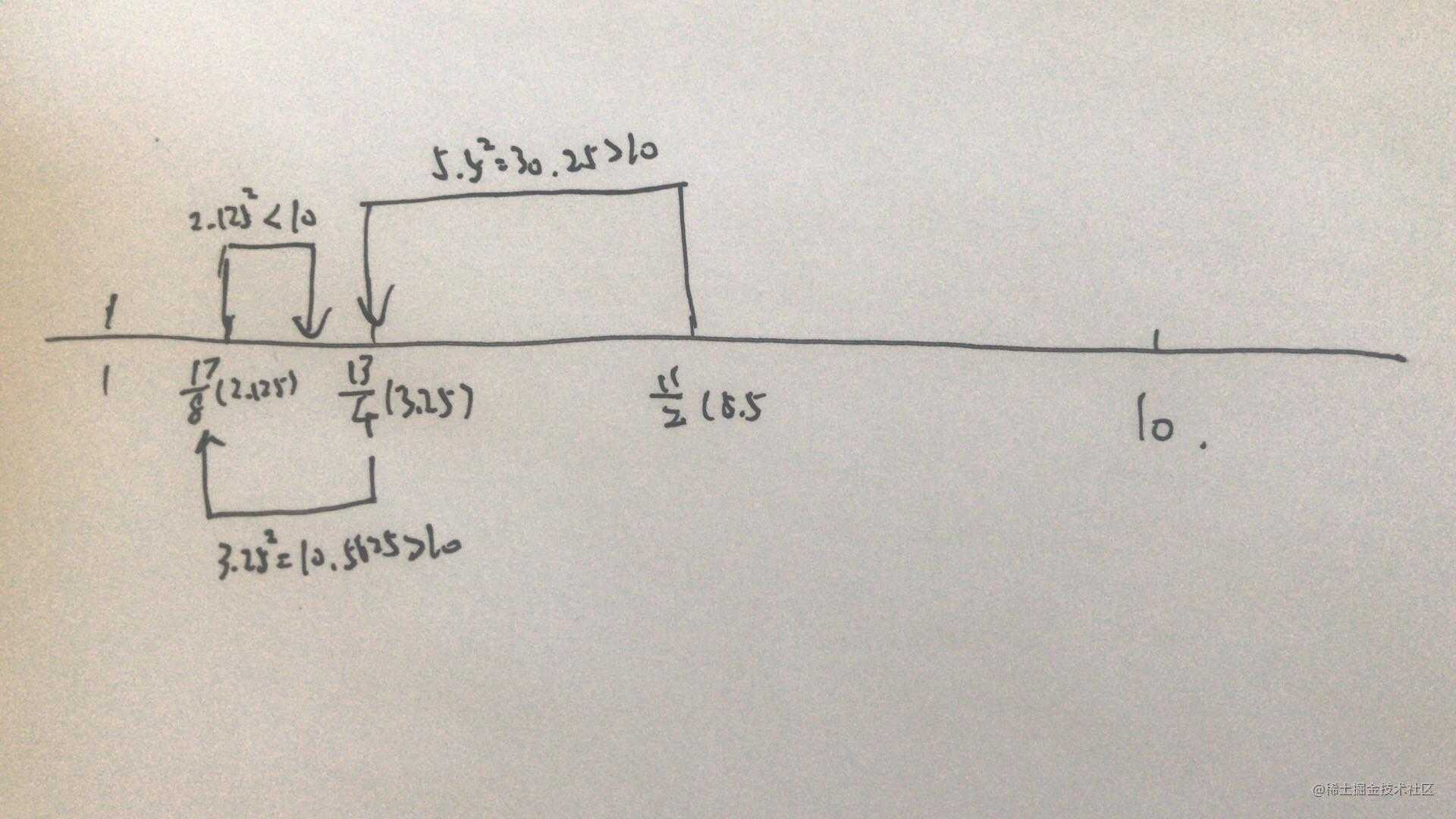
这里用代码实现，如下图所示：

def get_square_root(n, threshold, max_try):
    ''' 计算大于 1 的正整数的平方根 :param n: 给定正整数 :param threshold: 误差的阈值 :param max_try: 最大尝试次数 :return: '''
    if n <= 1:
        return -1.0
    # interval boundary 区间的左右边界
    left = 1.0
    right = float(n)
    for idx in range(max_try):
        # 防止溢出
        middle = left + (right - left) / 2
        square = middle * middle
        # 误差
        delta = abs(square / n - 1)
        if delta <= threshold:
            return middle
        else:
            if square > n:
                right = middle
            else:
                left = middle

    return -2.0

简单的测试例子：

square_root = get_square_root(10, 0.000001, 10000)
if square_root == -1.0:
    print('please input a number > 1')
elif square_root == -2.0:
    print('cannot find the square root')
else:
    print('square root==', square_root)

输出结果是：

square root== 3.1622767448425293

这里代码中，设置了两个控制迭代结束的参数：

1. threshold：误差的阈值，用于控制解的精度。理论上二分法可以通过无限次迭代求到精确解，但实际应用还需要考虑时间和计算资源，所以一般我们只需要一个近似解，而不需要完全精确的数据；
2. max_try：控制迭代的次数。设置这个参数也是为了避免使用while True循环可能导致的死循环，当然理论上设置了threshold是可以避免死循环的，但这是一个良好的编程习惯，主动避免产生的可能性。

查找匹配记录

二分法通过迭代式逼近，不仅可以求得方程的近似解，还可以帮助查找匹配的记录。

这里老师给的例子是在自然语言处理中，处理同义词或者近义词的扩展问题。这时，你是会有一个词典，用于记录每个单词的同义词或者近义词。对于一个待查找单词，我们需要在字典找到这个单词，以及对应的所有同义词和近义词，然后进行拓展，例如对于单词–西红柿，它的同义词包括了番茄和tomato。

词典如下表格所示：

当处理文章的时候，遇到“西红柿”这个单词，就在字典里查找，返回“番茄”和“tomato”等同义词或者近义词，并添加到文章作为同义词/近义词的拓展。

这里要解决的问题就是如何在字典查询匹配单词的问题。一种做法就是哈希表。而如果不用哈希表的方法，还可以采用二分查找法。二分查找法进行字典查询的思路如下：

1. 对整个字典先进行排序（假设是从小到大）。二分法的一个关键前提条件就是所查找区间必须是有序的，这样每次折半的时候，可以知道是往左还是右继续查找。
2. 使用二分法逐步定位到被查找的单词。同样是每次都选择查找区间的中间值，判断是否和待查找单词一致，如果一致就返回；如果不一致，就进行判断大小，如果比待查找单词小，就需要往中间值右边区间查找；否则就在左边区间查找。
3. 重复第二步操作，迭代式查找，直到找到单词，或者没有找到，就返回不存在。

相比于利用二分法查找方程解，二分查找必须要求数据是有序的！

用代码实现如下：

def search_word(dictionary, word):
    ''' 查找匹配单词 :param dictionary: 排序后的字典 :param word:待查找单词 :return: '''
    if dictionary is None:
        return False
    if len(dictionary) < 1:
        return False

    left = 0
    right = len(dictionary) - 1
    while left <= right:
        middle = int(left + (right - left) / 2)
        if dictionary[middle] == word:
            return True
        else:
            if dictionary[middle] > word:
                right = middle - 1
            else:
                left = middle + 1

    return False

简单的测试代码：

print('find word in dictionary')
dict_list = ['i', 'am', 'coder']
dict_list = sorted(dict_list)
print('sorted dict:', dict_list)
word_to_find = 'am'
found = search_word(dict_list, word_to_find)
if found:
    print('word "%s" found in dictionary--%s!' % (word_to_find, dict_list))
else:
    print('cannot find the word "%s"' % word_to_find)

输出结果：

find word in dictionary
sorted dict: ['am', 'coder', 'i']
word "am" found in dictionary--['am', 'coder', 'i']!
finish

迭代法的介绍就到这里了！上述源代码地址：

github.com/ccc013/Code…

欢迎关注我的微信公众号–机器学习与计算机视觉，或者扫描下方的二维码，大家一起交流，学习和进步！